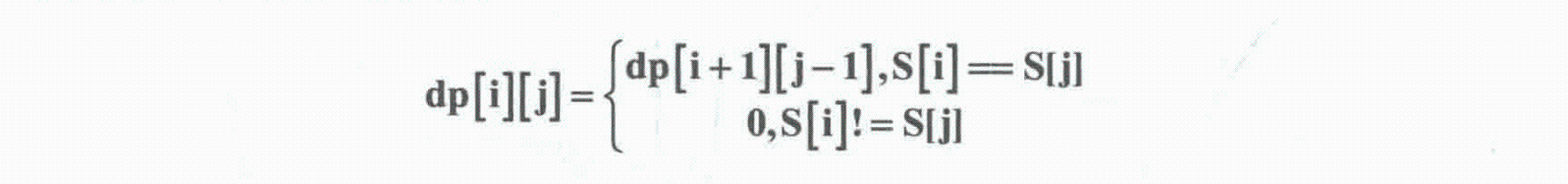最长回文子串 动态规划_leetcode最长回文子串

问题：

给出一个字符串S，求S的最长回文子串的长度。

样例

字符串"PATZJUJZTACCBCC"的最长回文子串为"ATZJUJZTA",长度为9。

        还是先看暴力解法:枚举子串的两个端点i和j,判断在[i, j]区间内的子串是否回文。从复杂度上来看，枚举端点需要0(n2),判断回文需要0(n)，因此总复杂度是O(n3)。终于碰到一个暴力复杂度不是指数级别的问题了!但是O(n)的复杂度在n很大的情况依旧不够看。
        可能会有读者想把这个问题转换为最长公共子序列(LCS) 问题来求解:把字符串S倒过来变成字符串T,然后对S和T进行LCS模型求解，得到的结果就是需要的答案。而事实上这种做法是错误的，因为一旦S中同时存在一个子串和它的倒序，那么答案就会出错。例如字符串S= “ABCDZJUDCBA”,将其倒过来之后会变成T = “ABCDUJZDCBA”,这样得到最长公共子串为”ABCD”，长度为4,而事实上S的最长回文子串长度为1。因此这样的做法是不行的。
动态规划解决
        令dp[i][j]表示S[i]至S[j]所表示的子串是否是回文子串，是则为1，不是为0。这样根据S[i]是否等于S[j]，可以把转移情况分为两类：
         ①若S[i]=S[j],那么只要S[i+1]和S[j-1]是回文子串，S[i+1]至S[j-1]就是回文子串；如果S[i+1]至S[j-1]不是回文子串，则S[i]至S[j]一定不是回文子串。
         ②若S[i]!=S[j]，那S[i]至S[j]一定不是回文子串。
由此可以写出状态转移方程

边界dp[i][i]=1,dp[i][i+1]=(S[i]==S[i+1])?1:0 。

        到这里还有一个问题没有解决,那就是如果按照i和j从小到大的顺序来枚举子串的两个端点,然后更新dp[i]lj],会无法保证dp[i + 1][ – 1]已经被计算过,从而无法得到正确的dp[i][i]。
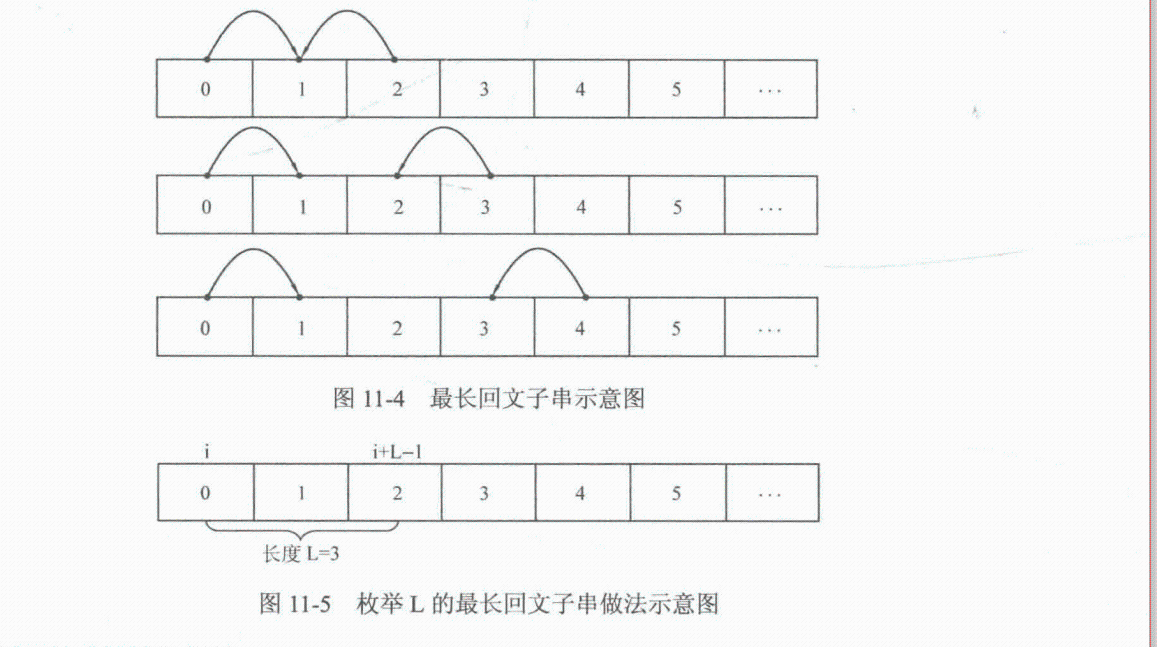
         如图11-4所示，先固定i=0,然后枚举j从2开始。当求解dp[0][2]时，将会转换为dp[1][],而dp[1][1]是在初始化中得到的;当求解dp[0][3]时,将会转换为dp[1][2], 而dp[1][2]也是在初始化中得到的;当求解dp[0][4]时，将会转换为dp[1][3], 但是dp[1][3]并不是已经计算过的值，因此无法状态转移。事实上，无论对ij和j的枚举顺序做何调整，都无法调和这个矛盾，因此必须想办法寻找新的枚举方式。
        根据递推写法从边界出发的原理，注意到边界表示的是长度为1和2的子串，且每次转移时都对子串的长度减了1,因此不妨考虑按子串的长度和子串的初始位置进行枚举，即第一遍将长度为3的子串的dp值全部求出，第二遍通过第一遍结果计算出长度为4的子串的dp值…这样就可以避免状态无法转移的问题。如图11-5所示，可以先枚举子串长度L (注意: L是可以取到整个字符串的长度S.len()的)，再枚举左端点i,这样右端点i+ L- 1也可以直接得到。

代码：

#include<iostream>
#include<string>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1000;
char S[maxn];//A存序列，dp[i]存以i为结尾的连续序列的最大和
int dp[maxn][maxn];
int main()
{
	gets(S);//从下标为1开始读入
	int len=strlen(S),ans=1;
	memset(dp,0,sizeof(dp));
	for(int i=0;i<len;i++)
	{
		dp[i][i]=1;
		if(i<len-1)
		{
			if(S[i]==S[i+1])
				{
					dp[i][i+1]=1;
					ans=2;//初始化时注意当前最长回文子串长度；
				}
		}
	}
	//状态转移方程
	for(int L=3;L<=len;L++)//枚举子串长度
		for(int i=0;i+L-1<len;i++)//枚举子串起始端点 起始端点加上子串长度(子串长度包括他
		本身，所以要-1）必须小于总长,
			{
				int j=i+L-1;//子串右端点
				if(S[i]==S[j]&&dp[i+1][j-1]==1)
				{
					dp[i][j]=1;
					ans=L;//更新最长回文子串长度;
				}
			}
		cout<<ans<<endl;
}

今天的文章最长回文子串 动态规划_leetcode最长回文子串分享到此就结束了，感谢您的阅读。