文章目录
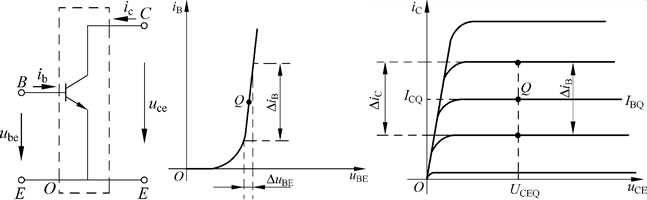
TTL门电路是三极管-三极管逻辑的简称,在数电中,我们也经常利用三极管的开关特性
在数电中,我们想让三极管工作在
截止区或者
饱和区
工作在截止区时,就有:
u B E < u o n u_{BE} < u_{on} uBE<uon,为了使三极管深度截止,我们一般令
u B E − > 0 u_{BE} -> 0 uBE−>0
工作在饱和区时:
i B ≥ i B S i_B ≥ i_{BS} iB≥iBS ->
u C E ≈ 0 u_{CE} ≈ 0 uCE≈0,我们一般令
u B E u_{BE} uBE为高电平
下面,我们先来看看三极管的开关等效电路,然后再分析其他东西:
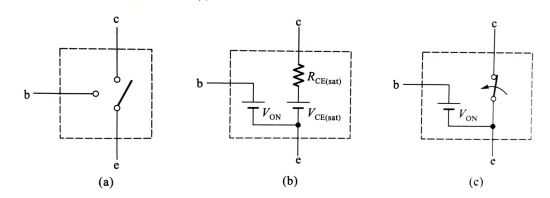
当三极管截止时,我们就可以看看(a)图,相当于开关与b, c极都不接触
当三极管饱和导通时,就是(b), (c )图,(b)图用于定量计算,(c )用于定性分析:当三极管饱和导通时,BE之间的电压就是发射结的导通电压0.7V,然后,C极和E极我们近似看成是由一个开关直接相连了(因此,在定性分析时,当三极管导通,我们认C,E等电位)
1.1 三极管反相器
接下来,我们看看三极管反相器:
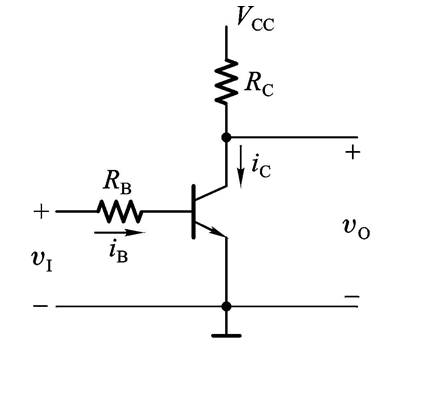
- 输入端 v I v_I vI为低电平时,三极管截止,说明 v 0 v_0 v0的电压就等于 V C C V_{CC} VCC,即输出为高电平
- 当输入端 v I v_I vI为高电平时,三极管饱和导通,BE的电压为0.7V,C,E之间相当于用开关直接连接,那么, v 0 v_0 v0 = 0V,输出为低电平
1.1.1 双极性三极管反相器的动态开关特性
1.1.2 (重要!)TTL反相器的电路结构和工作原理
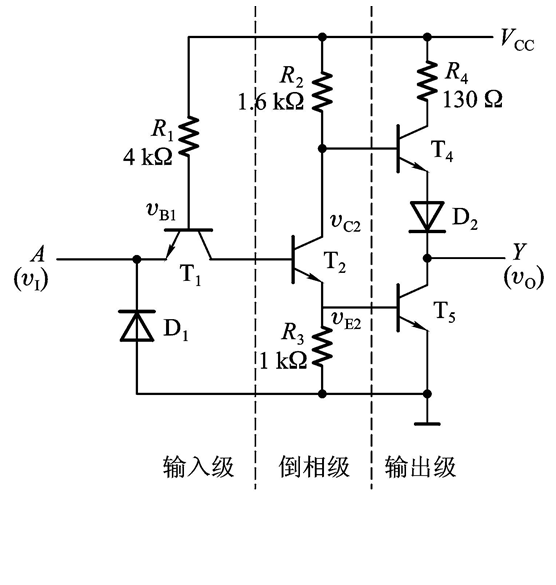
我们先来看看该电路的结构:
我们可以知道,该电路分为了输入级,倒向级还有输出级。
设电源电压 V C C V_{CC} VCC = 5V,输入信号的高,低电平分别为 V I H V_{IH} VIH = 3.4V, V I L V_{IL} VIL =
0.2V,三极管的开启电压为 V O N V_{ON} VON = 0.7V
下面我们来分析一下:
- 当输入信号 v I v_I vI为低电平0.2V时,由于T1的基极是高电平,所以T1导通了,那么由上面的分析知:T1的C,E两级相当于直接相连,那么T1的C极的电位就等于T1E极的电位等于0.2V.但是,对于T2,问题来了,T2的基极电位为0.2V,如果T2想导通,由于开启电压为0.7V,那么T2基极的电压就一定要比0.9V还要大才行,换句话说,T1的集电极电压不足以驱动T2导通,因此,T2,T5都截止,又由于T4的基极是高电位,因此,T4导通,那么, v 0 v_0 v0即输出为高电平
- 当输入信号 v I v_I vI为高电平3.4V时,由于一开始T1的基极是直接和 V C C V_{CC} VCC相连的,因此,在一开始的阶段T1的基极电位还是会高于T1的发射极电位的,所以现在T1暂时导通,那么所以T1的C极电位就等于3.4V,3.4V是足以驱动T2,T5导通的。
但是,当T2,T5导通之后,T2,T5的BE之间的电压都等于了0.7V,这就导致T1集电极的电位被钳在了1.4V,因此,T1反向导通(大家还记得三极管工作时集电结,也就是BC那个PN结是反偏的,原因就是C极的电压大于B极的电压,但是如果B极电压反过来大于了C极电压,就说明这个PN结正偏导通,三极管反向导通),那么此时,T1的B,C极之间的电压为0.7V,那么,T1的基极电位就被钳在了:0.7V +1.4V = 2.1V
大家有没有发现:在一开始T1的基极电压是大于发射极的,现在基极电压2.1V却小于发射极电压3.4V了,说明T1最终还是截止了!
这个是一方面,另一方面,由于T2,T5还是导通了,T2的 u C E u_{CE} uCE = 0.3V(虽然之前说在定性分析的时候可以看成C,E等电位,但现在我们要做定量计算),T5的 u B E u_{BE} uBE = 0.7V,所以,T4的基极电位就等于0.3V + 0.7V = 1.0V
但是:
T4要想导通,它的基极电压要是多大呢?假设T4导通,那么电流流过D2(0.7V),还有T5的 u C E u_{CE} uCE = 0.3V,因此T4基极的电压至少为:0.7V + 0.7V + 0.3V = 1.7V
很显然,现在T4的基极电压是达不到标准的,因此,T4截止
所以, v 0 v_0 v0输出低电平
对于上面这个电路,我们不难发现,T4和T5总有一个是截止,一个是导通的
1.1.3 电压传输特性
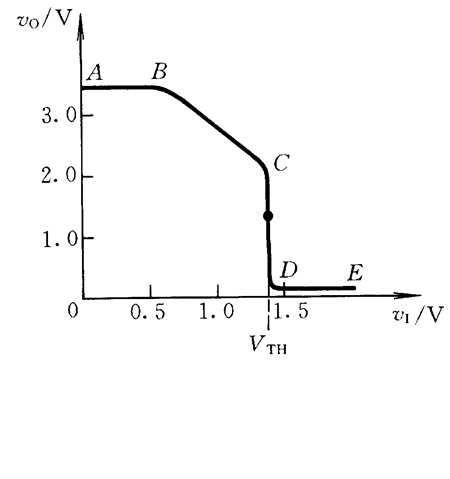
- AB段(截止区):T4导通,T2,T5截止,输出高电平
- BC段(线性区):T5截止,但T2导通,并且工作在放大区
- CD段:T4截止,T2,T5同时导通
- DE段(饱和区)
CMOS门短路的传输特性比TTL门电路的要好一些
1.1.4 TTL反相器的输入端负载特性(重要!)
对于一般的TTL门电路来说,当输入端通过负载接地时:
- 若负载≤0.7KΩ;则相当于这个输入端输入为低电平
- 若负载≥1.5KΩ;则相当于这个输入端输入为高电平
特别注意:CMOS门电路不存在这种特性!!!
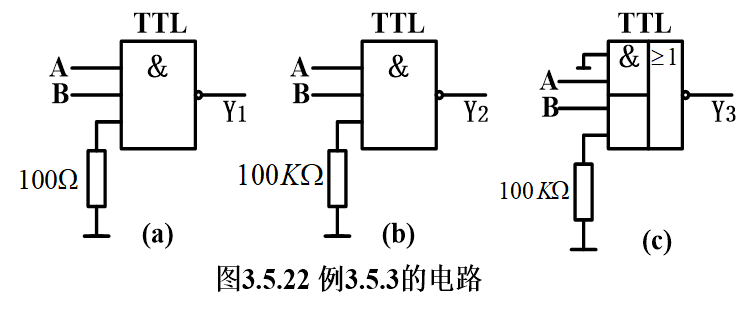
小练习:写出下面TT门电路的逻辑关系式:
Y1 = (AB0)’ = 1
Y2 = (AB1)’ = (AB)’
Y3 = ((0A)+ (B1))’ = (0 + B)’ = B’
1.2 其他类型的TTL门电路
1.2.1 TTL与非门电路
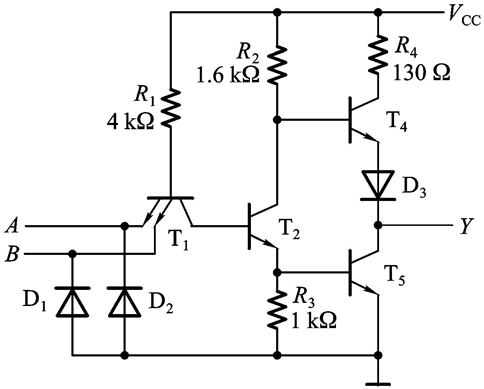
设输入的低电平电压为0.2V,输出的高电平电压为3.4V
我们来分析一下:
- 当A,B均为低电平时,T1显然导通;同时,T2B极的电位为0.2V,这将导致T2和T5均截止,又由于T4的基极为高电位,因此T4导通,输出为高电平
- 然后,我们发现:只要A和B任意一个输入为低电平,T1都会导通,然后得到一样的结果
- 最后,如果A和B均为高电平3.4V,我们来看看,由于一开始T1的基极电压还是高于3.4V的,因此在一开始,T1正向导通,那么T2基极的电位就等于3.4V,这足以驱动T2和T5导通。但是,当T2和T5导通之后,T2基极的电位就被钳在了0.7V+0.7V = 1.4V,此时,T1的基极电位高于了T1集电极的电位,因此T1反向导通,这将导致T1基极的电位被钳在了1.4V + 0.7V = 2.1V < 3.4V,最终T1截止
由于T2,T5导通,导致T4基极的电位被钳在了0.3V + 0.7V = 1V,不足以驱动T4和D3共同导通,换句话说,也即是上面的支路断了,输出低电平
因此,真值表为:
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
表示为Y = (AB)’
说明:在习题中遇到像上图这种多发射极三极管的情况,只要输入端有一个为低电平输入,那么该三极管就会导通,只有当输入全是高电平时,三极管会截止(但是注意一开始是导通的,同时注意反向导通的情况)另外,大家要记得TTL与非门的两个输入端是相关的!
1.2.3 TTL或非门电路
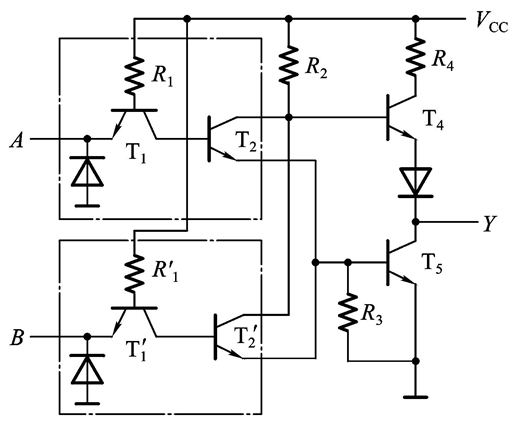
我们来分析一下:
- 当A为高电平时,B暂且不看哈:由于T1的基极和 V C C V_{CC} VCC连接,所以B极电压还是会高于A的电压,所以T1暂时导通,这就使得T2的基极电位等于3.4V,T2导通,使得T2的C和E极相通,由于T2的C极连着 V C C V_{CC} VCC,所以是高电平,因此,顺着E极传下来之后使得T5的基极电位为高电平,T5导通,输出为低电平
- 当B为高电平时,A暂且不看:同理,由于T1’的基极和 V C C V_{CC} VCC连接,所以B极电压还是会高于B的电压,所以T1’暂时导通,这就使得T2’的基极电位等于3.4V,T2’导通,由于T2‘的C极和 V C C V_{CC} VCC相连,所以导致T2’的E极也是高电平,使得T5的基极为高电平,T5导通,输出为低电平
- 当A,B同时为低电平时,T1和T1‘同时导通,使得T2的基极,T2’的基极均为低电平,T2和T2‘均截止,但是我们看到,由于T4的基极和 V C C V_{CC} VCC相连,所以T4的基极为高电平,T4导通,而T5的基极连着T2和T2’的发射极,为低电平,所以T5截止,输出为高电平
真值表为:
| A | B | Y |
|---|---|---|
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
| 0 | 0 | 1 |
逻辑表达式为Y = (A + B)’
Tips:对比上面TTL与非门来看,TTL或非门两个输入端是互不相关的
1.2.4 TTL与或非门电路
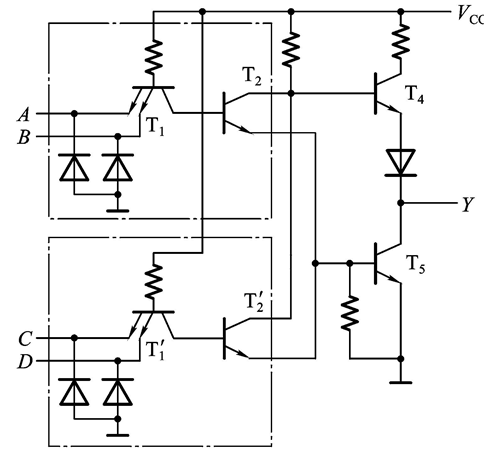
有了之前的分析基础,这一次我们不打算逐个情况的分析,而是换一种更加灵活快捷的思维去分析一下:(我们惊喜地发现这个电路的输入端和TTL与非门很接近)
我们发现A,B只要至少有一个输入是低电平,那么就会导致T1的导通,进而导致T2截止,T5截止,输出为高电平
恰巧C和D的关系也是这样
因此,只有当AB全是高电平或者CD全是低电平的情况下,T2或者T2‘才会导通,进而T5才会导通,输出低电平
那么,这就是TTL与或非门:Y = (AB + CD)’
1.2.5 TTl异或门电路
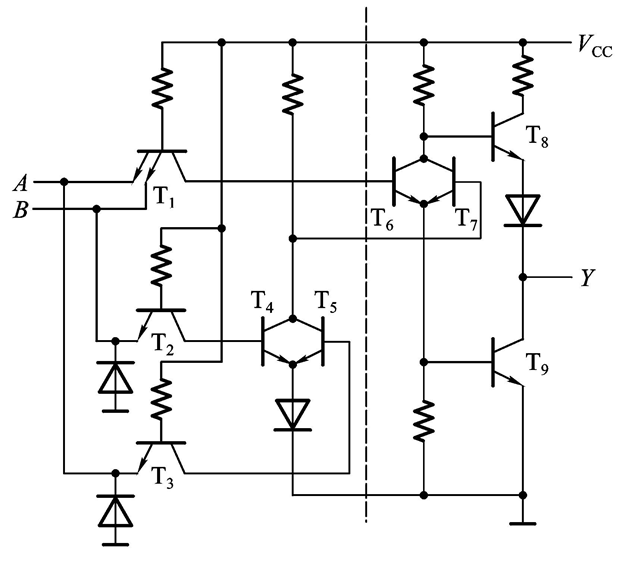
这里我们也来分析一下:我们发现输入端是一个双发射极三极管,A与B之间只要有一个是低电平,那么T1导通,我们假设A = 1,B = 0,(低电平电压为0.2V,高电平电压为3.4V)
那么此时,T3导通,导致T5基极为高电平,T5和下方二极管导通;之后T5的集电极也就是T7的基极电位就被钳位在0.3V+0.7V = 1.0V;但是1.0V的电压不足以驱动T7和T9同时导通,因此T7截止,又T1导通,T6的基极电位变为低电平,T6也截止,因此最终T9也截止,T8导通,输出高电平
A = 0,B = 1的分析类似
而当A = 1,B = 1时,T6和T9同时导通,然后使得T8的基极电位被钳位在1.0V,不足以导通T8和下面的二极管,因此,T8截止,输出低电平
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
1.2.6 集电极开路输出的门电路(OC门)
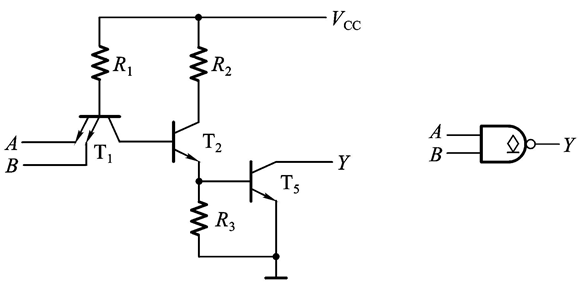
单个的OC门的逻辑功能相当于与非门,它正常工作时,需要在Y端接电源 V C C 2 V_{CC2} VCC2以及上拉电阻 R L R_L RL
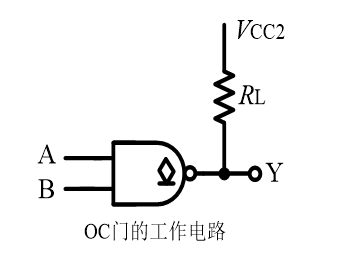
另外,多个OC门并联可以实现线与的功能:
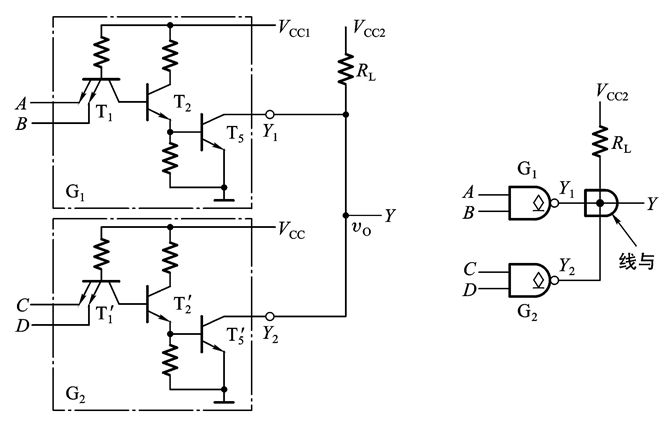
直接将输出端连起来就相当于“与”的功能
上图的逻辑表达式可以写成:Y = (AB)’(CD)’ = (AB + CD)’
下面,我们来看看上拉电阻范围的计算:
与非门在计算上拉电阻时,电流流出的数目要看与非门的数目而不是端的数目!!
在TTL门电路中计算 R L R_L RL,都是以电压作为方程的驱动:
【1】当输出为高电平时,电流的流向如下图所示:
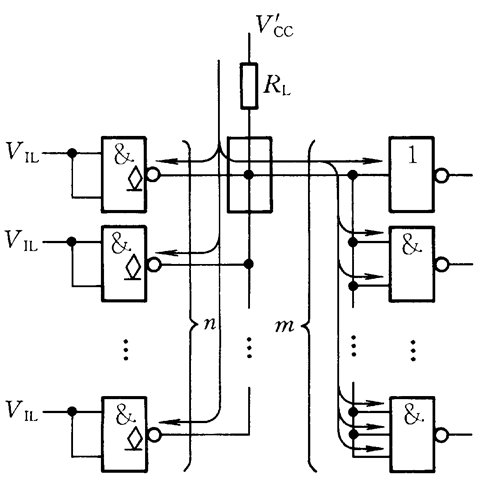
我们想要求我们输出的电压比输出高电平的最低电压还要高,因此有: V C C − R L ( n I O H + m I I H ) ≥ V O H ( m i n ) 即 R L ≤ V C C − V O H ( m i n ) n I O H + m I I H V_{CC} – R_L(nI_{OH} + mI_{IH}) ≥ V_{OH(min)}\\ 即R_L ≤ \frac{V_{CC} – V_{OH(min)}}{nI_{OH} + mI_{IH}} VCC−RL(nIOH+mIIH)≥VOH(min)即RL≤nIOH+mIIHVCC−VOH(min)
其中,n是输出端的数目,m是负载端的数目(例如一个与非门有两个输入端)
【2】输出为低电平的情况:
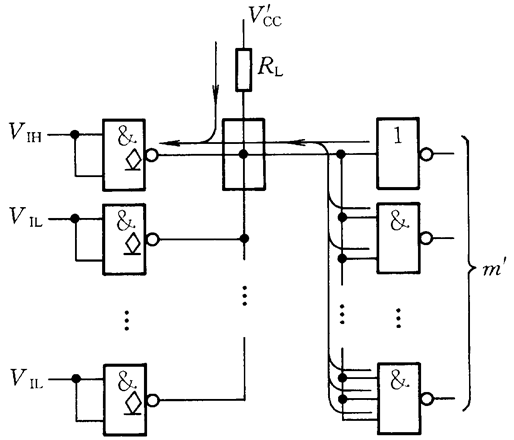
当输出为低电平时,我们想要输出的低电平比输出低电平的最高电平要小,我们考虑极端情况,假设所有电流都从一个与非门流入:
V C C − R L ( I O L − m ′ I I L ) ≤ V O L ( m i n ) 即 : R L ≥ V C C − V O L ( m i n ) I O L − m ′ I I L V_{CC} – R_L(I_{OL} – m’I_{IL}) ≤ V_{OL(min)}\\ 即:R_L ≥ \frac{V_{CC} – V_{OL(min)}}{I_{OL} – m’I_{IL}} VCC−RL(IOL−m′IIL)≤VOL(min)即:RL≥IOL−m′IILVCC−VOL(min)
特别注意:上式子中的m’是输出端与非门的个数
1.2.7 三态输出门电路(TS门)
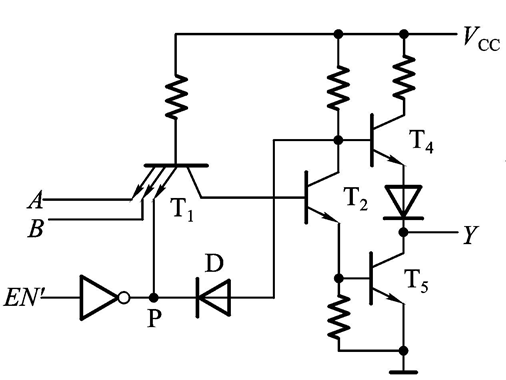
该电路的输出状态,除了高低电平外,还有一种高阻态情况
T1管只要有一个输入为低电平,那么T1就会导通。当EN’ = 1时,经过反向变成低电平0.2V,T1导通,使得T2的基极变为低电平,T2和T5截止;然后由于二极管D导通,因此T4的基极就被钳位在0.2V+0.7V = 0.9V,而0.9V不足以驱动T4和它下面的二极管同时导通,因此,T4和T5同时截止,处于高阻态状态
Tips:EN’表示该三态门是低电平有效(即EN‘为低电平时,不影响电路的正常工作状态(与非门)
EN表示三态门是高电平有效
今天的文章数字电路或门_数字电路或门「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/70508.html