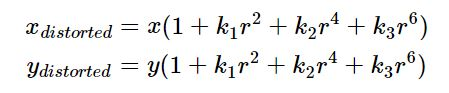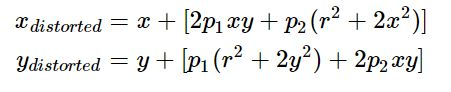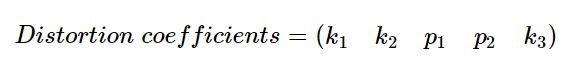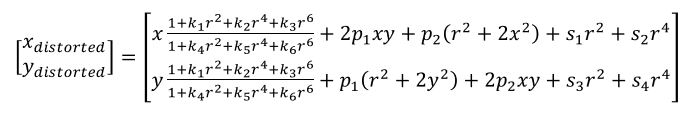双目测距 python_python编程例子「建议收藏」

一、双目测距基本流程

Stereo Vision，也叫双目立体视觉，它的研究可以帮助我们更好的理解人类的双眼是如何进行深度感知的。双目视觉在许多领域得到了应用，例如城市三维重建、3D模型构建(如kinect fusion)、视角合成、3D跟踪、机器人导航(自动驾驶)、人类运动捕捉(Microsoft Kinect)等等。双目测距也属于双目立体视觉的一个应用领域，双目测距的基本原理主要是三角测量原理，即通过视差来判定物体的远近。如果读者想对双目测距的内容有一个更加深入的认识，建议去阅读《计算机视觉中的多视图几何》，这本书是视觉领域的经典之作，它的优点是内容全面，每一个定理都给出了严格的数学证明，缺点就是理论内容非常多，而且难度也非常高，读起来更像是在看一本数学书。

那么总结起来，双目测距的大致流程就是：

双目标定 –> 立体校正（含消除畸变） –> 立体匹配 –> 视差计算 –> 深度计算(3D坐标)计算

下面将分别阐述每一个步骤并使用opencv-python来实现。本篇博客将偏重实践一些，理论方面的论述会比较少，但也会尽量写的通俗易懂。

linux下安装opencv-python：

pip install opencv-python

二、相机畸变

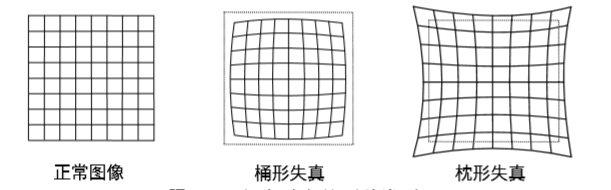
光线经过相机的光学系统往往不能按照理想的情况投射到传感器上，也就是会产生所谓的畸变。畸变有两种情况：一种是由透镜形状引起的畸变称之为径向畸变。在针孔模型中，一条直线投影到像素平面上还是一条直线。可是，在实际拍摄的照片中，摄像机的透镜往往使得真实环境中的一条直线在图片中变成了曲线。越靠近图像的边缘，这种现象越明显。由于实际加工制作的透镜往往是中心对称的，这使得不规则的畸变通常径向对称。它们主要分为两大类，桶形畸变和枕形畸变（摘自《SLAM十四讲》）如图所示：

桶形畸变是由于图像放大率随着离光轴的距离增加而减小，而枕形畸变却恰好相反。在这两种畸变中，穿过图像中心和光轴有交点的直线还能保持形状不变。

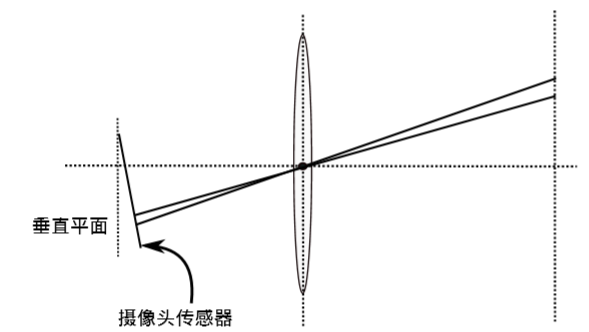
除了透镜的形状会引入径向畸变外，在相机的组装过程中由于不能使得透镜和成像面严格平行也会引入切向畸变。如图所示：

径向畸变和切向畸变一般采用多项式函数来进行建模，如下所示，

径向畸变可以建模为：

切向畸变可以建模为：

其中 $r^{2} = x^{2} + y^{2}$ ，x和y均为归一化平面坐标，按照上述建模方式，需要的畸变参数总共有5个：

通常来说有这5个畸变系数就足够了，对于某些相机来说可能还需要更高阶的参数才能够更精确地建模图像畸变，例如：

其中s1, s2, s3, s4是thin prism distortion coefficients，k4, k5, k6是径向畸变的division model。通过相机的标定可以获得以上所有的畸变参数。opencv提供了相应的函数做畸变校正, 详细介绍可以参看opencv官方文档: calib3d。

# brief: 消除畸变
# image: 输入图像
# camera_matrix: 相机内参矩阵
# dist_coeff: 相机内参矩阵
undistortion_image = cv2.undistort(image, camera_matrix, dist_coeff)

三、双目标定

双目标定的目标是获得左右两个相机的内参、外参和畸变系数，其中内参包括左右相机的fx，fy，cx，cy，外参包括左相机相对于右相机的旋转矩阵和平移向量，畸变系数包括径向畸变系数（k1， k2，k3）和切向畸变系数（p1，p2）以及其他一些畸变类型。关于双目相机的标定方法，请参考这篇博客：双目测距理论及其python实现我们可以把相机的参数存储到一个类中：

文件：stereoconfig.py

import numpy as np


# 双目相机参数
class stereoCamera(object):
    def __init__(self):
        # 左相机内参
        self.cam_matrix_left = np.array([[1499.641, 0, 1097.616],
                                                             [0., 1497.989, 772.371],
                                                              [0., 0., 1.]])
        # 右相机内参
        self.cam_matrix_right = np.array([[1494.855, 0, 1067.321],
                                                               [0., 1491.890, 777.983],
                                                               [0., 0., 1.]])

        # 左右相机畸变系数:[k1, k2, p1, p2, k3]
        self.distortion_l = np.array([[-0.1103, 0.0789, -0.0004, 0.0017, -0.0095]])
        self.distortion_r = np.array([[-0.1065, 0.0793, -0.0002,  -8.9263e-06, -0.0161]])

        # 旋转矩阵
        self.R = np.array([[0.9939, 0.0165, 0.1081],
                                     [-0.0157, 0.9998, -0.0084],
                                     [-0.1082, 0.0067, 0.9940]])

        # 平移矩阵
        self.T = np.array([[-423.716], [2.561], [21.973]])

        # 主点列坐标的差
        self.doffs = 0.0

        # 指示上述内外参是否为经过立体校正后的结果
        self.isRectified = False

    def setMiddleBurryParams(self):
        self.cam_matrix_left = np.array([[3997.684, 0, 225.0],
                                                            [0., 3997.684, 187.5],
                                                            [0., 0., 1.]])
        self.cam_matrix_right =  np.array([[3997.684, 0, 225.0],
                                                                [0., 3997.684, 187.5],
                                                                [0., 0., 1.]])
        self.distortion_l = np.zeros(shape=(5, 1), dtype=np.float64)
        self.distortion_r = np.zeros(shape=(5, 1), dtype=np.float64)
        self.R = np.identity(3, dtype= np.float64)
        self.T = np.array([[-193.001], [0.0], [0.0]])
        self.doffs = 131.111
        self.isRectified = True

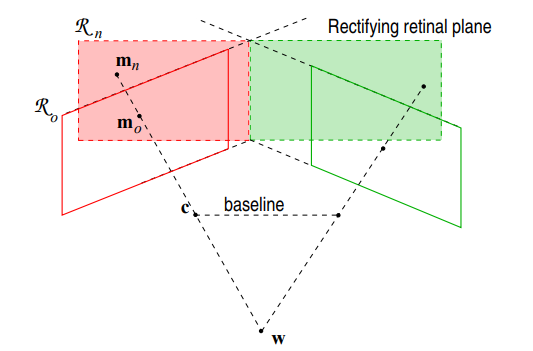
四、极线校正

极线校正的目的是将拍摄于同一场景的左右两个视图进行数学上的投影变换，使得两个图像平面共面且平行于基线，简称共面行对准。经过这样的校正过程之后，两幅图中的极线就会完全水平，从而导致空间中的同一个点在左右两幅图中的像素位置位于同一行。在达到共面行对准以后就可以应用三角原理计算距离。

OpenCV中实现了stereoRectify()函数做立体校正，函数内部采用的是Bouguet的极线校正算法，算该法需要左右相机的外参[R|T]作为输入。我们将代码封装如下，可以看到立体校正分成了两个部分：a.计算校正映射表; b.利用映射表做remap。计算校正映射表使用的是opencv函数:initUndistortRectifyMap()，该函数将极线校正和畸变校正合二为一，因此使用该函数得到的映射表对图像做处理，意味着同时完成了畸变校正和极线校正。校正完以后我们可以在校正后的图片上画上一些等间距的平行线(也就是对极线)，利用这些平行线可以辅助我们来查看一下立体校正的结果是否准确：

# 获取畸变校正和立体校正的映射变换矩阵、重投影矩阵
# @param：config是一个类，存储着双目标定的参数:config = stereoconfig.stereoCamera()
def getRectifyTransform(height, width, config):
    # 读取内参和外参
    left_K = config.cam_matrix_left
    right_K = config.cam_matrix_right
    left_distortion = config.distortion_l
    right_distortion = config.distortion_r
    R = config.R
    T = config.T

    # 计算校正变换
    height = int(height)
    width = int(width)
    R1, R2, P1, P2, Q, roi1, roi2 = cv2.stereoRectify(left_K, left_distortion, right_K, right_distortion, (width, height), R, T, alpha=0)

    map1x, map1y = cv2.initUndistortRectifyMap(left_K, left_distortion, R1, P1, (width, height), cv2.CV_32FC1)
    map2x, map2y = cv2.initUndistortRectifyMap(right_K, right_distortion, R2, P2, (width, height), cv2.CV_32FC1)

    return map1x, map1y, map2x, map2y, Q


# 畸变校正和立体校正
def rectifyImage(image1, image2, map1x, map1y, map2x, map2y):
    rectifyed_img1 = cv2.remap(image1, map1x, map1y, cv2.INTER_AREA)
    rectifyed_img2 = cv2.remap(image2, map2x, map2y, cv2.INTER_AREA)

    return rectifyed_img1, rectifyed_img2


# 立体校正检验----画线
def draw_line(image1, image2):
    # 建立输出图像
    height = max(image1.shape[0], image2.shape[0])
    width = image1.shape[1] + image2.shape[1]

    output = np.zeros((height, width, 3), dtype=np.uint8)
    output[0:image1.shape[0], 0:image1.shape[1]] = image1
    output[0:image2.shape[0], image1.shape[1]:] = image2

    # 绘制等间距平行线
    line_interval = 50  # 直线间隔：50
    for k in range(height // line_interval):
        cv2.line(output, (0, line_interval * (k + 1)), (2 * width, line_interval * (k + 1)), (0, 255, 0), thickness=2, lineType=cv2.LINE_AA)

    return output

五、立体匹配与视差图计算

立体匹配的目的是为左图中的每一个像素点在右图中找到其对应点（世界中相同的物理点），这样就可以计算出视差： $disparity = u_{l}-u_{r}$ （ $u_{l}$ 和 $u_{r}$ 分别是两个对应点在图像中的列坐标）。大部分立体匹配算法的计算过程可以分成以下几个阶段：匹配代价计算、代价聚合、视差优化、视差细化。立体匹配是立体视觉中一个很难的部分，主要困难在于：1.图像中可能存在重复纹理和弱纹理，这些区域很难匹配正确；2.由于左右相机的拍摄位置不同，图像中几乎必然存在遮挡区域，在遮挡区域，左图中有一些像素点在右图中并没有对应的点，反之亦然；3.左右相机所接收的光照情况不同；4.过度曝光区域难以匹配；5.倾斜表面、弯曲表面、非朗伯体表面；6.较高的图像噪声等。

常用的立体匹配方法基本上可以分为两类：局部方法（例如，BM、SGM、ELAS、Patch Match等）和非局部的，即全局方法（例如，Dynamic Programming、Graph Cut、Belief Propagation等）。局部方法计算量小，但匹配质量相对较低，全局方法省略了代价聚合而采用了优化能量函数的方法，匹配质量较高，但是计算量也比较大。目前OpenCV中已经实现的方法有BM、binaryBM、SGBM、binarySGBM、BM(cuda)、Bellief Propogation(cuda)、Constant Space Bellief Propogation(cuda)这几种方法。比较好用的是SGBM算法，其中匹配代价部分使用的是具有一定像素采样不变性的BT代价（原图+梯度图），并且涵盖了SGM的代价聚合方法。有关SGM算法的原理解释，可以参考另一篇博客 : 双目测距理论及其python实现

在立体匹配生成视差图之后，还可以对视差图进行滤波后处理，例如Guided Filter、Fast Global Smooth Filter、Bilatera Filter、TDSR等。视差图滤波能够将稀疏视差转变为稠密视差，并在一定程度上降低视差图噪声，改善视差图的视觉效果，但是比较依赖初始视差图的质量。

使用sgbm算法计算视差图的方法如下：

# 视差计算
def stereoMatchSGBM(left_image, right_image, down_scale=False):
    # SGBM匹配参数设置
    if left_image.ndim == 2:
        img_channels = 1
    else:
        img_channels = 3
    blockSize = 3
    paraml = {'minDisparity': 0,
             'numDisparities': 128,
             'blockSize': blockSize,
             'P1': 8 * img_channels * blockSize ** 2,
             'P2': 32 * img_channels * blockSize ** 2,
             'disp12MaxDiff': 1,
             'preFilterCap': 63,
             'uniquenessRatio': 15,
             'speckleWindowSize': 100,
             'speckleRange': 1,
             'mode': cv2.STEREO_SGBM_MODE_SGBM_3WAY
             }

    # 构建SGBM对象
    left_matcher = cv2.StereoSGBM_create(**paraml)
    paramr = paraml
    paramr['minDisparity'] = -paraml['numDisparities']
    right_matcher = cv2.StereoSGBM_create(**paramr)

    # 计算视差图
    size = (left_image.shape[1], left_image.shape[0])
    if down_scale == False:
        disparity_left = left_matcher.compute(left_image, right_image)
        disparity_right = right_matcher.compute(right_image, left_image)

    else:
        left_image_down = cv2.pyrDown(left_image)
        right_image_down = cv2.pyrDown(right_image)
        factor = left_image.shape[1] / left_image_down.shape[1]

        disparity_left_half = left_matcher.compute(left_image_down, right_image_down)
        disparity_right_half = right_matcher.compute(right_image_down, left_image_down)
        disparity_left = cv2.resize(disparity_left_half, size, interpolation=cv2.INTER_AREA)
        disparity_right = cv2.resize(disparity_right_half, size, interpolation=cv2.INTER_AREA)
        disparity_left = factor * disparity_left
        disparity_right = factor * disparity_right

    # 真实视差（因为SGBM算法得到的视差是×16的）
    trueDisp_left = disparity_left.astype(np.float32) / 16.
    trueDisp_right = disparity_right.astype(np.float32) / 16.

    return trueDisp_left, trueDisp_right

六、深度图计算

得到了视差图之后，就可以计算像素深度了，公式如下（推导略）：

$depth =\frac{ f\times b}{d + \left(c_{xr}- c_{xl}\right )}$

其中 f 为焦距长度（像素焦距），b为基线长度，d为视差， $c_{xl}$ 与 $c_{xr}$ 为两个相机主点的列坐标。

注：在opencv中使用StereoRectify()函数可以得到一个重投影矩阵Q，使用Q矩阵也可以将像素坐标转换为三维坐标。

# 利用opencv函数计算深度图
def getDepthMapWithQ(disparityMap : np.ndarray, Q : np.ndarray) -> np.ndarray:
    points_3d = cv2.reprojectImageTo3D(disparityMap, Q)
    depthMap = points_3d[:, :, 2]
    reset_index = np.where(np.logical_or(depthMap < 0.0, depthMap > 65535.0))
    depthMap[reset_index] = 0

    return depthMap.astype(np.float32)


# 根据公式计算深度图
def getDepthMapWithConfig(disparityMap : np.ndarray, config : stereoconfig.stereoCamera) -> np.ndarray:
    fb = config.cam_matrix_left[0, 0] * (-config.T[0])
    doffs = config.doffs
    depthMap = np.divide(fb, disparityMap + doffs)
    reset_index = np.where(np.logical_or(depthMap < 0.0, depthMap > 65535.0))
    depthMap[reset_index] = 0
    reset_index2 = np.where(disparityMap < 0.0)
    depthMap[reset_index2] = 0
    return depthMap.astype(np.float32)

七、双目测距的精度

根据上式可以看出，某点像素的深度精度取决于该点处估计的视差d的精度。假设视差d的误差恒定，当测量距离越远，得到的深度精度则越差，因此使用双目相机不适宜测量太远的目标。如果想要对与较远的目标能够得到较为可靠的深度，一方面需要提高相机的基线距离，但是基线距离越大，左右视图的重叠区域就会变小，内容差异变大，从而提高立体匹配的难度，另一方面可以选择更大焦距的相机，然而焦距越大，相机的视域则越小，导致离相机较近的物体的距离难以估计。

八、构建点云

有了视差便可以计算深度，因此根据双目的视差图可以构建稠密点云，OpenCV中提供了reprojectImageTo3D()这个函数用于计算像素点的三维坐标，该函数会返回一个3通道的矩阵，分别存储左相机坐标系下每个像素的(x, y, z)坐标。建议使用Open3D进行三维点云的渲染，经过近些年的发展, Open3D已经逐步变得易用，可扩展，且安装方便，在python环境下只需使用pip即可安装：

pip install open3d

pcl由于安装不太方便，不建议使用。在python-pcl库中提供了用来显示点云的工具（python-pcl是PCL库的python接口，但是只提供了部分功能，且对点云的各种处理功能只限于PointXYZ格式的点云），python-pcl的下载地址：GitHub – strawlab/python-pcl: Python bindings to the pointcloud library (pcl)，下载好后按步骤安装好。windows平台下的安装可以参考这两个博客：1.Windows10下PCL1.8.1以及Python-pcl1.81环境配置的掉发之路 2.win10平台python-pcl环境搭建

下面是构建并显示点云的代码：

# 将h×w×3数组转换为N×3的数组
def hw3ToN3(points):
    height, width = points.shape[0:2]

    points_1 = points[:, :, 0].reshape(height * width, 1)
    points_2 = points[:, :, 1].reshape(height * width, 1)
    points_3 = points[:, :, 2].reshape(height * width, 1)

    points_ = np.hstack((points_1, points_2, points_3))

    return points_


# 深度、颜色转换为点云
def DepthColor2Cloud(points_3d, colors):
    rows, cols = points_3d.shape[0:2]
    size = rows * cols

    points_ = hw3ToN3(points_3d)
    colors_ = hw3ToN3(colors).astype(np.int64)

    # 颜色信息
    blue = colors_[:, 0].reshape(size, 1)
    green = colors_[:, 1].reshape(size, 1)
    red = colors_[:, 2].reshape(size, 1)

    rgb = np.left_shift(blue, 0) + np.left_shift(green, 8) + np.left_shift(red, 16)

    # 将坐标+颜色叠加为点云数组
    pointcloud = np.hstack((points_, rgb)).astype(np.float32)

    # 删掉一些不合适的点
    X = pointcloud[:, 0]
    Y = pointcloud[:, 1]
    Z = pointcloud[:, 2]

    # 下面参数是经验性取值，需要根据实际情况调整
    remove_idx1 = np.where(Z <= 0)
    remove_idx2 = np.where(Z > 15000)  // 注意单位是mm
    remove_idx3 = np.where(X > 10000)
    remove_idx4 = np.where(X < -10000)
    remove_idx5 = np.where(Y > 10000)
    remove_idx6 = np.where(Y < -10000)
    remove_idx = np.hstack((remove_idx1[0], remove_idx2[0], remove_idx3[0], remove_idx4[0], remove_idx5[0], remove_idx6[0]))

    pointcloud_1 = np.delete(pointcloud, remove_idx, 0)


    return pointcloud_1


# 点云显示
def view_cloud(pointcloud):
    cloud = pcl.PointCloud_PointXYZRGBA()
    cloud.from_array(pointcloud)

    try:
        visual = pcl.pcl_visualization.CloudViewing()
        visual.ShowColorACloud(cloud)
        v = True
        while v:
            v = not (visual.WasStopped())
    except:
        pass

九、代码实现

最重要的就是代码了，不是么！以下是全部代码：

修改时间：2021.1.11（第一次）

修改时间：2022.1.14（添加基于库open3d的点云绘制）

comming soon ……

十、效果图

下面的数据使用的是MiddleBurry双目数据，可以不用做立体校正（因为已经校正过了）,数据下载地址：2014 Stereo Datasets：

利用SGBM算法得到视差图如下：

点云如图所示：

参考资料：

SGBM算法详解（一）

SGBM算法详解（二）

双目视觉之空间坐标计算

Stereo disparity quality problems

Disparity map post-filtering

OpenCV Stereo – Depth image generation and filtering

双目视觉测距原理，数学推导及三维重建资源

真实场景的双目立体匹配（Stereo Matching）获取深度图详解

双目测距的原理

opencvSGBM半全局立体匹配算法的研究(1)

双目测距（三）–立体匹配

OpenCV学习笔记（19）双目测距与三维重建的OpenCV实现问题集锦（四）三维重建与OpenGL显示

Open3D介绍与使用: open3d library for 3d data processing

今天的文章双目测距 python_python编程例子「建议收藏」分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/75201.html