指数平滑算法

对时间序列的预测，用的最多的是指数平滑算法，算法不复杂。

基本公式

定义和实现

首先理解一个基本公式：

　指数平滑法的基本公式是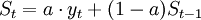： 式中，

• S_t–时间t的平滑值；
• y_t–时间t的实际值；
• S_{t − 1}–时间t-1的平滑值；
• a–平滑常数，其取值范围为(0,1)；

说明：

1. 此公式用t-1时刻的平滑值和t时刻的实际值来计算t时刻的平滑值

2. a是系数，越接近1的话，远期数据对于计算结果影响越小，越接近0,则影响越大

用newlisp表达公式如下：

(define (cal-basic real-t1 smooth-t0 a)
  (add (mul a real-t1) (mul (sub 1 a) smooth-t0)))

说明：

t0 就是 t-1

t1 就是t

newlisp stat模块

Lutz介绍，该模块的smooth函数可以用来完成基础公式的功能，使用方法如下：

> (stat:smooth '(1 5 2 6 4 7 2) 0.5)
(1 3 2.5 4.25 4.125 5.5625 3.78125)

内部代码实现和基础公式一样，只不过一次批量产生多个平滑值，这里第一个平滑值就是第一个实际值：

; expontial smoothing with 0 < alpha <= 1
(define (smooth lst alpha , previous slist)
  (set 'previous (first lst))
  (set 'slist '())
  (dolist (elmnt lst) 
   (set 'previous (add (mul alpha elmnt) (mul (sub 1 alpha) previous))) 
   (push previous slist))
  (reverse slist)) ; could be written shorter starting v.9.9.5
                   ; because push returns the modified list

预测公式

一次指数平滑预测

有了这个基本公式，我们就可以得到t1时刻的平滑值smooth-t1, 然后可以再次运用基本个公式进行预测，这个方法就叫做一次指数平滑预测

smooth-t2=a * real-t1 + (1-a) * smooth-t1

newlisp代码为：

;; @return smooth value of t2
(define (cal-exponential1 real-t1 smooth-t0 a)
  (let (smooth-t1 (cal-basic real-t1 smooth-t0 a))
    (print (add (mul a real-t1) (mul (sub 1 a) smooth-t1)))
  ))

今天的文章指数平滑算法分享到此就结束了，感谢您的阅读。