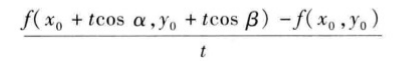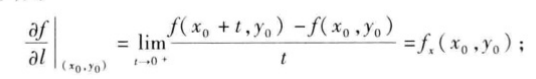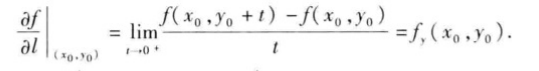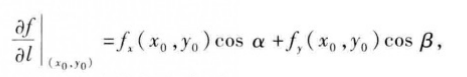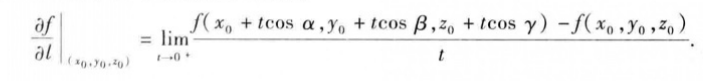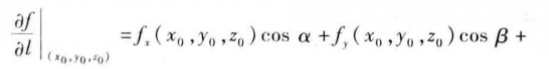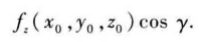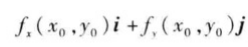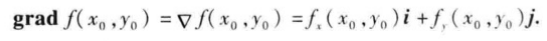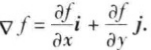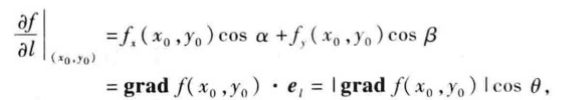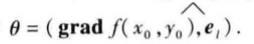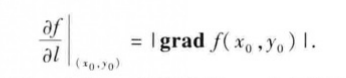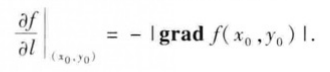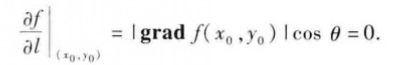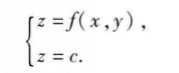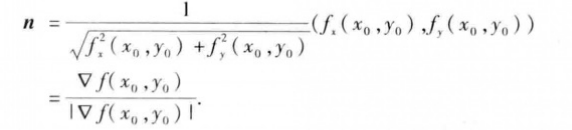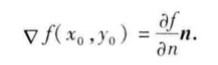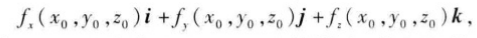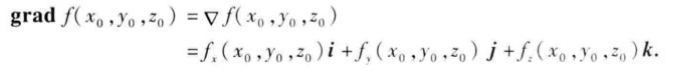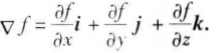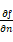1 方向导数

考虑函数沿坐标轴方向的变化率是不够的.例如，热空气要向冷的地方流动,气

象学中就要确定大气温度、气压沿着某些方向的变化率.因此我们有必要来讨论

函数沿任一指定方向的变化率问题.

1.1  方向导数定义

设 是xoy平面上以P0(x0,y0)为始点的一条射线,el=(cosα,cosβ)是与

 同方向的单位向量.射线的参数方程为

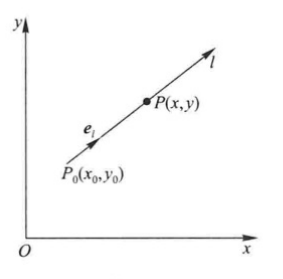
设函数z=f(x,y)在点P0(x0,y0)的某个邻域

U(P0)内有定义,P(x0+ tcosα,y0 + tcosβ)为上

另一点,且P∈U(P0)如果函数增量f(x0+tcosα,Y0 +tcosβ)-f(x0,y0)与P到P0的距离|PP0| =t

的比值

从方向导数的定义可知，方向导数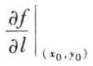 就是函数f(x,y)在点P0(x0,y0)处沿方向的变化率.若函数f(x,y)在点P0(x0,y0)的偏导数存在，e =i=(1,0)则

又若e =j=(0,1)则

 关于方向导数的存在及计算,我们有以下定理.

定理:如果函数f(x,y)在点 P0(x0,y0)可微分,那么函数在该点沿任一方

向的方向导数存在,且有

1.2 方向导数计算

1.3 三元函数方向导数

对于三元函数f(x,y,z)来说,它在空间一点P0(x0,y0,z0)沿方向 eƖ =(cosα,cosβ,cosƳ)的方向导数为

同样:如果函数f(x,y,z)在点(x0,y0,z0)可微分,那么函数在该点沿着方向eƖ =(cosα,cosβ,cosƳ)的方向导数为

2、梯度

与方向导数有关联的一个概念是函数的梯度.在二元函数的情形,设函数

f(x,y)在平面区域D内具有-阶连续偏导数,则对于每一点P0(x0,y0)∈D,都

可定出一个向量

这向量称为函数f(x,y)在点P0(x0,y0)的梯度，记作grad f(x0，y0)或

∇ f(x0,y0),即

其中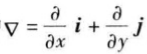 称为(二维的)向量微分算子或Nabla算子

如果函数f(x,y)在点P0(x0,y0)可微分, el=(cosα,cosβ)是与方向l同向

的单位向量,那么

其中

这一关系式表明了函数在一点的梯度与函数在这点的方向导数间的关系.特别,由这关系可知:

(1)当Ɵ=0,即方向el与梯度grad f(x0,y0)的方向相同时, 函数f(x,y)增

加最快.此时,函数在这个方向的方向导数达到最大值,这个最大值就是梯度

grad f(x0,y0)的模,即

这个结果也表示:函数f(x,y)在一点的梯度grad f是这样一个向量,它的方向

是函数在这点的方向导数取得最大值的方向,它的模就等于方向导数的最大值.

(2)当Ɵ=π,即方向el与梯度grad f(x0,y0)的方向相反时,函数f(x,y)减

少最快,函数在这个方向的方向导数达到最小值，即

(3)当Ɵ=π/2,即方向el与梯度grad f(x0,y0)的方向正交时,函数的变化率

为零,即

我们知道,一般说来二元函数z=f(x,y)在几何上表示-个曲面,这曲面被

平面z=c(c是常数)所截得的曲线L的方程为

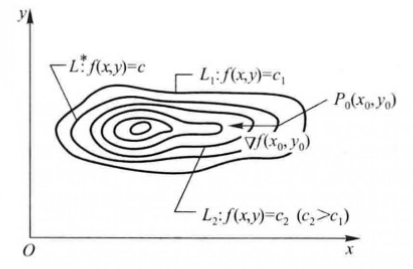
这条曲线L在xOy面上的投影是一条平面曲线L*(如图),它在xOy平

面直角坐标系中的方程为f(x,y) =c.对于曲线L*上的一切点,已给函数的

函数值都是c,所以我们称平面曲线L*为函数z=f(x,y)的等值线.若fx,fy不同时为零,则等值线f(x,y)=c.上任一点P0(x0,y0)处的一个单位法向量为

这表明函数f(x,y)在一点(x0,y0)的梯度∇ f(x0,y0)的方向就是等值线

f(x,y) =c在这点的法线方向n,而梯度的模|∇ f(x0,y0)|就是沿这个法线方向

的方向导数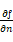 于是有

上面讨论的梯度概念可以类似地推广到三元函数的情形.设函数f(x,y,z)

在空间区域G内具有一阶连续偏导数,则对于每一点P0(x0,Y0,z0)∈G,都可定

出一个向量

这向量称为函数f(x,y,z)在点P(x0,y0,z0)的梯度,将它记作

grad f(x0,y0,z0)或∇f(x0,y0,z0),即

其中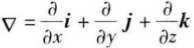 称为(三维的)向量微分算子或Nabla算子

经过与二元函数的情形完全类似的讨论可知，三元函数f(x,y,z)在一点的

梯度∇f是这样一个向量,它的方向是函数f(x,y,z)在这点的方向导数取得最大

值的方向,它的模就等于方向导数的最大值.

如果引进曲面

f(x,y,z) =c

为函数f(x,y,z)的等值面的概念,那么可得函数f(x,y,z)在一-点(x0，y0,z0)的梯度∇ f(x0,y0,z0)的方向就是等值面f(x,y,z) =c在这点的法线方向n.而梯度的模|∇ f(x0,y0,z0)|就是函数沿这个法线方向的方

向导数

2.1 梯度的计算

今天的文章方向导数和梯度分享到此就结束了，感谢您的阅读。