离散数学9：二部图、欧拉图、哈密顿图

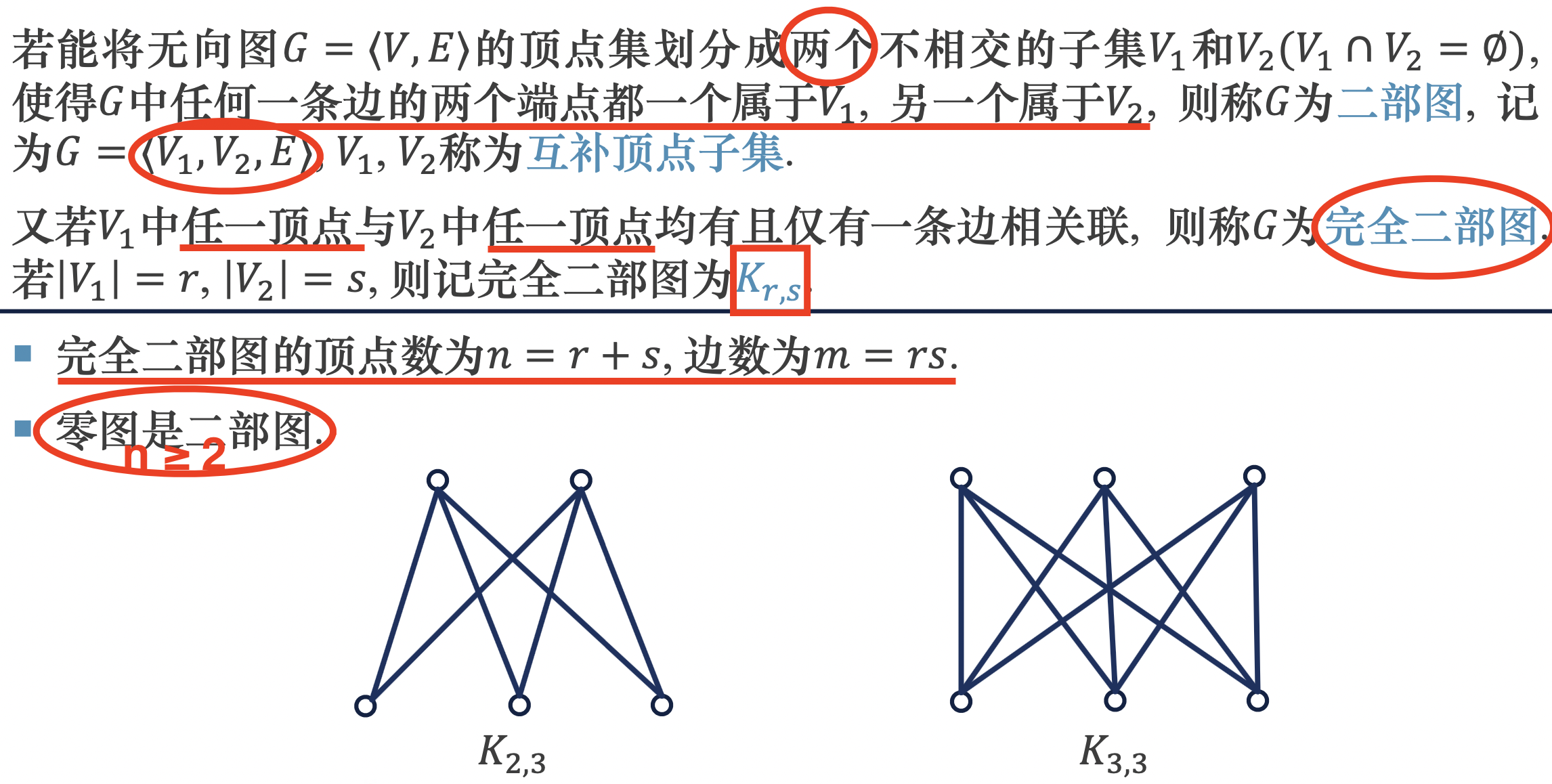
二部图

将所有边均视为沟通两个互补顶点子集的路。

若一个点集中任意2个顶点间均没有边相连，则称该点集为独立集。可见二部图的2个部都是独立集。
一个图是二部图 $⟺$ 该图的顶点集是2个独立集的并集。

含有自环的顶点不可能在独立集中，因此二部图中不能存在自环。

二部图的判定

• $一个无向图是二部图⟺图中不存在奇数长度的回路$
• 无回路的图一定是二部图

二部图的匹配

完美匹配 ${}_{\nLeftarrow }^{\Rightarrow }$ 最大匹配 ${}_{\nLeftarrow }^{\Rightarrow }$ 极大匹配
完美匹配中，$|V_1|=|V_2|=|E|$.

Hall婚姻定理——判断是否存在完备匹配
$$\begin{gathered} 设二部图G=<V_1,V_2,E>，|V_1|\le |V_2|， \\ 则G中存在完备匹配⟺V_1中任意k顶点 \end{gathered}$$至少$与V_2中的k个顶点相邻。（k=1，2，\dots ，|V_1|）$
这个条件也称为“相异性条件”。

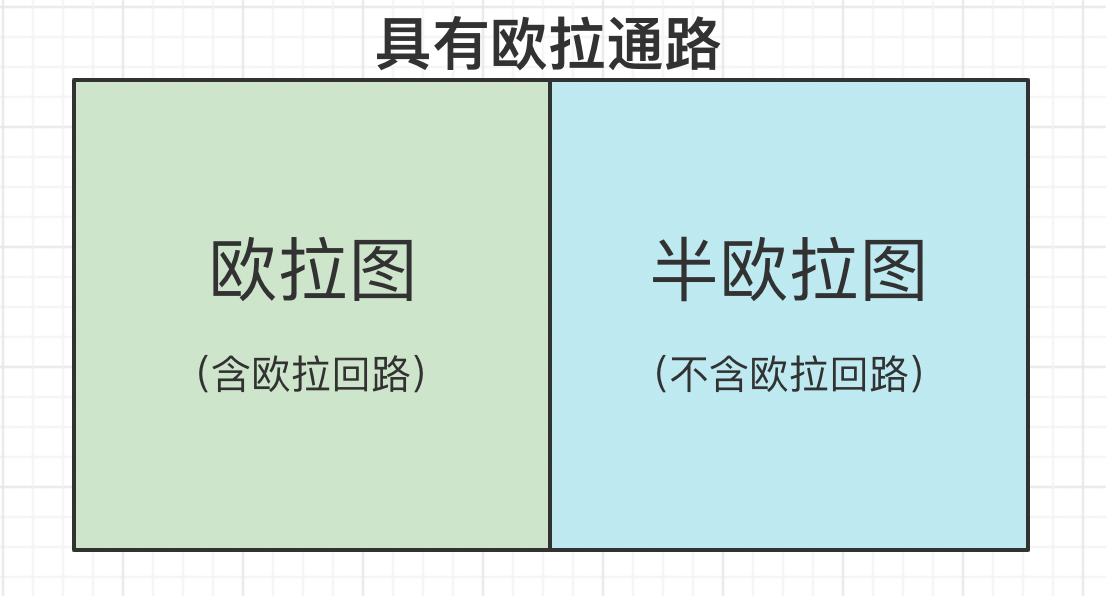
欧拉图

俗称为“一笔画”问题，关键在于不重复地遍历所有边。

具有欧拉通路而没有欧拉回路的图称作“半欧拉图”。

欧拉图的判定

对于无向图

• $无向图G是欧拉图⟺G是连通的$且不存在$度数为奇数的顶点$.
• $无向图G是半欧拉图⟺G是连通的$且恰好存在$两个度数为奇数的顶点$.
  （这两个点一个为起点，一个为终点）

对于有向图

• $有向图D是欧拉图⟺D是强连通的$且$每个顶点的出度均等于入度$.

• $有向图D是半欧拉图⟺D是单向连通的$且$恰有两个奇度顶点，其中一个顶点的入度比出度大1（终点），另一个顶点的出度比入度大1（起点），而其余顶点的入度均等于出度.$

• $G是非平凡的欧拉图⟺G是连通的$且$是若干个边不重的圈的并.$

哈密顿图

哈密顿图关键在于不重复地遍历到所有的顶点。

注意：
欧拉图要求遍历所有的边，同时也必然遍历了所有的顶点（可能会重复遍历）；
哈密顿图则是遍历所有的顶点，会有很多边不会被遍历到，而不会存在某条边被重复遍历。

哈密顿图的判定

判断一个图是否是哈密顿图是一个NP完全问题. 它是可解的。到目前为止, 还没有找到一个简明可行的条件作为一个图是否为哈密顿图的充要条件。

必要条件：

• $对于无向图G=<V,E>,V_1是V的任意非空真子集，则G是哈密顿图⟹p(G-V_1)\le |V_1|$.
  （删点后的连通分支数 ≤ 所删顶点数）

可以用这个必要条件来证明某个图不是哈密顿图。

• 有割点的图一定不是哈密顿图
• $对于无向图G=<V,E>,V_1是V的任意非空真子集,则G有哈密顿通路⟹p(G-V_1)\le |V_1|+1$.

对于二部图，设$G=<V_1,V_2,E>,|V_1|\le |V_2|,且|V_1|\ge 2,|V_2|\ge 2$，有：

• G是哈密顿图 $⟹$ $|V_2|=|V_1|$
• G中存在哈密顿通路 $⟹$ $|V_2|=|V_1|+1$
• $|V_2|\ge |V_1|+2⟹G不是哈密顿图，也不是半哈密顿图$

充分条件：

• 【狄拉克定理】$G为n(n\ge 3)阶无向简单图，\delta (D)\ge \frac{n}{2}⟹G为哈密顿图$.
• $$\begin{gathered} G为n(n\ge 3)阶无向简单图，若G中任意不相邻的顶点u、v均有d(u)+d(v)\ge n-1⟹G中存在哈密顿通路; \\ 若d(u)+d(v)\ge n⟹G为哈密顿图（存在哈密顿回路） \end{gathered}$$。【奥尔定理】

其它定理：

• $u,v为n阶无向简单图G中两个不相邻的顶点，d(u)+d(v)\ge n,则G为哈密顿图⟺G\cup (u,v)为哈密顿图$.
  （加了这样一条边后还是哈密顿图）

• $n阶竞赛图中都有哈密顿通路$。

今天的文章离散数学9：二部图、欧拉图、哈密顿图分享到此就结束了，感谢您的阅读。