线性代数投影矩阵的定义_什么是投影矩阵

About 投影矩阵

  一个矩阵$A$既可以表示一种线性变换，又可以是一个子空间（由基张开的），还可以是一组坐标，甚是神奇。

一维空间的投影矩阵

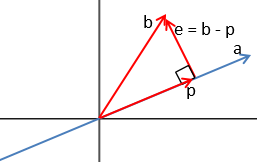
  查看上图，$p$是$b$在$a$上的投影，可以发现，$p$和$a$是同向的，故可以表示为如下形式，其中$x$是标量
$$p=ax$$
  根据$e$和$p$正交的条件，可以推导出$x=\frac{a^{T}b}{a^{T}a}$，则
$$p=a\frac{a^{T}b}{a^{T}a}=\frac{a{a}^T}{a^{T}a}b=Pb$$$$P=\frac{a{a}^T}{a^{T}a}$$
  记$P$为投影矩阵，说明了向量$b$在$a$上的投影$p$是一个矩阵作用在$b$上得到的。
$P$的性质
1.$P=P^T$，对称矩阵一定可以特征值分解
2.$rank(P)=1$，由单个向量张开的子空间，秩为1
3.$P=P^2$，投影只起一次效果

投影矩阵的多维推广

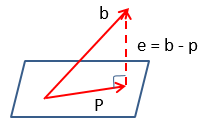
  向量$b$在子空间上的投影是向量$b$在向量$a$上投影的推广。即此时向量$a$变成矩阵$A$，记$A$的列空间包含两个向量$a_1,a_2$，依旧记向量$b$在$A$空间上的投影为$p$，则：
$$p=Ax=\left[\begin{array}{cc}{a}_1& a_2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=a_1{x}_1+a_2{x}_2$$
  误差向量$e$垂直于列空间的平面，故：
$$\{\begin{array}{r}{a}_1^T(b-p)=0\\ a_2^T(b-p)=0\end{array}$$$$A^T(b-p)=0$$$$A^T(b-Ax)=0$$$$A^{T}b=A^{T}Ax$$$$x=(A^{T}A{)}^{-1}{A}^{T}b$$
  此时投影向量$p$的形式为：
$$p=Ax=A(A^{T}A{)}^{-1}{A}^{T}b=Pb$$$$P=A(A^{T}A{)}^{-1}{A}^T$$
  这存在一个疑问，$A^{T}A$是否可逆？若$A$各列线性无关则可逆。
$P$的性质
1.$P=P^T$，对称矩阵一定可以特征值分解
2.$rank(P)=rank(A)$，由$A$张开，故等秩
3.$P=P^2$，投影只起一次效果

投影的物理意义

  向量投影到子空间的物理意义是什么？查看线性方程组$Ax=b$：
$$A=\left[\begin{array}{cccc}{a}_1& a_2& \cdots & a_n\end{array}\right],x=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$$$$b=a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n$$
  上式的物理意义：把$A$中的列向量看成$A$的列空间中的基，$x$为坐标，则向量$b$是否可用$A$中的基线性表示，若出现以下情况：向量$b$不在$A$的列空间中，则上式无解。
  此时，若将$b$投影至$A$的子空间，即$p=Pb=A(A^{T}A{)}^{-1}{A}^{T}b$，求解$A\hat{x}=p$，因为$p$最接近于$b$，所以近似解$\hat{x}$最接近于$x$，以上即为最小二乘法的几何解释，数学描述如下：
$$Ax=b$$$$A\hat{x}=A(A^{T}A{)}^{-1}{A}^{T}b$$$$\hat{x}=(A^{T}A{)}^{-1}{A}^{T}b$$

信号处理中的正交投影技术

  对于信号处理方向，矩阵论非常重要。
  假设空间由干扰源张成的子空间以及噪声子空间构成，那么如何去除干扰？
1.已知干扰
$$Q=C+P_{w}I,C=D{D}^H$$
  其中，$D$代表干扰源，$C$是由干扰源构成的协方差矩阵，$P_w$代表噪声功率。
  若干扰源已知，即$D$已知，则干扰源可用以下投影矩阵对消，全空间-干扰子空间的投影矩阵。
$$P=I-D(D^{H}D{)}^{-1}{D}^H$$$$PD=ID-DI=0$$
  综上可以发现，利用正交投影技术，可以将干扰源去掉。

2.未知干扰
  对协方差矩阵$Q$进行特征值分解，将干扰子空间和噪声子空间区分开。
$$Q=\sum _{l=1}^L{\lambda }_l{e}_l^{(i)}(e_l^{(i)}{)}^H+\sum _{l=L+1}^N{\lambda }_l{e}_l^{(n)}(e_l^{(n)}{)}^H$$$$Q=E^{(i)}{\Lambda }^{(i)}(E^{(i)}{)}^{(H)}+E^{(n)}{\Lambda }^{(n)}(E^{(n)}{)}^{(H)}$$$$Q=Q^{(i)}+Q^{(n)}$$
  因为特征向量相互正交，所以令投影矩阵$P=E^{(n)}(E^{(n)}{)}^{(H)}$，此时$PD=0$，这里的$E^{(i)}$就是由干扰$D$构成的协方差矩阵,当然，也可以写成标准形式：
$$P=I-E^{(i)}((E^{(i)}{)}^{(H)}{E}^{(i)}{)}^{-1}(E^{(i)}{)}^{(H)}$$
  因为不知道干扰，所以要对特征值及特征向量进行估计，区分哪些属于干扰子空间，哪些属于噪声子空间。

Ref：
https://www.cnblogs.com/bigmonkey/p/9897047.html

今天的文章线性代数投影矩阵的定义_什么是投影矩阵分享到此就结束了，感谢您的阅读。