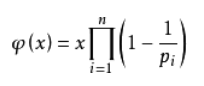数论 欧拉函数_欧拉公式常用公式

欧拉函数：

就是对于一个正整数n，小于n且和n互质的正整数（包括1）的个数，记作φ(n) 。

欧拉函数的通式：φ(n)=n*(1-1/p1)(1-1/p2)(1-1/p3)*(1-1/p4)……(1-1/pn)

其中p1, p2……pn为n的所有质因数，n是不为0的整数。φ(1)=1（唯一和1互质的数就是1本身）。

所以，根据通式我们可以打出以下代码：

ll eular(ll n)
{ 
   
    ll ans = n;
    for(int i=2; i*i <= n; ++i)
    { 
   
        if(n%i == 0)
        { 
   
            ans = ans/i*(i-1);
            while(n%i == 0)
                n/=i;
        }
    }
    if(n > 1) ans = ans/n*(n-1);
    return ans;
}

其中，if(n>1)ans-=ans/n; 这个语句是为了保证我们已经除完了n的所有的素因子，有可能还会出现一个我们未除的因子，如果结尾出现n>1 ,说明我们还剩一个素因子木有除。

打表求欧拉函数：

听说这样比较快。。。。

void euler()  
{ 
     
    for(int i=2;i<maxn;i++){ 
     
        if(!E[i])  
        for(int j=i;j<maxn;j+=i){ 
     
            if(!E[j])E[j]=j;  
            E[j]=E[j]/i*(i-1);  
        }  
    }  
}

当然，还有百度百科版的：( 欧拉筛素数同时求欧拉函数)

void get_phi()  
{ 
     
    int i, j, k;  
    k = 0;  
    for(i = 2; i < maxn; i++)  
    { 
     
        if(is_prime[i] == false)  
        { 
     
            prime[k++] = i;  
            phi[i] = i-1;  
        }  
        for(j = 0; j<k && i*prime[j]<maxn; j++)  
        { 
     
            is_prime[ i*prime[j] ] = true;  
            if(i%prime[j] == 0)  
            { 
     
                phi[ i*prime[j] ] = phi[i] * prime[j];  
                break;  
            }  
            else  
            { 
     
                phi[ i*prime[j] ] = phi[i] * (prime[j]-1);  
            }  
        }  
    }  
}  

欧拉函数的一些性质：
① 当m,n互质时，有phi（m*n）= phi（m）*phi（n）；

② 若i%p==0，有phi（i*p） = p * phi(i)；

③ 对于互质x与p，有x^phi§≡1（mod p),因此x的逆元为x^(phi§-1)，即欧拉定理。
（特别地，当p为质数时，phi（p）=p-1,此时逆元为x^(p-2)，即费马小定理）

④ 当n为奇数时，phi(2n)=phi(n)

⑤ 若x与p互质，则p-x也与p互质，因此小于p且与p互质的数之和为phi(x)*x/2;

⑥N>1，不大于N且和N互素的所有正整数的和是 1/2 *N *eular(N)。

⑦若(N%a == 0 && (N/a)%a==0) 则有:E(N)=E(N/a)*a;

⑧若(N%a==0 && (N/a)%a!=0) 则有:E(N)=E(N/a)*(a-1);

今天的文章数论 欧拉函数_欧拉公式常用公式分享到此就结束了，感谢您的阅读。