最小二乘支持向量机(LSSVM)详解
第四十六次写博客,本人数学基础不是太好,如果有幸能得到读者指正,感激不尽,希望能借此机会向大家学习。在《Feature Selection详解(附带Relief、Relief-F、LVM详解)(一)》一文中曾对支持向量机(SVM)以及支持向量回归(SVR)进行了详细的介绍,在给出二次规划问题后,需要使用SMO算法对目标进行优化,由于SMO算法运行过程中需要对原数据进行循环扫描,来查找满足条件的样本点,因此该算法的时间复杂度是非常高的,本文介绍一种解决该问题的SVM算法变体——最小二乘支持向量机(LSSVM)。
LSSVM的特性
1) 同样是对原始对偶问题进行求解,但是通过求解一个线性方程组(优化目标中的线性约束导致的)来代替SVM中的QP问题(简化求解过程),对于高维输入空间中的分类以及回归任务同样适用;
2) 实质上是求解线性矩阵方程的过程,与高斯过程(Gaussian processes),正则化网络(regularization networks)和费雪判别分析(Fisher discriminant analysis)的核版本相结合;
3) 使用了稀疏近似(用来克服使用该算法时的弊端)与稳健回归(稳健统计);
4) 使用了贝叶斯推断(Bayesian inference);
5) 可以拓展到非监督学习中:核主成分分析(kernel PCA)或密度聚类;
6) 可以拓展到递归神经网络中。
LSSVM用于分类任务
1) 优化目标
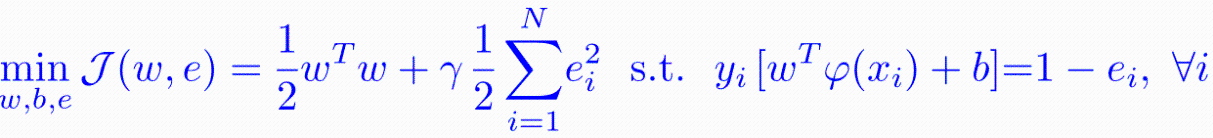
2) 拉格朗日乘子法
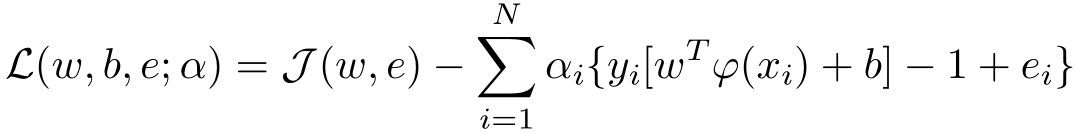
其中 α i \alpha_i αi<
今天的文章最小二乘法支持向量机原理_LS最小二乘分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:http://bianchenghao.cn/77599.html
