r语言 多因素方差分析_r语言怎么算某一行数据方差

1、当因变量（结果变量）不止一个时，可用多元方差分析（MANOVA）对它们同时进行分析。

library(MASS)
attach(UScereal)
y <- cbind(calories, fat, sugars)
aggregate(y, by = list(shelf), FUN = mean)

 Group.1 calories       fat    sugars
1       1 119.4774 0.6621338  6.295493
2       2 129.8162 1.3413488 12.507670
3       3 180.1466 1.9449071 10.856821
cov(y)

 calories       fat     sugars
calories 3895.24210 60.674383 180.380317
fat        60.67438  2.713399   3.995474
sugars    180.38032  3.995474  34.050018
fit <- manova(y ~ shelf)
summary(fit)

    Df  Pillai approx F num Df den Df  Pr(>F)   
shelf      1 0.19594    4.955      3     61 0.00383 **
Residuals 63                                          
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
summary.aov(fit)

 Response calories :
            Df Sum Sq Mean Sq F value    Pr(>F)    
shelf        1  45313   45313  13.995 0.0003983 ***
Residuals   63 203982    3238                      
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

 Response fat :
            Df  Sum Sq Mean Sq F value   Pr(>F)   
shelf        1  18.421 18.4214   7.476 0.008108 **
Residuals   63 155.236  2.4641                    
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

 Response sugars :
            Df  Sum Sq Mean Sq F value  Pr(>F)  
shelf        1  183.34  183.34   5.787 0.01909 *
Residuals   63 1995.87   31.68                  
—
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

2、评估假设检验

单因素多元方差分析有两个前提假设，一个是多元正态性，一个是方差—协方差矩阵同质性。

（1）多元正态性

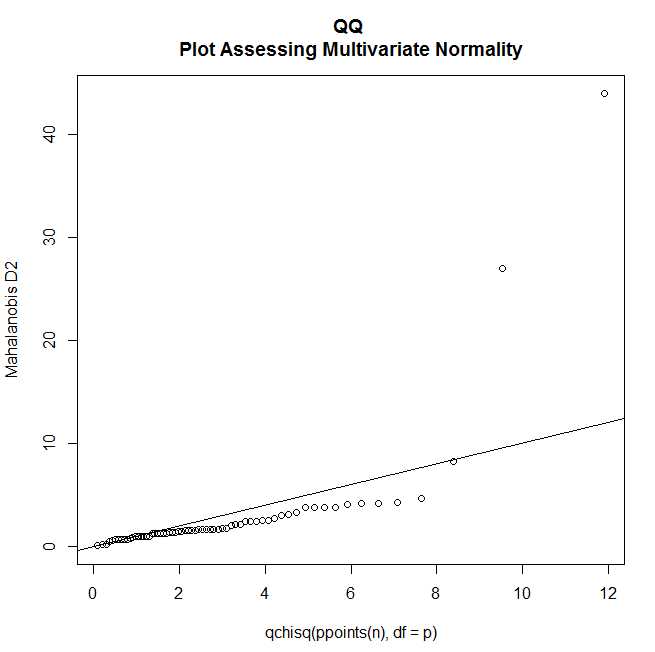
第一个假设即指因变量组合成的向量服从一个多元正态分布。可以用Q-Q图来检验该假设条件。

center <- colMeans(y)
n <- nrow(y)
p <- ncol(y)
cov <- cov(y)
d <- mahalanobis(y, center, cov)
coord <- qqplot(qchisq(ppoints(n), df = p), d, main = “QQ 
Plot Assessing Multivariate Normality”, 
    ylab = “Mahalanobis D2”)
abline(a = 0, b = 1)
identify(coord$x, coord$y, labels = row.names(UScereal))

如果所有的点都在直线上，则满足多元正太性。

2、方差—协方差矩阵同质性即指各组的协方差矩阵相同，通常可用Box’s M检验来评估该假设

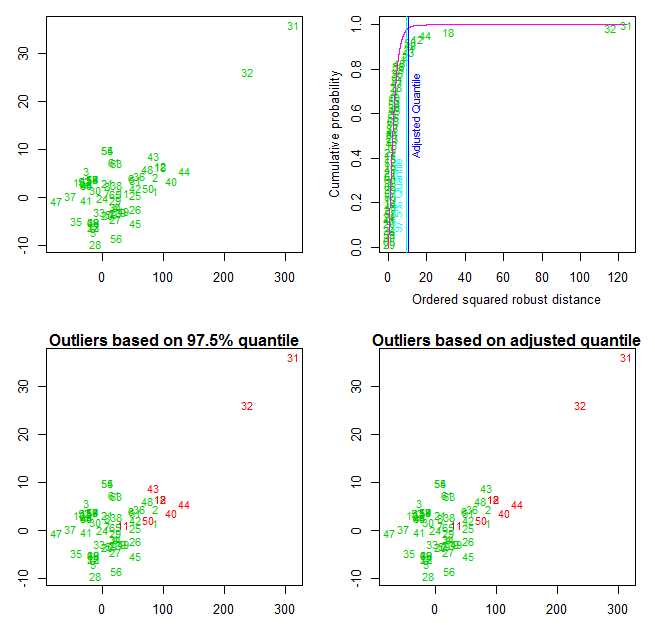
3、检测多元离群点

library(mvoutlier)
outliers <- aq.plot(y)
outliers

今天的文章r语言 多因素方差分析_r语言怎么算某一行数据方差分享到此就结束了，感谢您的阅读。