数据结构:图结构的实现方法_数据结构的实际应用举例

数据结构：图结构的实现

图(Graph)是由顶点和连接顶点的边构成的离散结构。在计算机科学中，图是最灵活的数据结构之一，很多问题都可以使用图模型进行建模求解。例如：生态环境中不同物种的相互竞争、人与人之间的社交与关系网络、化学上用图区分结构不同但分子式相同的同分异构体、分析计算机网络的拓扑结构确定两台计算机是否可以通信、找到两个城市之间的最短路径等等。

额，我都不研究这些问题。之所以重新回顾数据结构，仅仅是为了好玩。图(Graph)通常会放在树(Tree)后面介绍，树可以说只是图的特例，但是我觉得就基础算法而言，树比图复杂很多，而且听起来也没什么好玩的（左左旋、左右旋、右右旋、右左旋，好无聊～）。因此，我写的第一篇数据结构的笔记就从图开始。

1 图的概念

1.1 图的基础概念串讲

图的结构很简单，就是由顶点 $V$ 集和边 $E$ 集构成，因此图可以表示成 $G=(V,E)$ 。

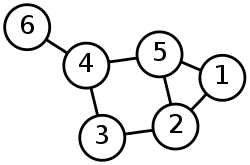
图1-1：无向图¹

图1-1就是无向图，我们可以说这张图中，有点集 V = { 1 , 2 , 3 , 4 , 5 , 6 } V=\{1, 2, 3, 4, 5, 6\} V={
1,2,3,4,5,6}，边集 E = { ( 1 , 2 ) , ( 1 , 5 ) , ( 2 , 3 ) , ( 2 , 5 ) , ( 3 , 4 ) , ( 4 , 5 ) , ( 4 , 6 ) } E=\{(1, 2), (1, 5), (2, 3), (2, 5), (3, 4), (4, 5), (4, 6)\} E={
(1,2),(1,5),(2,3),(2,5),(3,4),(4,5),(4,6)} 。在无向图中，边$(u,v)$和边$(v,u)$是一样的，因此只要记录一个就行了。简而言之，对称。

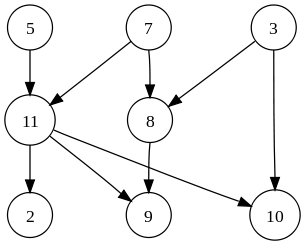
图1-2：有向图 ²
有向图也很好理解，就是加上了方向性，顶点$(u,v)$之间的关系和顶点$(v,u)$之间的关系不同，后者或许不存在。例如，地图应用中必须存储单行道的信息，避免给出错误的方向。

加权图：与加权图对应的就是无权图，如果觉得不好听，那就叫等权图。如果一张图不含权重信息，我们就认为边与边之间没有差别。不过，具体建模的时候，很多时候都需要有权重，比如对中国重要城市间道路联系的建模，总不能认为从北京去上海和从北京去广州一样远(等权)。

还有很多细化的概念，有兴趣的自己了解咯。我觉得就没必要单独拎出来写，比如：无向图中，任意两个顶点间都有边，称为无向完全图；加权图起一个新名字，叫网(network)……然而，如无必要，毋增实体。

两个重要关系：

• 邻接(adjacency)：邻接是两个顶点之间的一种关系。如果图包含$(u,v)$，则称顶点$v$与顶点$u$邻接。当然，在无向图中，这也意味着顶点$u$与顶点$v$邻接。
• 关联(incidence)：关联是边和顶点之间的关系。在有向图中，边$(u,v)$从顶点$u$开始关联到$v$，或者相反，从$v$关联到$u$。注意，有向图中，边不一定是对称的，有去无回是完全有可能的。

细化关联这个概念，就有了顶点的入度(in-degree)和出度(out-degree)。无向图中，顶点的度就是与顶点相关联的边的数目，没有入度和出度。在有向图中，我们以图1-2为例，顶点10有2个入度，$3\to 10$，$11\to 10$，但是没有从10指向其它顶点的边，因此顶点10的出度为0。

路径(path)：依次遍历顶点序列之间的边所形成的轨迹。注意，依次就意味着有序，先1后2和先2后1不一样。

简单路径：没有重复顶点的路径称为简单路径。说白了，这一趟路里没有出现绕了一圈回到同一点的情况，也就是没有环。

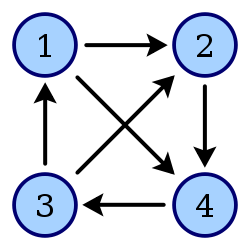
图1-3：四顶点的有向带环图³

环：包含相同的顶点两次或者两次以上。图1-3中的顶点序列$<1,2,4,3,1>$，1出现了两次，当然还有其它的环，比如$<1,4,3,1>$。

无环图：没有环的图，其中，有向无环图有特殊的名称，叫做DAG(Directed Acyline Graph)（最好记住，DAG具有一些很好性质，比如很多动态规划的问题都可以转化成DAG中的最长路径、最短路径或者路径计数的问题）。
下面这个概念很重要：

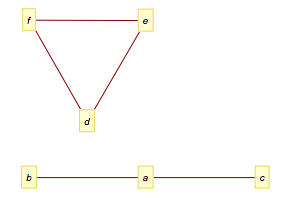
图1-4：两个连通分支

连通的：无向图中每一对不同的顶点之间都有路径。如果这个条件在有向图里也成立，那么就是强连通的。图1-4中的图不是连通的，我丝毫没有侮辱你智商的意思，我只是想和你说，这图是我画的，顶点标签有点小，应该看到a和d之间没有通路。</

今天的文章数据结构:图结构的实现方法_数据结构的实际应用举例分享到此就结束了，感谢您的阅读。