如何闭合线段_线段差的最大值的原理

求闭合区域的最外围的线段思路

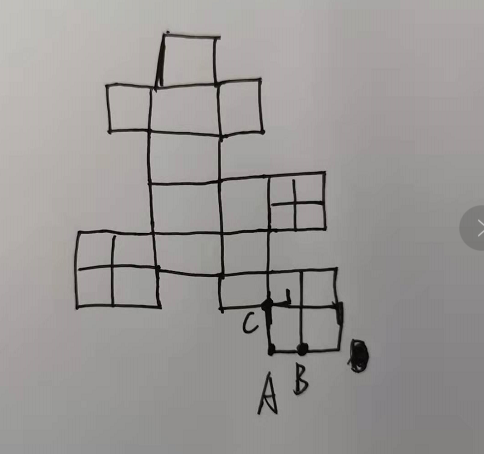
1.找起始点：获取所有的点，找到最左下点(A)点。很关键的点

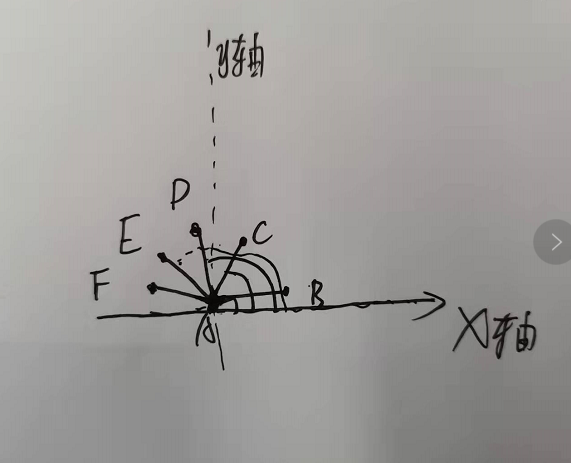
2.找起始边：首先用邻接链表存储所有点边之间的关系。找到第一条最外围的线段，根据极角来找最外围的线段，注意A是最左下角，所以上面所有连接它的线段和水平角度不会超过180度。以x轴正方向作为向量（1，0），其他向量和它做角度差，用点积求角度。可以找出AB线段。

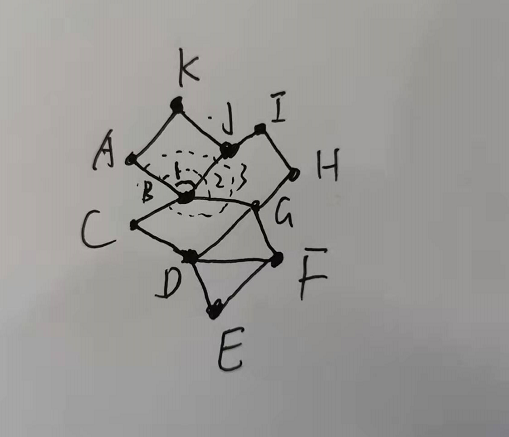
 3.找所有外边：通过角度差找最外边。如已经知道第一条外边AB边了，现在对B连接的BJ、BG、BC判断哪一条是接下来的边。通过向量叉积和点积方法，点积只能计算0到180度，无法计算超过180度，这时候利用到叉积，由于我们选的点在左下角，最后找外围线只会逆时针查找，A-B-C-D-E-F-G-H-I-J-K-A。所以0到180度的时候叉积为负，超过180度叉积为正，根据这个去计算其他边AB边的角度，角度最大就是最外边。最终会找到原点A。这样就能找到所有的最外边。

//去重
//节点去重
void CubeExportYJKHelper::GetUniquePoints(const vector<iCoord3d>& ptSets, vector<iCoord3d>& needPts)
{
	for (const iCoord3d& pt : ptSets)
	{
		bool exist = false;
		for (const iCoord3d& ic3d : needPts)
		{
			if (abs(ic3d[0] - pt[0]) < TOLERANCE && abs(ic3d[1] - pt[1]) < TOLERANCE)
			{
				exist = true;
				break;
			}
		}
		if (!exist)
			needPts.push_back(pt);
	}
}
//获取最左下角的点
void CubeExportYJKHelper::GetLeftDownPointFromPtSet(const vector<vector<pair<iCoord2d, iCoord2d>>> &areas,vector<iCoord3d> &needPts)
{
    vector<iCoord3d> points;
	//将点提取出来存储，里面会有几个重复的点
    for (const auto &var : areas)
	{
        for_each(var.begin(), var.end(), [&](const pair<iCoord2d, iCoord2d> &pt) 
		{ 
			points.emplace_back(Pt2dTo3d(YJKiCoord2d(pt.first),0));
        });
	}
    //去重
    GetUniquePoints(points, needPts);
    //对点进行排序，得到第一个最下点
    std::sort(needPts.begin(), needPts.end(), [](const iCoord3d &fpt, const iCoord3d &spt) {
		//y轴相同
        if (fpt[1] == spt[1])
            return fpt[0] < spt[0];
        else
            return fpt[1] < spt[1];
    });
}

//获取最外围的线
void CubeExportYJKHelper::GetOutsideLines(const AdjacentListGraph &graph,const int &origin,iVec2d &vec,set<int> & outsideId,
                                          pair<int, int> &lable,bool &tag)
{
    headLNode            headNode = graph.node[lable.first];
    shared_ptr<arcLNode> tempPt = headNode.firstarc;
    //记录点的位置
    int ptAdjvec;
    //判断点积
    double angle = 0;
    //线的id
    int lineId = -1;
    //获取当前点关联的所有其他点
    while (tempPt)
    {
        //如果连接起始点就结束
        if (tempPt->adjvex == lable.second)
        {
            tempPt = tempPt->nextarc;
            continue;
        }
        headLNode otherNode = graph.node[tempPt->adjvex];
        iVec2d    tempVec(otherNode.point[0] - headNode.point[0], otherNode.point[1] - headNode.point[1]);
        //先求两向量叉积，判断角度是否超过180度，由于逆时针找线，所以叉积为负，角度在0到180度，为正角度为180到360
        double crossA = vec.SignZCross(tempVec);
        
        //如果小于0
        if (crossA<=0)
        {
            //求点积
            double dotA = vec.Dot(tempVec);
            //求角度
            double mAngle = acos(dotA / (vec.Length() * tempVec.Length()))*180/PI;
            if (mAngle > angle)
            {
                angle    = mAngle;
                ptAdjvec = tempPt->adjvex; 
                lineId   = tempPt->lineId;
            }  
        }
        else
        {
            //求点积
            double dotA = vec.Dot(tempVec);
            //求角度
            double mAngle = 360 - acos(dotA / (vec.Length() * tempVec.Length())) * 180 / PI;
            if (mAngle > angle)
            {
                angle    = mAngle;
                ptAdjvec = tempPt->adjvex;
                lineId   = tempPt->lineId;
            }
        
        }
        tempPt = tempPt->nextarc;
        continue;  
    }
    //如果最终点是起始点，标记为真，结束循环，找到所有的外围线
    if (ptAdjvec == origin)
    {
        outsideId.insert(lineId);
        tag =true;
    }
    else
    {
        vec = iVec2d(headNode.point[0] - graph.node[ptAdjvec].point[0],
                     headNode.point[1] - graph.node[ptAdjvec].point[1]);
        outsideId.insert(lineId);
        lable = pair<int, int>(ptAdjvec, lable.first);
    }

}

//传入线段集合，获取最外围线段
void CubeExportYJKHelper::GetOutsideLinesFromLineSet(const vector<SegmentLine> &lines,
                                                     const vector<iCoord3d> &   points,
                                                     const iCoord3d &           startPt,
                                                     vector<SegmentLine> &      outside)
{
	//创建邻接链表
    AdjacentListGraph graph;
    graph.edgeNum = static_cast<int>(lines.size());
    graph.vertexNum = static_cast<int>(points.size());
	//存储点
    for_each(points.begin(), points.end(), [&](const iCoord3d points) {
        headLNode hNode(points);
        graph.node.emplace_back(hNode);
		});
	//存储起始点在邻接表的位置
    int originNum(0);
	//存储边的信息
    for (const SegmentLine&line:lines)
	{
		//获取边的两个端点
        vector<iCoord3d> icPt {line.startPt, line.endPt, startPt};
        vector<int>      nums;
		for (const iCoord3d&pt:icPt)
		{
            for (int i = 0; i < graph.vertexNum; ++i)
            {   
				//如果两个点的距离大于1就不是同一个点
                if (pt.DistPtPt(graph.node[i].point) > 1)
                    continue;
                nums.emplace_back(i);
                break;
            }
		}
        iCoord3d sPt(line.startPt), ePt(line.endPt);
		//获取两个点的位置
        int sNum(nums[0]), eNum(nums[1]);
        originNum = nums[2];
		//如果第一点为空
        if (!graph.node[sNum].firstarc)
        {
            std::shared_ptr<arcLNode> arcNode(new arcLNode());
            arcNode->adjvex   = eNum;
            arcNode->lineId   = line.id;
            graph.node[sNum].firstarc  = std::move(arcNode);
        }
        else
        {
            std::shared_ptr<arcLNode> tempNode = graph.node[sNum].firstarc;
			//找到最后一个节点
            while (tempNode->nextarc)
                tempNode = tempNode->nextarc;
            std::shared_ptr<arcLNode> arcNode(new arcLNode());
            arcNode->adjvex           = eNum;
            arcNode->lineId  = line.id;
            tempNode->nextarc          = std::move(arcNode);
		}
        if (!graph.node[eNum].firstarc)
        {
            std::shared_ptr<arcLNode> arcNode(new arcLNode());
            arcNode->adjvex           = sNum;
            arcNode->lineId           = line.id;
            graph.node[eNum].firstarc = std::move(arcNode);
        }
        else
        {
            std::shared_ptr<arcLNode> tempNode = graph.node[eNum].firstarc;
            //找到最后一个节点
            while (tempNode->nextarc)
                tempNode = tempNode->nextarc;
            std::shared_ptr<arcLNode> arcNode(new arcLNode());
            arcNode->adjvex  = sNum;
            arcNode->lineId  = line.id;
            tempNode->nextarc = std::move(arcNode);
        }
	}
	//最外围起始点开始查询，利用和邻边角度差求最外围线
	//找最外边，通过极角方法找最外边
    headLNode originPt = graph.node[originNum];
	//记录当前点所有关联的点形成的线段
    vector<tuple<iCoord3d, int,int>> anglePt;
    shared_ptr<arcLNode>             tempPt = originPt.firstarc; 
    //记录点的位置
    vector<int> ptAdjvec;
    //获取当前点关联的所有其他点
    while (tempPt)
    {
        anglePt.emplace_back(tuple<iCoord3d, int, int>(graph.node[tempPt->adjvex].point, tempPt->adjvex,tempPt->lineId));
        tempPt = tempPt->nextarc;
    }
    double minAngle = 360;
    int    label    = -1;
    int    lineId   = -1;
    iCoord3d point    = originPt.point;
    //最小极角就是最外边
    for_each(anglePt.begin(), anglePt.end(), [&](const tuple<iCoord3d, int,int> pt)
    { 
        iVec2d vec(get<0>(pt)[0] - point[0], get<0>(pt)[1] - point[1]);
        //向量和x轴正方向进行比较
        double angle = vec.Dot(iVec2d(1,0));
        double mAngle = acos(angle / (vec.Length() * iVec2d(1, 0).Length())) * 180 / PI;
        //如果小，记录那个点
        if (mAngle < minAngle)
        {
            minAngle = mAngle;
            label    = get<1>(pt);
            lineId   = get<2>(pt);
        }
    });
    //对起始点和起始边的另一点的访问记录
    graph.node[originNum].visited = true;
    graph.node[label].visited     = true;

    //以这条边去判断最外围的边
    bool endSearch = false;
    //c存第一条边的id
    set<int> outsideId{lineId};
    //第二个点
    iCoord3d sPt = graph.node[label].point;
    iVec2d   vec(point[0]-sPt[0],point[1]-sPt[1]);
    //存点编号，a指向b
    pair<int, int> vecLabel(label, originNum);
    //找到最外围的线，存线的id即可
    while (!endSearch) 
        GetOutsideLines(graph, originNum, vec, outsideId, vecLabel, endSearch);

    //处理最外围的线，去查找
    for (const int& var:outsideId)
    {
        for (const SegmentLine &mLine:lines)
        {
            if (var != mLine.id) continue;

            outside.emplace_back(mLine);
            break;
        }
    }
}

今天的文章如何闭合线段_线段差的最大值的原理分享到此就结束了，感谢您的阅读。