前缀 中缀 后缀表达式_前缀运算符和后缀运算符

目录

一、前缀表达式(波兰表达式)

二、中缀表达式

三、后缀表达式(逆波兰表达式)

1.逆波兰计算器

四、中缀转后缀

1.具体步骤

2.代码实现

一、前缀表达式(波兰表达式)

• 前缀表达式的运算符位于操作数之前
• 举例说明：(3+4)×5-6 所对应的前缀表达式就是 – × + 3 4 5 6 
• 从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素和次顶元素），并将结果入栈，重读上述过程直到表达式最左端，最后运算得出的值即为表达式的结果

其求值步骤如下：

1）从右至左扫描，将6、5、4、3压入堆栈

2）遇到 + 运算符，因此弹出 3 和 4 （此时3为栈顶元素，4为次顶元素），将计算出的结果 7 入栈

3）后遇到 × 运算符，因此将 7 和 5 弹出，计算出结果为 35 再次入栈

4）最后遇到 – 运算符，计算出 35 – 6 的结果 29 ，再次入栈（这时栈中只剩下一个元素，即为表达式结果） 

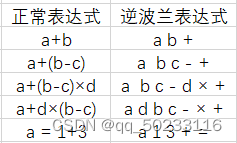
二、中缀表达式

即为常见的运算表达式，如（3+4）× 5 – 6，详细见使用栈完成表达式的计算

三、后缀表达式(逆波兰表达式)

• 与前缀表达式相似，只是运算符位于操作数之后
• 距离说明 ：(3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –

 其求值过程：

1）从左至右扫描，将 3 和 4 压入堆栈

2）遇到 + 则弹出 4 和 3 (4为栈顶元素，3为次顶元素)，计算出 3 + 4 = 7，将7压入栈中

3）将 5 入栈

4）遇到 × ，则将 5 和 7 弹出，计算出 5 × 7 = 35，再将 35 压入栈中

5）将 6 入栈

6）遇到 – ，则将 6 和 35 弹出，计算 35-6  = 29 ，将 29 压入栈中，此时这时栈中只剩下一个元素，即为表达式结果

1.逆波兰计算器

1）首先将一个逆波兰表达式依次将数据和运算符放入到ArrayList中（因为进行计算时遍历字符串效果比较低，所以换成遍历集合）

public static List<String> getListString(String suffixExpression){ //将suffixExpression分隔 String[] split = suffixExpression.split(" "); List<String> list = new ArrayList<String>(); for (String ele : split) { list.add(ele); } return list; }

2）根据逆波兰表达式的求值过程对其进行运算

public static int calculate(List<String> list){ //1.创建一个栈（只需要一个栈即可） Stack<String> stack = new Stack<String>(); //2.遍历list（因为集合没有索引值，所以使用给增强for循环来取得每一个元素）,进行运算 for (String item : list) { //2.1使用正则表达式来取出后缀表达式中的数字 if(item.matches("\\d+")) { //"\\d+":比配多位数 //2.1.1若是数字则直接入栈 stack.push(item); }else { //2.1.2若遍历时遇到运算符，则从栈中pop出两个数，并进行运算，将运算的结果再放入栈 int num1 = Integer.parseInt(stack.pop()); int num2 = Integer.parseInt(stack.pop()); int res = 0; //判断此时的运算符到底是什么运算 //此处也可以使用switch解决 if("+".equals(item)){ res = num1 + num2; }else if("-".equals(item)){ res = num2 - num1; }else if("*".equals(item)){ res = num1 * num2; }else if("/".equals(item)){ res = num2 / num1; }else { throw new RuntimeException("符号有误！"); } //2.1.3因为stack只能存String类型，而此时的res为int类型，所以需要进行转换 stack.push(res + ""); } } //3.在集合遍历完毕，且计算完毕之后栈中最后一位数即为最后的结果 return Integer.parseInt(stack.pop()); }

3）测试

public static void main(String[] args) { //定义一个逆波兰表达式 //(3+4)×5-6 --> 对应的逆波兰表达式 3 4 + 5 × 6 - String suffixExpression = "3 4 + 5 * 6 -"; int res = calculate(getListString(suffixExpression)); System.out.println(res); }

注：最后结果是小数时，则会去除小数显示整数部分，是因为将所有的计算结果转为的int型，而非double型，修改即可

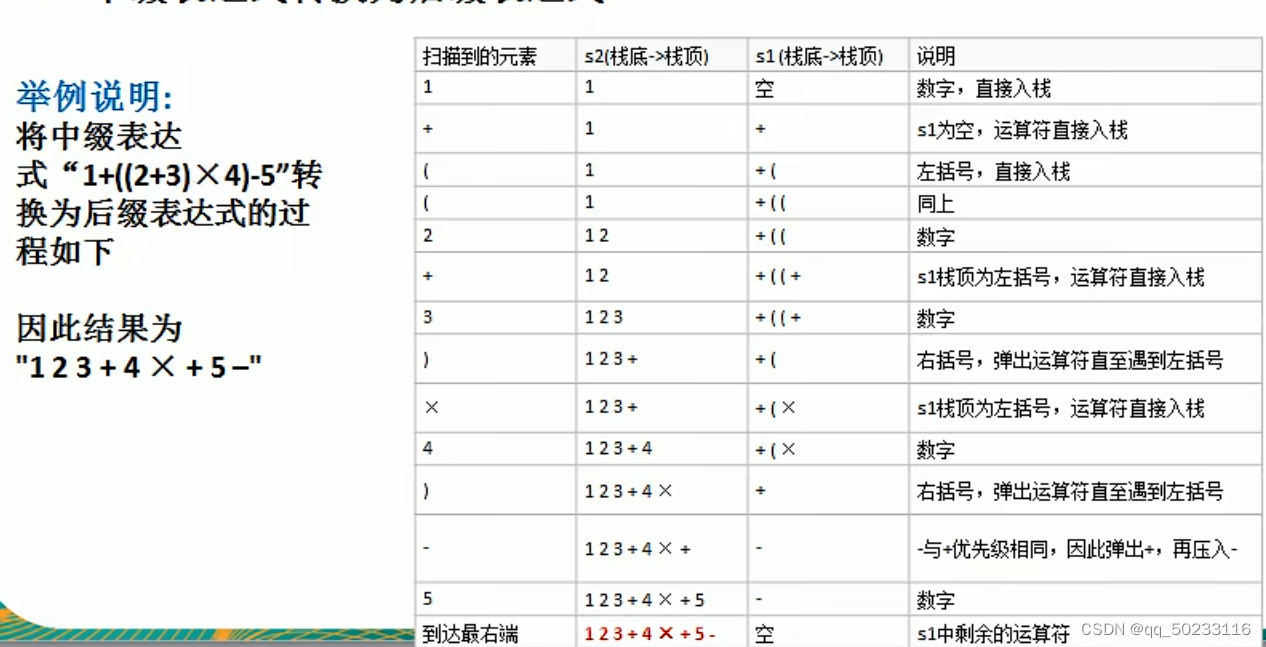
四、中缀转后缀

思路：

1.具体步骤：

        1）初始化两个栈：运算符栈s1和储存中间结果的栈s2；

        2）从左至右扫描中缀表达式

        3）遇到操作数时，将其压入栈2；

        4）遇到运算符，则比较与s1栈顶运算符的优先级

                a.如果s1为空，或栈顶运算符为左括号”(“，则直接将此运算符压入栈

                b.否则，若优先级s1比栈顶优先级高，则也直接压入栈顶

                c.若优先级s1比栈顶优先级低，则将栈顶的运算符弹出并压入s2栈中，而后再次与s1中的新栈顶进行比较

        5）遇到括号时：

                a.遇到左括号”(“时，直接压入s1栈中

                b.遇到右括号”)”时，则不断弹出s1栈顶的运算符，并压入s2中，直至遇见左括号，并将左括号也弹出（但不入任何栈，则起到了消除括号的效果）

        6)重复步骤 2 – 5 直到扫描至表达式的最右边

        7）将s1中剩余的运算符依次弹出并压入s2中

        8）依次弹出s2中的元素并输出，结果的逆序即为中缀表达式所对应的后缀表达式

2.代码实现：

1)首先，将中缀表达式转成对应的List

public static List<String> toInfixExpression(String s){ //定义一个List存放中缀表达式对应的内容 List<String> ls = new ArrayList<String>(); int i = 0; //相当于指针，用于遍历s表达式字符串 String str; //z做多位数的拼接工作 char c; //每遍历一个字符就放入c do { //如果c时非数字（运算符），就需要加入到ls中 if((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57){ //ASCII码数字范围外 ls.add(c + ""); i++; //i后移 }else { //如果时数字,需要考虑多位数的问题 str = ""; //先将str置空 while (i<s.length() && (c = s.charAt(i))<=57 && (c = s.charAt(i))>=48 ){ //判断下一个字符是否为数字 str += c; //字符串拼接 i++; //i后移继续判断 } ls.add(str); } }while (i <s .length()); return ls; }

2）创建一个类，来解决比较优先级

class Operation{ private static int ADD = 1; private static int SUB = 1; private static int MUL = 2; private static int DIV = 2; //写一个方法，返回会对应优先级数字 public static int getValue(String operation){ int res = 0; switch (operation){ case "+": res = ADD; break; case "-": res = SUB; break; case "*": res = MUL; break; case "/": res = DIV; break; default: break; } return res; } } 

3）实现中缀表达式转为后缀表达式

public static List<String> paraSuffixExpressionList(List<String> ls){ //定义两个栈 Stack<String> s1 = new Stack<String>(); //符号栈 //因为s2栈在整个转换过程中没有pop的操作，并且在最后需要一个逆序输出，所以使用ArrayList来代替使用栈 List<String> s2 = new ArrayList<String>(); for (String item : ls) { //如果是一个数，则加入到s2 if(item.matches("\\d+")){ //使用正则表达式匹配 s2.add(item); }else if("(".equals(item)){ s1.push(item); }else if(")".equals(item)){ //如果一直是”）“则依次弹出 s1 栈顶的运算符，并压入 s2 ，直到遇到左括号”（“为止 while (!"(".equals(s1.peek())){ //peek()查看栈顶元素，不弹出 s2.add(s1.pop()); } s1.pop(); //遇到左括号”（“后，将左括号”（“弹出，相当于消掉一个括号 }else { //如果不是数，是运算符 //当item的优先级小于或等于栈顶运算符，将s1栈顶的运算符弹出并加入到s2中，再次转到（4，1）与s1中新的栈顶元素安抚相比较 //缺少比较优先级高低的方法 while (s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)){ s2.add(s1.pop()); } //将item压入栈 s1.push(item); } } //将s1中剩余的运算符依次弹出并加入s2中 while (s1.size() != 0){ s2.add(s1.pop()); } return s2; //注意因为是存放到List，因此按顺序输出就是对应放入后缀表达式 }

今天的文章
前缀 中缀 后缀表达式_前缀运算符和后缀运算符分享到此就结束了，感谢您的阅读。