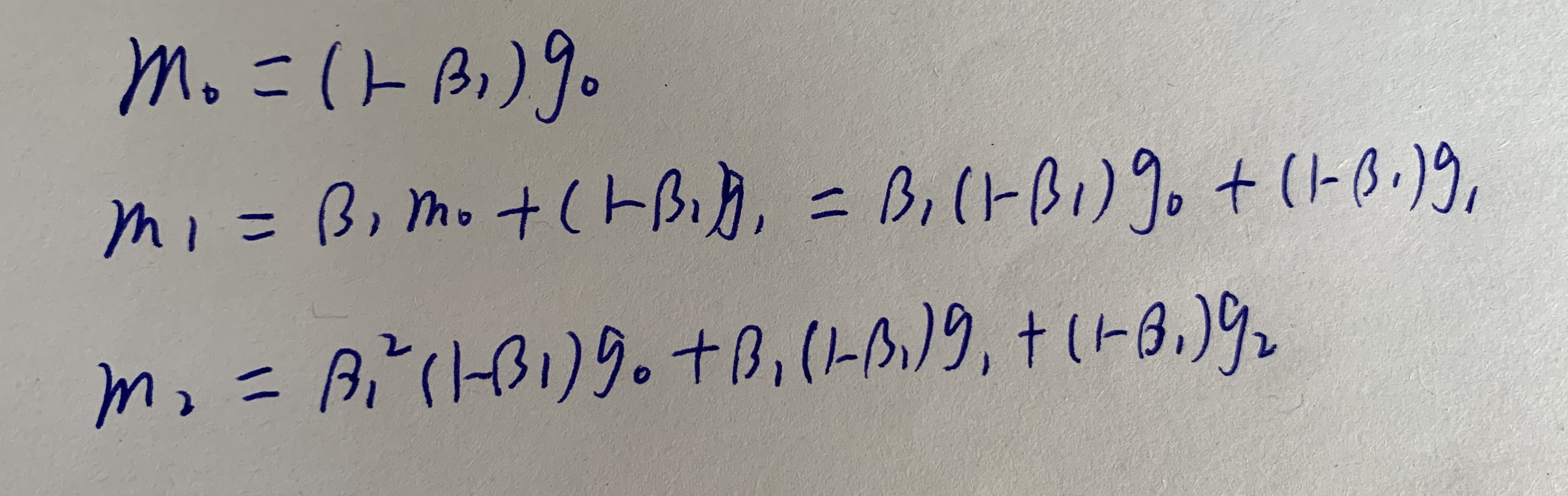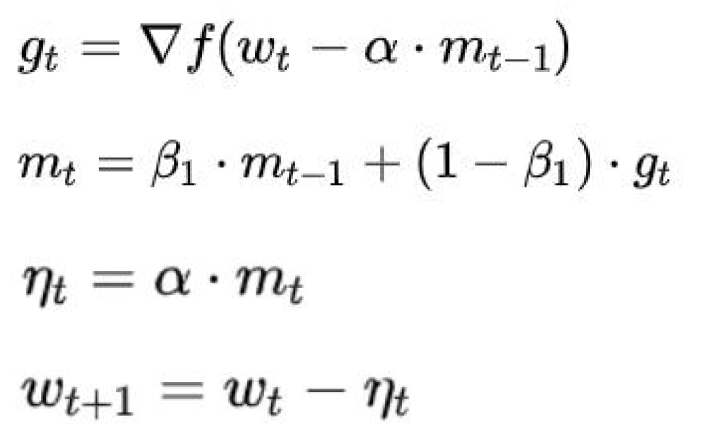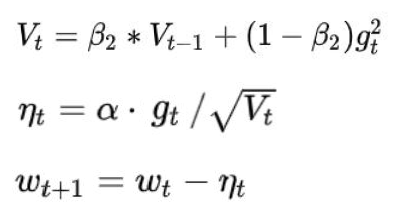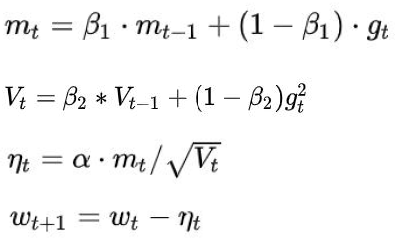深度学习训练之optimizer优化器（BGD、SGD、MBGD、SGDM、NAG、AdaGrad、AdaDelta、Adam）的最全系统详解

1、BGD（批量梯度下降）

定义：批量梯度下降法（Batch Gradient Descent，BGD）是最原始的形式，它是指在每一次
迭代时使用所有样本来进行梯度的更新。
优点：一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行。由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。
缺点：当样本数目 m 很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。

2、SGD（随机梯度下降）

定义：一次只对一个样本进行梯度下降，进行参数更新；
优点：由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快；
缺点：准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛；可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势；不易于并行实现；

2.1、SGD导致的Zigzag现象

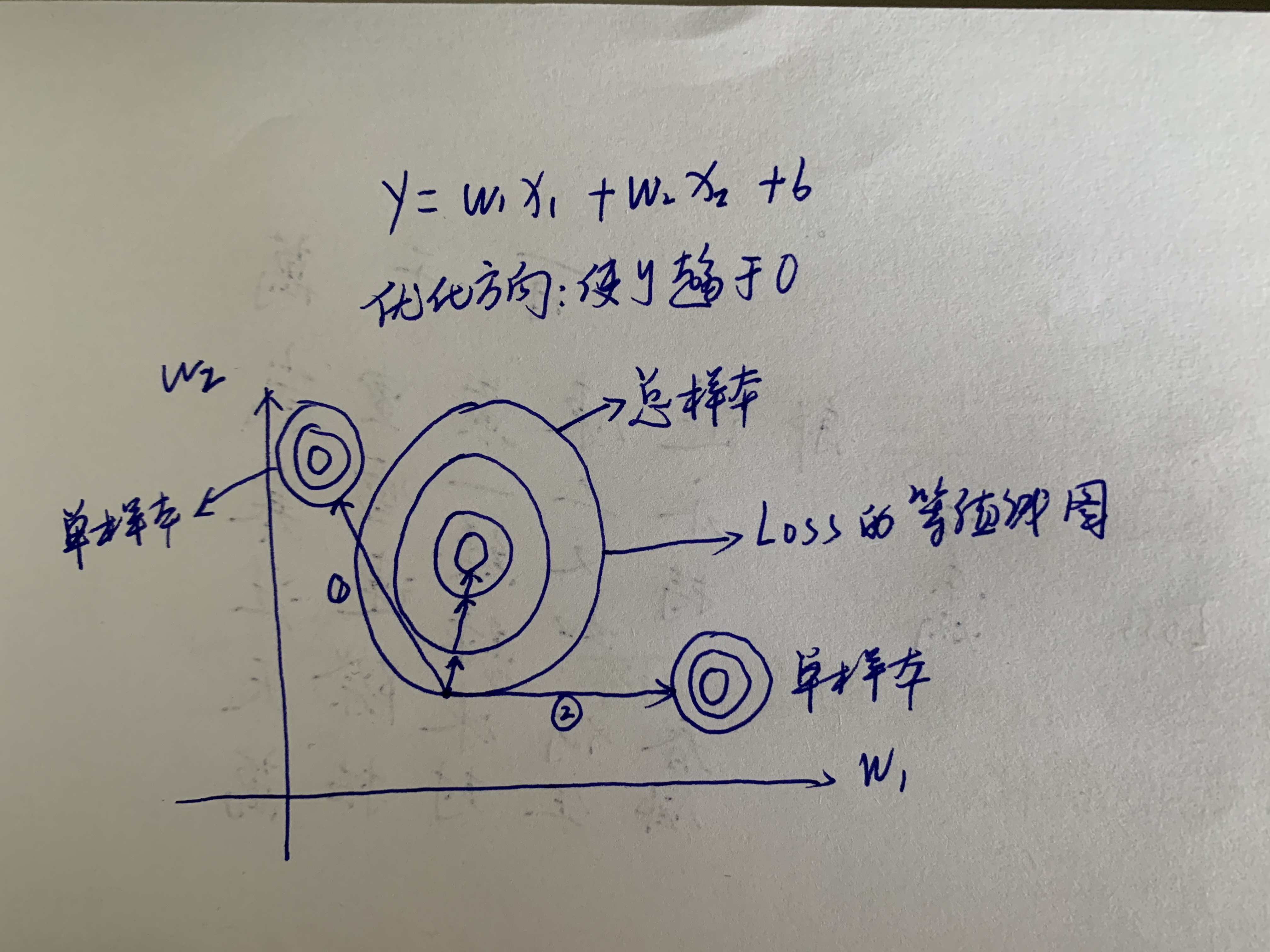
由于是随机梯度下降，下图左上角的同心圆是单样本的loss等值线图，右下角也是和左上角一样都是单样本的等值线图，可以看到如果是SGD的话，梯度下降的方向会出现不稳定，不能线性收敛，即Zigzag现象。

3、MBGD（小批量梯度下降）

定义：小批量梯度下降（Mini-Batch Gradient Descent, MBGD）是对批量梯度下降以及随
机梯度下降的一个折中办法。其思想是：每次迭代 使用指定个（batch_size）样本来对
参数进行更新。
优点：通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多。每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。
缺点：batch_size的不当选择可能会带来一些问题。

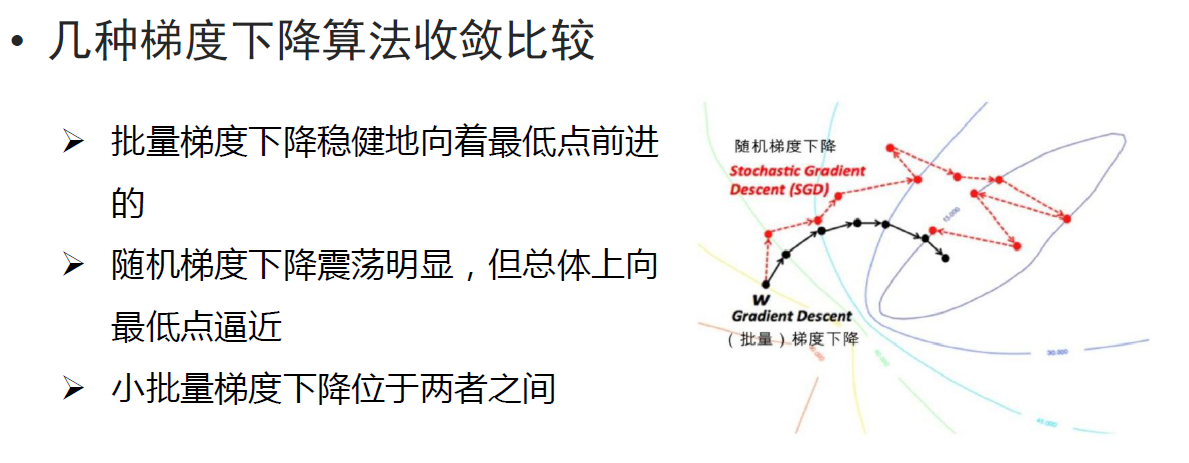
3.1 BGD、SGD、MBGD的比较

4、SGDM

全称是： Stochastic Gradient Descent with Momentum，动量随机梯度下降。

为什么提出？

因为使用SGD容易出现Zigzag现象，为了避免出现Zigzag现象，所以有了SGDM方法。

过程：
函数：$f({\omega }_t)$
${\omega }_{t+1}={\omega }_t-{\eta }_t$
${\eta }_t=\alpha \cdot m_t$，其中$\alpha$是学习率
$m_t={\beta }_1\cdot m_{t-1}+(1-{\beta }_1)\cdot g_t$
其中：
${\beta }_1$是动量参数，$m_t$是累计梯度，$g_t$是当前梯度
$g_t=\nabla f({\omega }_t)$

先对$m_t$的前三项进行展开，

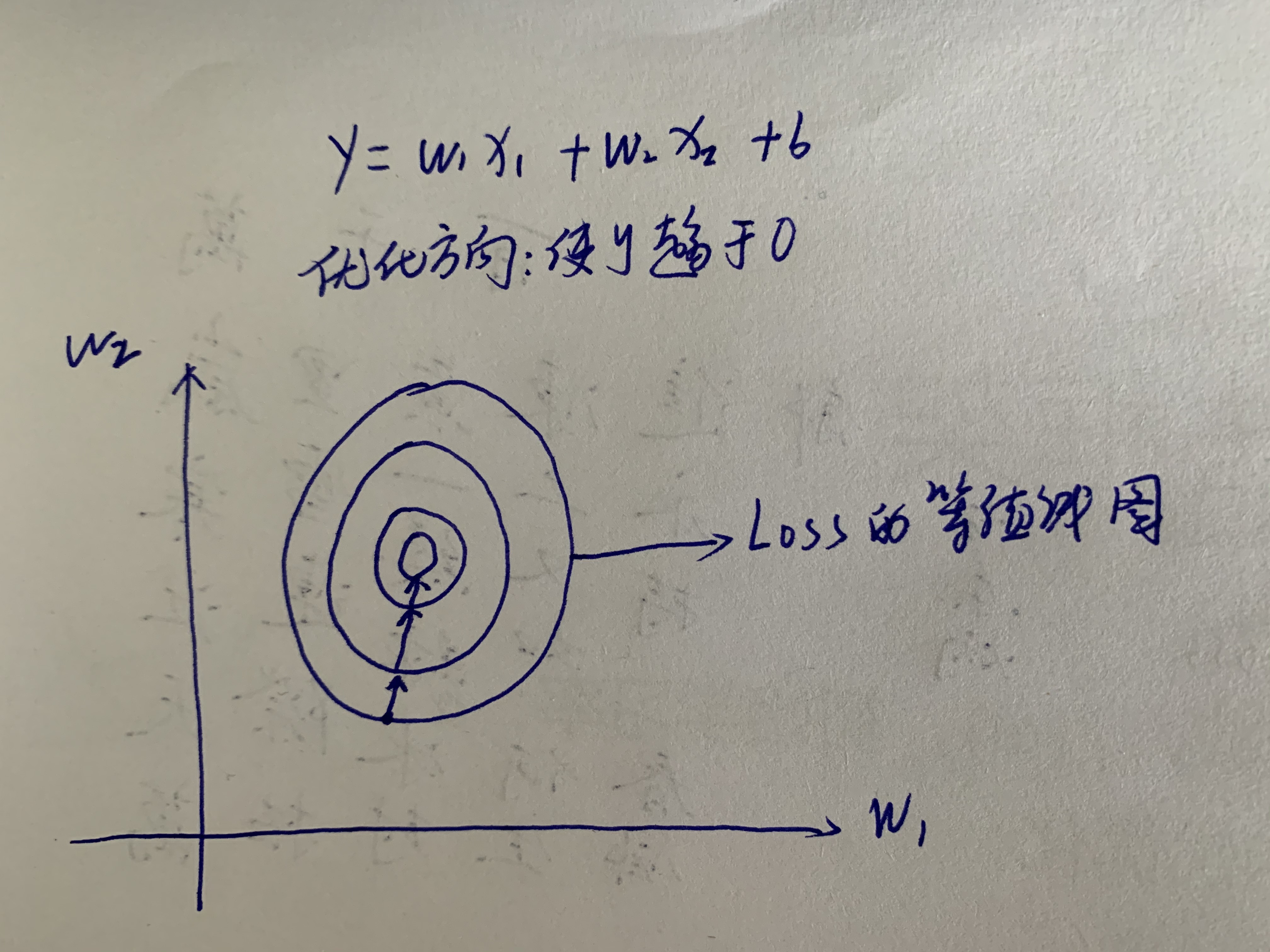
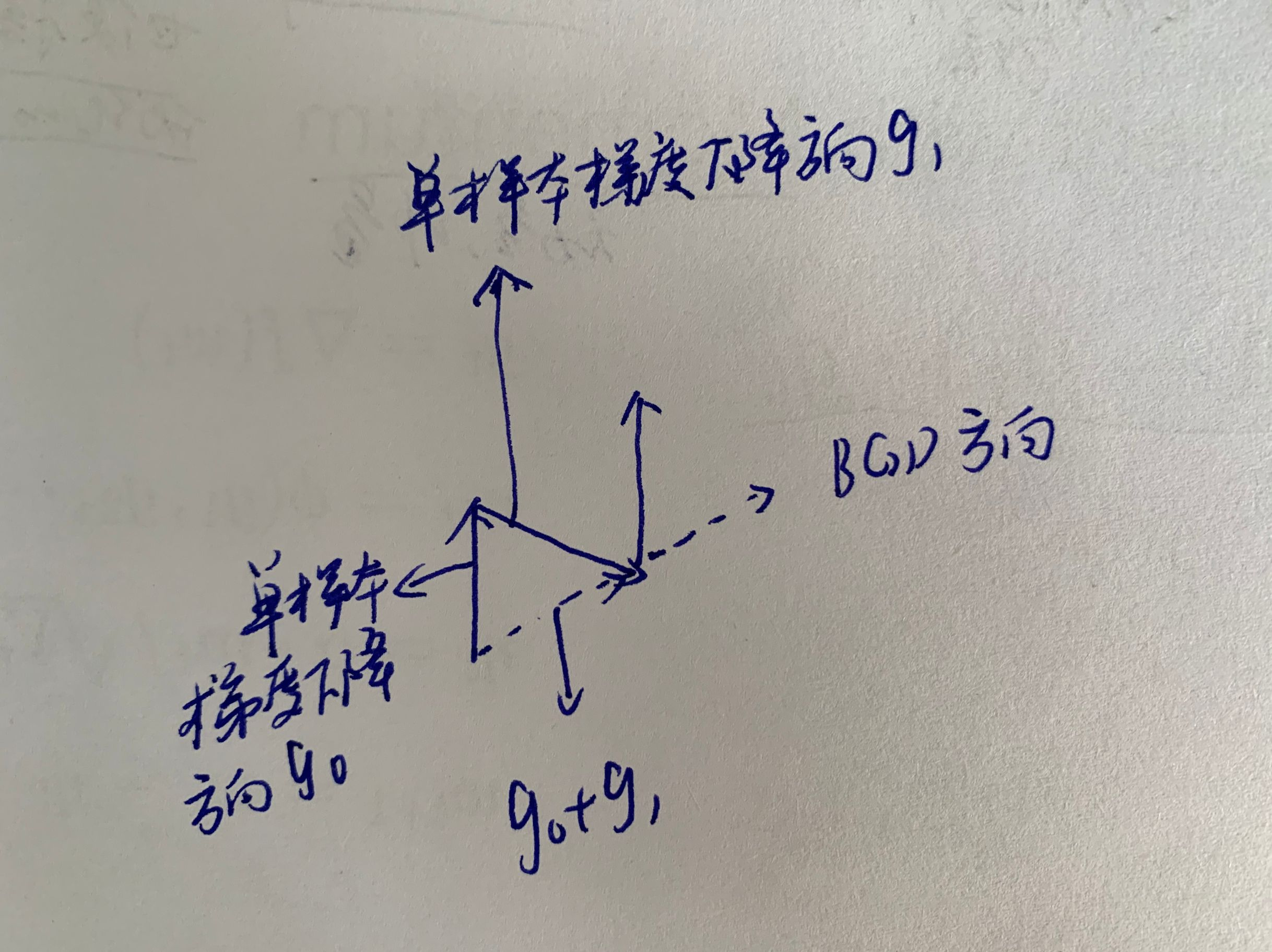
每一项的$m_t$都包含前面的所有的$g_i$，使梯度下降的方向的趋于BGD的方向，从而也趋近于我们优化的方向。
下面是关于SGDM为什么是趋近于BGD优化方向的图解，希望能看得懂，

5、NAG

全称为：Nesterov Accelerated Gradient (SGD with Nesterov Acceleration)

这个方法用的比较少，我也没有看懂，就贴一下这个方法的过程吧；

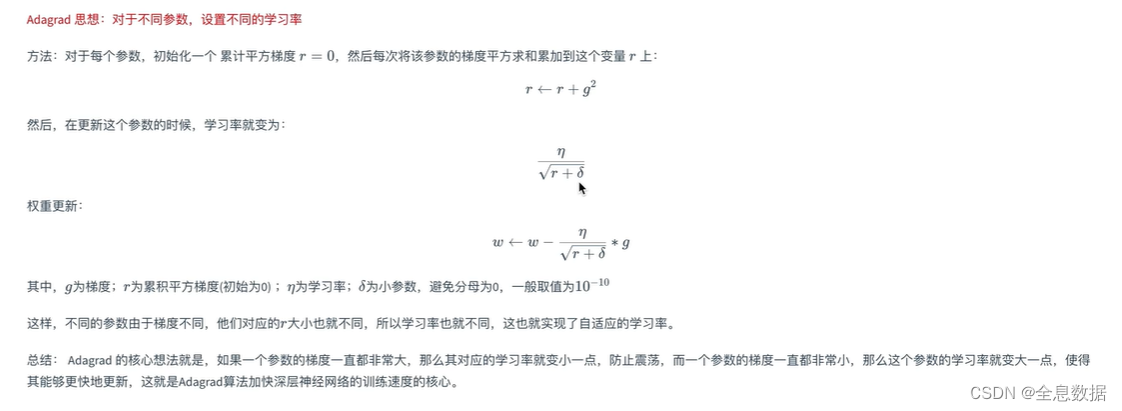
6、AdaGrad（Adaptive Gradient）

定义：自适应梯度下降，每次梯度下降时会除以前面梯度计算总和的平方再开方；每个参数都有自己独有的学习率
优点：避免前期梯度下降的梯度爆炸和弥散；
缺点：后期有可能会停止训练

$V_t={\sum }_{\tau =1}^t{g}_{\tau }^2$

${\eta }_t=\alpha \cdot g_t/\sqrt{V_t}$

${\omega }_{t+1}={\omega }_t-{\eta }_t$

7、AdaDelta/RMSProp

全称：Root Mean Square Propogation / Adaptive Delta
目的：解决AdaGrad过早收敛的问题；

8、Adam（Adaptive Moments Estimation）

结合了SGDM和AdaDelta

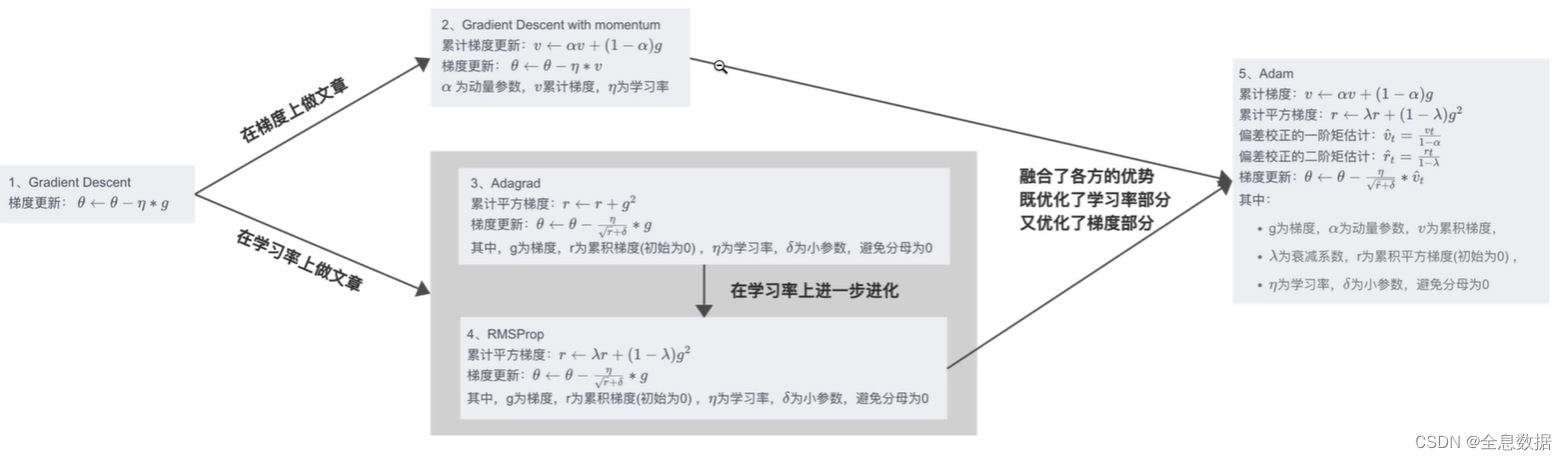
9、总结

参考：
1、哔站视频

今天的文章
深度学习训练之optimizer优化器（BGD、SGD、MBGD、SGDM、NAG、AdaGrad、AdaDelta、Adam）的最全系统详解分享到此就结束了，感谢您的阅读。