word meaning and semantic features_NLP12条预设前提详解「建议收藏」

WordNet

• WordNet是一个广泛使用的英语词汇数据库和语义网络。它由普林斯顿大学认知科学实验室开发，旨在帮助人们理解单词之间的关系和意义。WordNet的主要目标是将英语词汇组织成一种层次结构，其中每个词都与其他相关词联系起来。
• WordNet中的单词按照它们的语义关系进行分类和组织。每个单词都与一组称为”同义词集”（synset）的词组相关联。同义词集是一组具有相似含义的单词的集合，可以互相替代。WordNet中的每个同义词集都与其他同义词集通过各种关系进行连接，例如上位词（hypernyms）、下位词（hyponyms）、部分-整体关系（part-whole）、反义词等。
• WordNet在自然语言处理、信息检索、机器翻译等领域得到了广泛的应用。它提供了一个强大的资源，可以帮助计算机理解和解释单词的语义，从而改善自然语言处理应用的质量。
  

Synsets

• “synsets” 是 WordNet 中的一个重要概念，它是同义词集（synonym set）的缩写。一个同义词集是一组具有相似含义的单词的集合。在 WordNet 中，每个单词都与一个或多个同义词集相关联。
• 同义词集通过它们的语义关系将词语连接在一起。每个同义词集都包含一个核心词（称为”lemmas”），它代表了该集合的基本概念。同义词集之间的关系由 WordNet 中定义的各种关系（如上位词、下位词、部分-整体关系等）来描述。
• 通过同义词集，WordNet 提供了丰富的词汇资源，使得用户可以查找并探索单词之间的关系。例如，对于一个特定的单词，可以通过查找与之相关联的同义词集来找到其近义词、反义词、上位词等信息。同义词集的概念使得 WordNet 在词汇语义理解和自然语言处理任务中具有重要的应用价值。

Hypernymy Chain 上位词链

• Hypernymy Chain（上位词链）是在语义网络中表示词语层次结构关系的概念。在一个词汇网络中，如果一个词语可以被另一个词语的上位词（hypernym）所代表，那么它们之间存在上位关系。Hypernymy Chain 是指由一个词语经过多个层次的上位关系所形成的链条。
  例如，考虑以下词语链条的示例：
  动物 -> 哺乳动物 -> 食肉目 -> 猫科动物 -> 豹子
• 在这个示例中，每个词语都是前一个词语的上位词。动物是”哺乳动物”的上位词，”哺乳动物”是”食肉目”的上位词，依此类推。这些词语之间的层次关系可以通过Hypernymy Chain来表示。
• Hypernymy Chain 对于理解词语之间的层次关系和概念之间的继承关系非常有用。它在自然语言处理、语义理解和词义消歧等任务中被广泛应用。通过分析和利用Hypernymy Chain，可以帮助计算机系统更好地理解和组织词语的语义信息。

Hypernymy Chain 评估 Word Similarity

使用 Hypernymy Chain 衡量词语相似度的一种常见方法是通过计算词语在上位词链上的共同层级数或最短路径长度。它的发展经过了以下几个阶段：

use Path length

• 在 synsets 中的两个含义sense $c_1,c_2$
• 他们之间的路径计算公式为 $pathlen(c_1,c_2)=1+edgelength$，这里的 edge length 指的是他们之间的最短路径
• 因此他们之间的 similarity 就是距离的倒数：$$simpath(c_1,c_2)=\frac{1}{pathlen(c_1,c_2)}$$
• 两个 word 之间的相似度，就是找到他们之间最相近的含义的那个值充当。

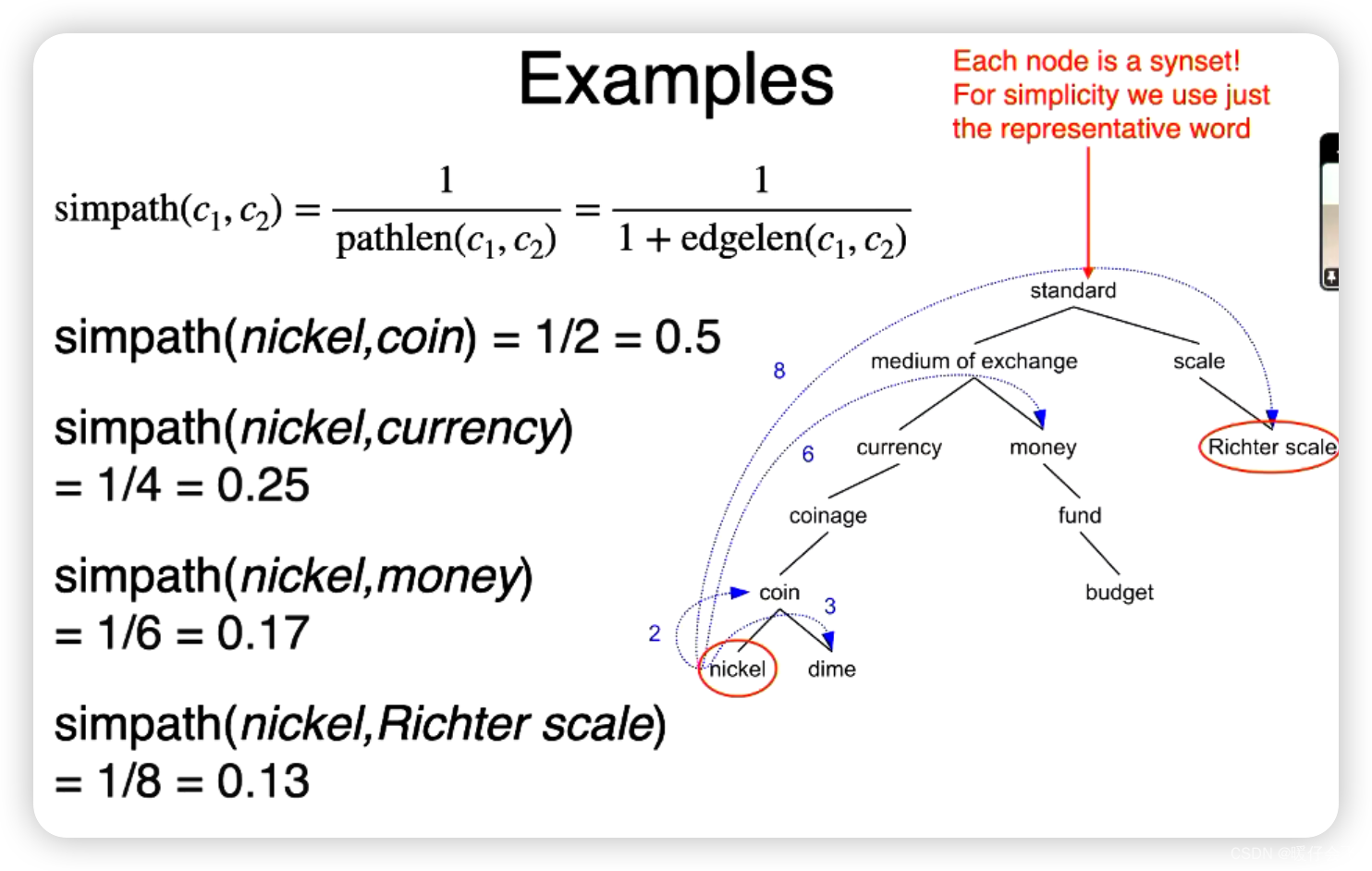
• 这个例子中， nickle 和 coin 之间的路径是 1，所以 simpath = 1/2 = 0.5
• 其他的例子也都以此类推

• 但这样存在的问题也很明显，例如 (nickle, money) 之间的 simi = 0.17 ，但是 （nickle, Richter scale) 之间的 simi=0.13
• 但其实 money 和 Richter scale 基本一点关系也没有，这就说明依靠 path 的方式存在很大的问题
• 原因是：
  • 不同的领域，其概念的层次深度可能不一样。例如，生物学的分类体系可能会比数学或物理学的更为复杂深入。这样，如果单纯以路径长度为衡量标准，可能会对不同领域的相似度评估产生偏见。
  • 路径长度并不能准确反映概念之间的相似度。例如，“狗”和“哺乳动物”之间的路径长度可能就比“狗”和“猫”之间的路径长度短，然而在实际语义相似度上，我们通常会认为“狗”与“猫”的相似度更高。
  • Hypernymy Chain 的路径长度可能会受到词汇粒度的影响。在细粒度的词汇中，可能存在更多的层级，这导致即使是非常相似的词汇，其路径长度也可能变得非常长。
  • 某些语义关系可能不会被 Hypernymy Chain 完全捕获。例如，部分横跨多个领域的概念可能会在某一领域的路径中被遗漏，这就可能导致其相似度被低估。

一种可能的解决方法就是引入深度信息

depth information

• 其中 LCS 是 $c_1,c_2$ 的最低公共祖先
• Wu & Palmer 算法的相似度计算公式为：

$$sim(c1,c2)=\frac{2\times depth(LCS(c_1,c_2))}{(depth(c_1)+depth(c_2))}$$

其中，$depth(c)$ 表示词 c 在层次结构中的深度，$depth(LCS(c_1,c_2))$ 表示 c1 和 c2 的最低公共祖先在层次结构中的深度。

• nickle, money 的深度分别是 6， 3，他们的共同最低祖先 medium of exchange 的深度为 2，因此结果是 0.44

• 但是节点的深度依然不能很好地度量语义， 接近根节点的语义应该更加抽象，而接近叶子节点的语义应该更加具象，我们需要一种方法来反映这些信息
  

• 一种很直观的想法，就是：给定一个节点，计算他所有 child 节点的 probability，这个概率和作为当前节点的概率，这样的话，一个节点的 child 越多，那么这个节点的概率值就越大。
  
  

• 从此图中就能看出来，这种方式非常好地区分了 parent 和 student 节点的概率值

• 根据这个特点，我们引入了 information content 来计算相似度

Information Content 信息量

• 公式中 $IC(LCS(c_1,c_2))$ 代表了最低的公共节点的信息量
• 信息量的计算公式 $IC=-log(P)$ 就是概率的负对数

这个算法的优点在于它同时考虑了词汇在层次结构中的深度和两个词汇之间的距离。

• 确定两个目标词语（Word A 和 Word B）以及它们在 WordNet 中的同义词集（synsets）。
• 对于每个词语的同义词集，获取其对应的 Hypernymy Chain（上位词链）。
• 比较两个词语的 Hypernymy Chain，并找到它们的最低公共上位词（Lowest Common Hypernym）或最短路径。

Word Sense Disambiguition词义消歧

今天的文章word meaning and semantic features_NLP12条预设前提详解「建议收藏」分享到此就结束了，感谢您的阅读。