一、本征半导体
纯净的具有结晶结构的半导体称为本征半导体。
1、半导体
导电特性处于导体和绝缘体之间的一类物质称为半导体。常用的半导体材料为硅(Si)和锗(Ge)。
半导体的导电特性具有热敏性和光敏性,即其在光照和热辐射的条件下,其导电性能具有明显的变化;且还具有可掺杂性,即在形成晶体结构的半导体中,人为的掺入特定的杂质元素时,导电性能可以有几百万倍的增长,从而其导电性能具有可控性。
2、本征半导体的晶体结构
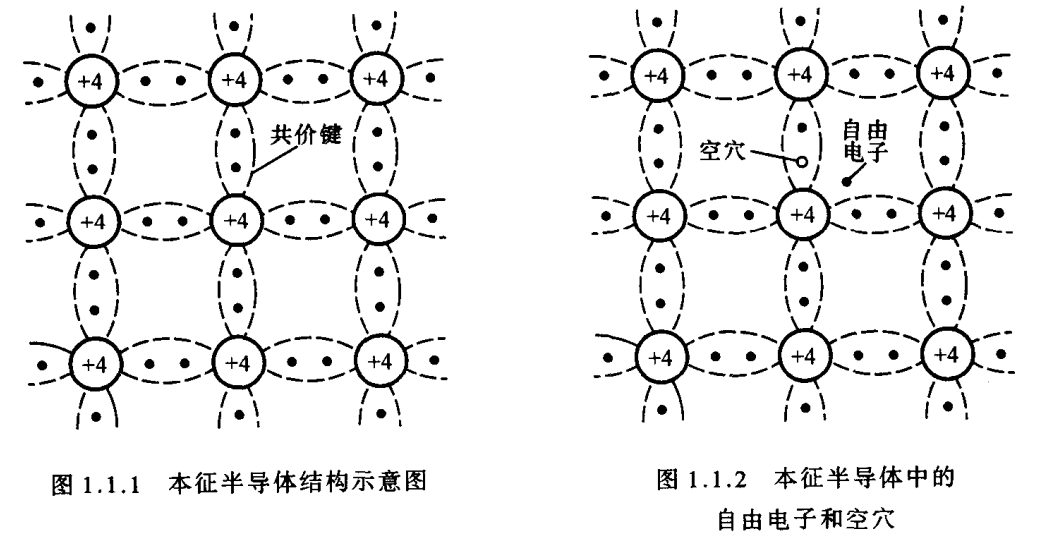
将纯净的半导体经过一定的工艺过程制成单晶体,即为本征半导体。晶体中的原子在空间形成排列整齐的点阵,称为晶格。由于相邻原子间的距离很小,因此,相邻的两个原子的一对最外层电子(即价电子)不但各自围绕自身所属的原子核运动,而且出现在相邻原子所属的轨道上,成为共用电子,这样的组合称为共价键结构,如图1.1.1所属。图中标有”+4″的圆圈表示除价电子外的正离子。
3、本征半导体中的两种载流子
晶体中的共价键具有很强的结合力,因此,在常温下,仅有极少数的价电子由于热运动(热激发)获得足够的能量,从而挣脱共价键的束缚变成为自由电子。与此同时,在共价键中留下一个空位置,称为空穴。原子因失掉一个价电子而带正电,或者说空穴带正电。在本征半导体中,自由电子与空穴是成对出现的,即自由电子与空穴数目相等,如图1.1.2所示。这样,若在本征半导体两端外加一电场,则一方面自由电子将产生定向移动,形成电子电流;另一方面由于空穴的存在,价电子将按照一定的方向依次填补空穴,也就是说空穴也产生定向移动,形成空穴电流。由于自由电子和空穴所带电荷极性不同,所以它们的运动方向相反,本征半导体的电流是两个电流之和。
运载电荷的粒子称为载流子。导体导电只有一种载流子,即自由电子导电;而本征半导体有两种载流子,即自由电子和空穴均参与导电,这是半导体导电的特殊性质。
4、本征半导体中载流子的浓度
半导体在热激发下产生自由电子和空穴对的现象称为本征激发。自由电子在运动的过程中如果与空穴相遇就会填补空穴,使两者同时消失,这种现象称为复合。在一定温度下,本征激发所产生的自由电子和空穴对,与复合的自由电子与空穴对数目相等,达到动态平衡。换言之,在一定温度下,本征半导体中载流子的浓度是一定的,并且自由电子与空穴的浓度相等。当环境温度升高时,热运动加剧,挣脱共价键束缚的自由电子增多,空穴也随之增多,即载流子的浓度升高,因而必然使得导电性能增强。反之,若环境温度降低,则载流子的浓度降低,因而导电性能变差,可见,本征半导体载流子的浓度是环境温度的函数。理论分析表明,本征半导体的载流子的浓度为
n i = p i = K 1 T 3 2 e − E G O 2 k T ( 1.1.1 ) n_i=p_i=K_1T^{\frac{3}{2}}e^{\frac{-E_{GO}}{2kT}} \kern 50pt(1.1.1) ni=pi=K1T23e2kT−EGO(1.1.1)式中 n i n_i ni 和 p i p_i pi 分别表示自由电子和空穴的浓度( c m − 3 cm^{-3} cm−3),T为热力学温度,k为玻尔兹曼常数( 8.63 ∗ 1 0 − 5 e V / K 8.63*10^{-5}eV/K 8.63∗10−5eV/K), E G O E_{GO} EGO为热力学零度时破坏共价键所需的能量,又称为禁带宽度(硅为1.21 e V eV eV,锗为0.785 e V eV eV), K 1 K_1 K1是与半导体材料载流子有效质量、有效能级密度有关的常量(硅为 3.87 ∗ 1 0 16 c m − 3 ⋅ K − 3 / 2 3.87*10^{16}cm^{-3}\cdot K^{-3/2} 3.87∗1016cm−3⋅K−3/2,锗为 1.76 ∗ 1 0 16 c m − 3 ⋅ K − 3 / 2 1.76*10^{16}cm^{-3}\cdot K^{-3/2} 1.76∗1016cm−3⋅K−3/2)。式 ( 1.1.1 ) (1.1.1) (1.1.1)表明,当 T = 0 K T=0K T=0K时,自由电子与空穴的浓度均为零,本征半导体称为绝缘体;在一定范围内,当温度升高时,本征半导体载流子的浓度近似按指数曲线升高。在常温下,即 T = 300 K T=300K T=300K时,硅材料的本征载流子浓度 n i = p i = 1.43 ∗ 1 0 10 c m − 3 n_i=p_i=1.43*10^{10}cm^{-3} ni=pi=1.43∗1010cm−3,锗材料的本征载流子浓度 n i = p i = 2.38 ∗ 1 0 13 c m − 3 n_i=p_i=2.38*10^{13}cm^{-3} ni=pi=2.38∗1013cm−3。
本征半导体的导电性能很差,且与环境温度密切相关。半导体材料性能对温度的这种敏感性,既可以用来制作热敏和光敏器件,又是造成半导体器件温度稳定性差的原因。
二、杂质半导体
通过扩散工艺,在本征半导体中掺入少量合适的杂质元素,便可得到杂质半导体。按掺入的杂质元素不同,可形成 N N N 型半导体和 P P P 型半导体;控制掺入杂质元素的浓度,就可控制杂质半导体的导电性能。
1、N型半导体
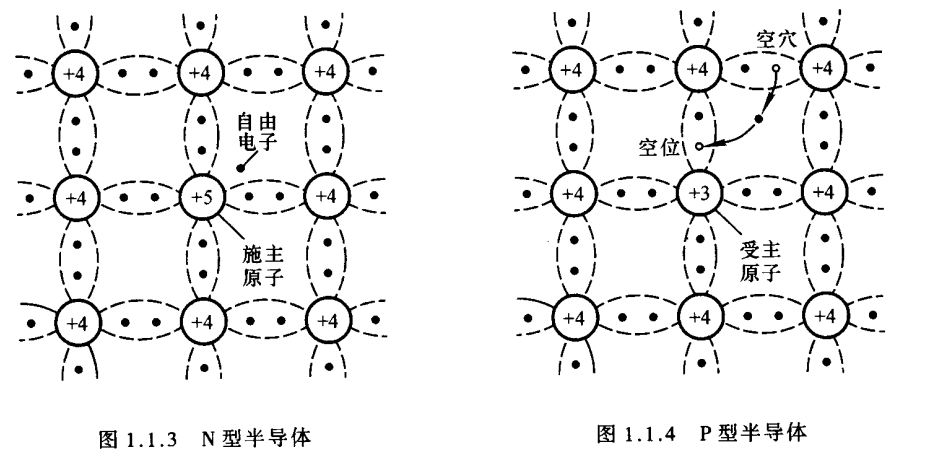
在纯净的硅晶体中掺入五价元素(如磷),使之取代晶格中硅原子的位置,就形成了 N ( N e g a t i v e ) \pmb N(Negative) N(Negative) 型半导体 。由于杂质原子的最外层有五个价电子,所以除了与其周围硅原子形成共价键外,还多出一个电子,如图1.1.3所示。多出的电子不受共价键的束缚,只需获得很少的能量,就称为自由电子。在常温下,由于热激发,就可能使它们称为自由电子。而杂质原子在晶格上,且又缺少电子,故变为不能移动的正离子。 N N N 型半导体中,自由电子的浓度大于空穴的浓度,故自由电子为多数载流子,简称多子;空穴为少数载流子,简称少子。由于杂质原子可以提供电子,故称之为施主原子。 N N N 型半导体主要靠自由电子导电,掺入的杂质越多,多子(自由电子)的浓度就越高,导电性能就越强。
2、P型半导体
在纯净的硅晶体中掺入三价元素(如硼),使之取代晶格中硅原子的位置,就形成 P ( P o s i t i v e ) \pmb P(Positive) P(Positive)型半导体。由于杂质原子的最外层有3个价电子,所以当它们与周围硅原子形成共价键时,就产生了一个“空位”(空位为电中性),当硅原子的外层电子填补此空位时,其共价键中便产生一个空穴,如同1.1.4所示,而杂质原子成为不可移动的负离子。因而 P P P 型半导体中,空穴为多子,自由电子为少子,主要靠空穴导电。与 N N N 型半导体相同,掺入的杂质越多,空穴的浓度就越高,使得导电性能越强。因杂质原子中的空位吸收电子,故称之为受主原子。
由于掺入的杂质使多子的数目大大增加,从而使多子与少子复合的机会大大增多。对于杂质半导体,多子的浓度愈高,少子的浓度就愈低。可以认为,多子的浓度约等于所掺杂原子的浓度,因而它受温度的影响很小;而少子是本征激发形成的,所以尽管其浓度很低,却对温度非常敏感,这将影响半导体器件的性能。
三、PN结
采用不同的掺杂工艺,将 P P P型半导体与 N N N 型半导体制作在同一块硅片上,在它们的交界面就形成了 P N \pmb {PN} PN结。 P N \pmb{PN} PN结具有单向导电性。
1、PN结的形成
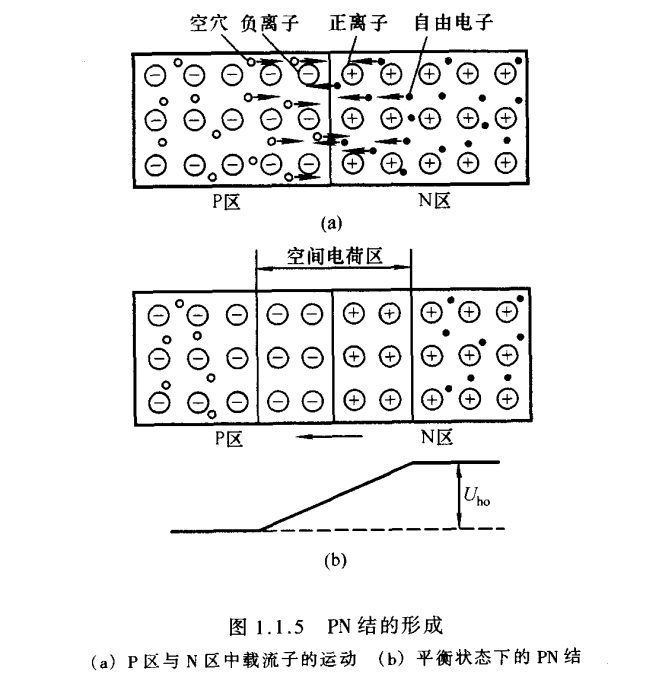
物质总是从浓度高的地方向浓度低的地方运动,这种由于浓度差而产生的运动称为扩散运动。当把 P P P 型半导体与 N N N 型半导体制作在一起时,在它们的交界面,两种载流子的浓度差很大,因而 P P P 区的空穴必然向 N N N 区扩散,与此同时, N N N区的自由电子也必然向 P P P 区扩散,如图1.1.5(a)所示。图中 P P P 区标有负号的小圆圈表示除空穴外的负离子(即受主原子), N N N 区标有正号的小圆圈表示除自由电子外的正离子(即施主原子)。由于扩散到 P P P 区的自由电子与空穴复合,而扩散到 N N N 区的空穴与自由电子复合,所以在交界面附近多子的浓度下降, P P P 区出现负离子区, N N N 区出现正离子区,它们是不能移动的,称为空间电荷区,从而形成内电场。随着扩散运动的进行,空间电荷区加宽,内电场增强,其方向由 N N N 区指向 P P P 区,正好阻止扩散运动的进行。
在电场力作用下,载流子的运动称为漂移运动。当空间电荷区形成后,在内电场作用下,少子产生漂移运动,空穴从 N N N 区向 P P P 区运动,而自由电子从 P P P 区向 N N N 区运动。在无外电场和其它激发作用下,参与扩散运动的多字数目等于参与漂移运动的少子数目,从而达到动态平衡,形成 P N PN PN结,如图1.5.1(b)所示。此时,空间电荷区具有一定的宽度,电位差为 U h o U_{ho} Uho,电流为零。空间电荷区内,正、负电荷的电量相等;因此,当 P P P 区与 N N N 区杂质浓度相等时,负离子区与正离子区的宽度也相等,称为对称结。因而当两边杂质浓度不同时,浓度高一侧的离子区宽度低于浓度低的一侧,称为不对称结;两种结的外部特性是相同的。
绝大部分空间电荷区内自由电子与空穴都非常少,在分析 P N PN PN 结特性时常忽略载流子的作用,而只考虑离子区的电荷,这种方法称为“耗尽层近似”,故也称空间电荷区为耗尽层。
2、PN结的单向导电性
(1)PN结外加正向电压时处于导通状态
当电源的正极(或正极串联电阻后)接到PN结的P端,且电源的负极(或负极串联电阻后)接到PN结的N端时,称PN结外加正向电压,也称正向接法或正向偏置。此时外电场将多数载流子推向空间电荷区,使其变窄,削弱了内电场,破坏了原来的平衡,使扩散运动加剧,漂移运动减弱。由于电源的作用,扩散运动将源源不断的进行,从而形成正向电流,PN结导通,如图1.1.6所示。PN结导通时的结压降只有零点几伏,因而应在它所在的回路中串联一个电阻,以限制回路的电流,防止PN结因正向电流过大而损坏。
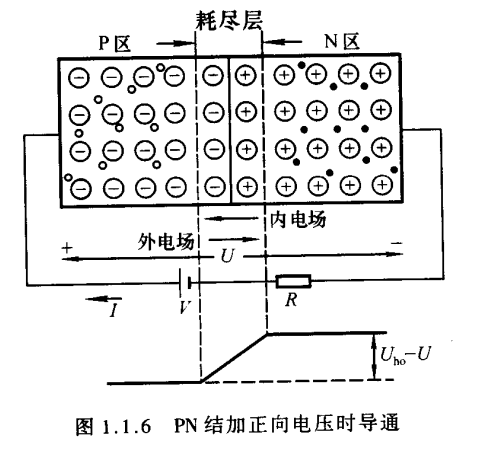
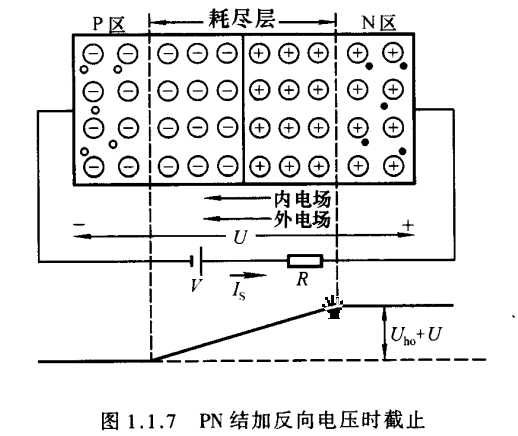
当电源的正极(或正极串联电阻后)接到PN结的N端,且电源的负极(或负极串联电阻后)接到PN结的P端,称PN结外加反向电压,也称反向接法或反向偏置,如图1.1.7所示。此时外电场使空间电荷区变宽,加强了内电场,阻止扩散运动的进行,而加剧漂移运动的进行,形成反向电流,也称漂移电流。因为少子的数目极少,即使所有的少子都参与漂移运动,反相电流也非常小,所以在近似分析中常将它忽略不计,认为PN结外加反向电压时处于截至状态。
3、PN结的电流方程
PN结所加电压 u u u 与流过它的电流 i i i 的关系为
i = I s ( e q u k T − 1 ) ( 1.1.2 ) i=I_s(e^{\frac{qu}{kT}}-1)\quad \quad \quad(1.1.2) i=Is(ekTqu−1)(1.1.2)式中 I s I_s Is为反向饱和电流, q q q 为电子的电量, k k k 为玻尔兹曼常数, T T T为热力学温度。将式(1.1.2)中的 k T / q kT/q kT/q用 U T U_{T} UT取代,则得
i = I s ( e u U T − 1 ) ( 1.1.3 ) i=I_s(e^{\frac{u}{U_T}}-1)\quad\quad\quad(1.1.3) i=Is(eUTu−1)(1.1.3)常温下,即 T = 300 K T=300K T=300K时, U T ≈ 26 m V U_T\approx26mV UT≈26mV。
4、PN结的伏安特性
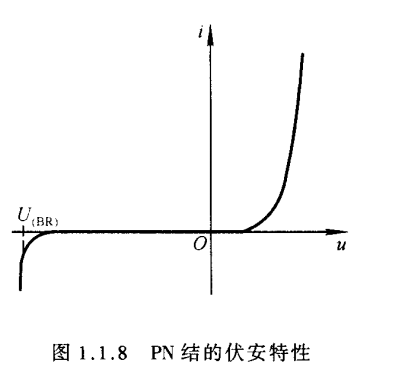
由式(1.1.3)可知,当PN结外加正向电压,且 u > > U T u>>U_T u>>UT时, i ≈ I s e u U T i\approx I_se^{\frac{u}{U_T}} i≈IseUTu,即 i i i 随 u u u 按指数规律变化;当PN结外加反向电压,且 ∣ u ∣ > > U T |u|>>U_T ∣u∣>>UT时, i ≈ − I s i\approx-I_s i≈−Is。画出 i i i 与 u u u 的关系曲线如图1.1.8所示,称为PN结的伏安特性。其中 u > 0 u>0 u>0的部分称为正向特性, u < 0 u<0 u<0的部分称为反向特性。
5、PN结的电容效应
在一定条件,PN结具有电容效应,根据产生原因不同分为势垒电容和扩散电容。
(1)势垒电容
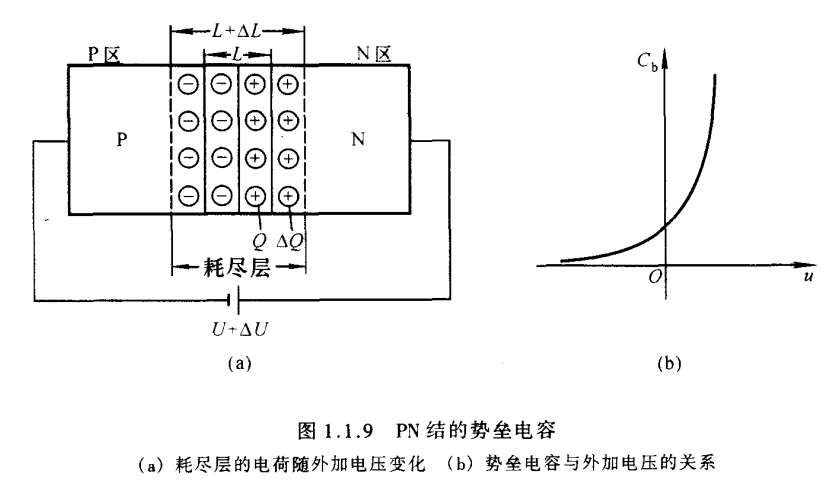
当PN结外加电压变化时,空间电荷区的宽度将随之变化,即耗尽层的电荷量随外加电压而增大或减小,这种现象与电容器的充放电过程相同,如图1.1.9(a)所示。耗尽层宽窄变化所等效的电容称为势垒电容 C b C_b Cb。 C b C_b Cb具有非线性,它与结面积、耗尽层宽度、半导体的介电常数即外加电压有关。对于一个制作好的PN结, C b C_b Cb与外加电压 u u u 的关系如图(b)所示。利用PN结加反向电压时 C b C_b Cb随 u u u 变化的特性,可制成各种变容二极管。
C b = ε S l C_b=\varepsilon \frac{S}{l} Cb=εlS
(2)扩散电容
PN结处于平衡状态时的少子常称为平衡少子。PN结处于正向偏置时,从P区扩散到N区的空穴和从N区扩散到P区的自由电子均称为非平衡少子。当外加正向电压一定时,靠近耗尽层交界面的地方非平衡少子的浓度高,而远离交界面的地方浓度低,且浓度自高到低逐渐衰减,直到零。形成一定的浓度梯度(即浓度差),从而形成扩散电流。当外加正向电压增大时,非平衡少子的浓度增大且浓度梯度也增大,从外部看正向电流(即扩散电流)增大。当外加正向电压减小时与上述变化相反。
图1.1.10所示的三条曲线是在不同正向电压下P区少子浓度的分布情况。各曲线与 n p = n p 0 n_p=n_{p0} np=np0所对应的水平线之间的面积代表了非平衡少子在扩散区域的数目。当外加电压增大时,曲线由①变为②,非平衡少子数目增多;当外加电压减小时,曲线由①变为③,非平衡少子数目减少。扩散区内,电荷的累计和释放过程与电容器充放电过程相同,这种电容效应称为扩散电容 C d C_d Cd。与 C b C_b Cb一样, C d C_d Cd也具有非线性,它与流过PN结的正向电流 i i i、温度的电压当量 U T U_T UT以及非平衡少子的寿命 τ \tau τ有关。 i i i 越大、 τ \tau τ越大、 U T U_T UT越小, C d C_d Cd就越大。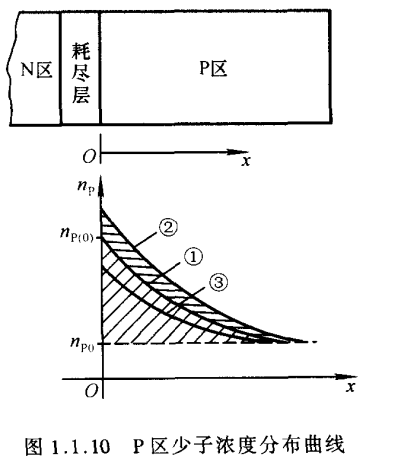
C j = C b + C d ( 1.1.4 ) C_j=C_b+C_d\quad\quad\quad\quad(1.1.4) Cj=Cb+Cd(1.1.4)
由于 C b C_b Cb与 C d C_d Cd一般都很小(结面积小的为1 pF左右,结面积大的为几十至几百皮法),对于低频信号呈现出很大的容抗,其作用可忽略不计,因而只有在信号频率较高时才考虑结电容的作用。
今天的文章
半导体基础知识整理_半导体入门知识分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/80830.html