目录
一、关联容器的概述(有序容器属于关联容器)
c++中有种关联容器,其支持通过关键字高效的查找和提取元素。而STL中定义类8种关联容器,其中每个容器都符合下列三个特点:
1、是一个map或者一个set。map保存关键字和其对应的值。而set只保存关键字。
2、要求关键字唯一(普通的map/set)或不要求唯一(带multi的set/map)
3、保持关键词有序(普通的map/set)或者不保证有序(带unordered开头的map/set)
分别为map/multimap/unordered_map/unordered_multimap,set同理的四个。
二、无序容器
该类容器其实就是使用了哈希技术来对关键字处理,以来管理元素的位置。由于里面是无序的,因此根据关键词查找单个值时非常高效,所以在处理无序的关联数据时,涉及到查找的时候,最好使用unordered_map/unordered_set。
PS:但是由于无序容器里面有个“桶”概念,因此对于multi类型的,其具有相同关键字的元素依旧是相邻存储的!
注意!
unordered_map哈希表中的键值对并不是按照插入顺序排序的,unorder_set同理。如果想直接顺序遍历键,可以借助一个数组来顺序存Key
三、有序容器
其实就是字面的意思,直接你在insert的时候,里面已经是排好序的字典了,因此如果涉及到自己定义的关键字类型,需要另外定义好元素比较的方法。
四、有序容器的最常操作—-查找方法
以一个anthors的multimap为例子,要求访问string search_item的值。
1、首先肯定是**count()+find()**的组合了—无论是关键字唯一还是关键字不唯一都适用
auto beg = anthors.find(search_item);
int num = anthors.count(search_item);
for(int i=0;i<num;++i)
{
cout << beg->second <<endl;
++beg;
}
2、使用lower_bound和upper_bound来解决。
这两个操作符都接收一个关键字,返回一个迭代器。lower_bound返回的迭代器将指向第一个具有给定关键字的元素;upper_bound返回的迭代器则指向最后一个匹配给定关键字的元素之后的位置(注意是后一个,有点前闭后开的意思)
而如果元素根本不在multimap中,lower_bound和upper_bound会返回相等的迭代器,并指向一个不影响排序的关键字插入位置——意思就是指向一个位置,这个位置就是插入该关键字的时候,应该插入的位置(有可能在某个关键字前面,有可能在尾后)
auto end = authors.upper_bound(search_item)
for(auto beg = authors.lower_bound(search_item);
beg!=end;++beg)
{
cout<< beg->second <<endl;
}
3、完全取代上面函数的equal_range函数
此函数接收一个关键字,返回一个迭代器pair。若关键字存在,则第一个迭代器指向第一个与关键字匹配的元素,第二个迭代器指向最后一个匹配元素之后的位置。而若未找到匹配元素,则两个迭代器直接指向关键字可以插入的位置。
for(auto pos = authors.equal_range(search_item);
pos.firest!=pos.second;++pos.first)
{
cout<< pos.first->second <<endl;
}
五、插入操作
普通的map可以用下标的方式,也可以完整插入。但multimap就不可以用下标了,只能是完整insert
map<int,int> a;
multimap<int,int>b;
a[0]=1;
a.insert({
0,1})
b.insert({
0,1})
六、删除操作
三种删除的方法:
1、erase(iterator it);//通过一个条目对象删除
2、erase(iterator first,iterator last);//删除一个范围
3、erase(const Key&key);//通过关键字删除
因此,在不确定有没有的时候,常常这样:
auto it = xxx.find(index);
if(it!=xxx.end()) xxx.erase(it);
七、自定义排序
需要重构运算符()。以下为例,要求将pair<int,string>排序,有限int从大到小,随后string从小到大(std的string就是字典序更小)
unordered_map<string, set<pair<int, string>, cmp>> cooks;
因此我们需要重构,如此即可。
struct cmp{
bool operator() (const pair<int, string> &a,const pair<int, string>&b)const{
return a.first==b.first?a.second<b.second : a.first>b.first;
}
};//结构体结束的分号勿忘。
若对map进行排序,则只能是对键Key进行排序,例如map<int, string, less<int>>mp。
八、有序容器的迭代器
首先,先看一下几个常见容器的迭代器类型:
| 容器 | 迭代器类型 |
|---|---|
| vector | 随机存取迭代器 |
| deque | 随机存取迭代器 |
| list | 双向迭代器 |
| multiset/set/multimap/map | 前向迭代器 |
| unorder_map/unorder_multimap/unorder_set/unorder_multiset | 双向迭代器 |
| string | 随机存取迭代器 |
其中随机存取代表着可以进行如下判断(it<it+8)[还可以用 <、>、<=、>= 运算符进行比较],而对于普通双向只可以进行it++或者it--[只能用==、!= 运算符进行比较]。前向就只能it++[只能用==、!= 运算符进行比较]。所以注意在书写判断条件时,不可以使用大于小于!下面来分别查看有序容器如何解引用呢:
【前言】首先,如何有应用有序容器存储数值时,应判断是否会有重复值,注意使用multixxx
【set的解引用】如上面的例题,我们想得到set中最开头的的string应该怎么解引用呢?
string xxx;
return (*cooks[xxx].begin()).second;
对于set,用*来解引用,通常括号内部的从右向左找,一直到*,然后解引用。如上面的就是先找到set中的开头位置,随后解引用,得到pair,然后再.second才对。因此,如果迭代器里面有嵌套成员的话,要善用()括号
【map的解引用】那如果是map,应该如何解引用呢?以 multimap<int,int>cnt = {为例:
{1,2},{3,4}};
auto it = cnt.begin();
int min_key = it->first;//取键
int min_key_value = it->second;//取值
对于set,直接用->来即可完成解引用,由于map是有序容器,因此是排好序的,在文中我们将会取值最小的key和其相应的value。
九、有序容器的应用
1、删除操作后的最大子段和(multiset+set,prev+upper_bound)
根据题目分析:
- 其实就是每次都分割,然后找到最大的子段和。因此这首先就需要用到一个有序集合来记录每个子段的和,为了能迅速地修改并且返回其最大的和,这里需要用到
multiset。即:我们每次分割完之后,我们都删掉之前字段的和,然后加入新的两个子段的和。 - 由于我们是根据删掉的下标来进行分割子段的,因此我们需要记录下标,并随时根据这些下标来找到我们分割段的范围:根据下标 p o s pos pos ,从集合中找出第一个比 p o s pos pos 大的下标 R R R,以及最后一个比 p o s pos pos 小的下标 L L L,我们将把区间 [ L + 1 , R − 1 ] [L + 1, R – 1] [L+1,R−1] 分成 [ L + 1 , p o s − 1 ] [L + 1, pos – 1] [L+1,pos−1] 以及 [ p o s + 1 , R − 1 ] [pos + 1, R – 1] [pos+1,R−1]。
这里有两个细节需要注意:
- 上面的找到第一个比pos大的下标,就需要用
upper_bound()(lower_bound()是返回大于等于);最后一个比pos小的坐标就要用prev(R);//R即区间右边界点的左边就是左边界点注意这两个函数都返回迭代器 - 上面提到了 [ L + 1 , R − 1 ] [L + 1, R – 1] [L+1,R−1],这是因为删除的点我们是不用的,因此如果找到的左右边界点都是删除元素的下标,我们需要这样取区间。由于前缀和数组的特性,因此起始边界点应为 [ 0 , n + 1 ] [0,n+1] [0,n+1]且 [ L + 1 , p o s − 1 ] [L + 1, pos – 1] [L+1,pos−1]就是前缀和数组的
pre_sum[pos-1]-pre_sum[L], [ p o s + 1 , R − 1 ] [pos + 1, R – 1] [pos+1,R−1]就是前缀和数组的pre_sum[R-1]-pre_sum[pos]。这也是前缀和数组容易错混的一个点。
class Solution {
public:
vector<long long> maximumSegmentSum(vector<int>& nums, vector<int>& removeQueries) {
vector<long long>ans;
//为例方便求区间和,这里需要用前缀和
int n = nums.size();
vector<long long>pre_sum(n+1);
for(int i=1; i<=n; i++) pre_sum[i] = pre_sum[i-1]+nums[i-1];
//记录子段长的有序集合
multiset<long long, greater<long long>>ms;
//初始情况下,整个段是一个
ms.insert(pre_sum[n]-pre_sum[0]);
//记录阻断点
set<int>st;
//初始把两端放进去,不用处理初始条件了
st.insert(0);
st.insert(n+1);
//开始处理删除操作
for(auto &pos:removeQueries)
{
pos++;//这样才对应着前缀和该数的下标
int r_p = *(st.upper_bound(pos));
int l_p = *(prev(st.upper_bound(pos)));
//删除该子段的和
ms.erase(ms.find(pre_sum[r_p-1]-pre_sum[l_p]));
//加入子段的和
if(pos-1>l_p)ms.insert(pre_sum[pos-1]-pre_sum[l_p]);
if(r_p-1>pos)ms.insert(pre_sum[r_p-1]-pre_sum[pos]);
//把间隔点放入集合中
st.insert(pos);
//每次操作,将最大值放入答案数组中
if(ms.empty()) ans.push_back(0);
else ans.push_back(*ms.begin());
}
return ans;
}
};
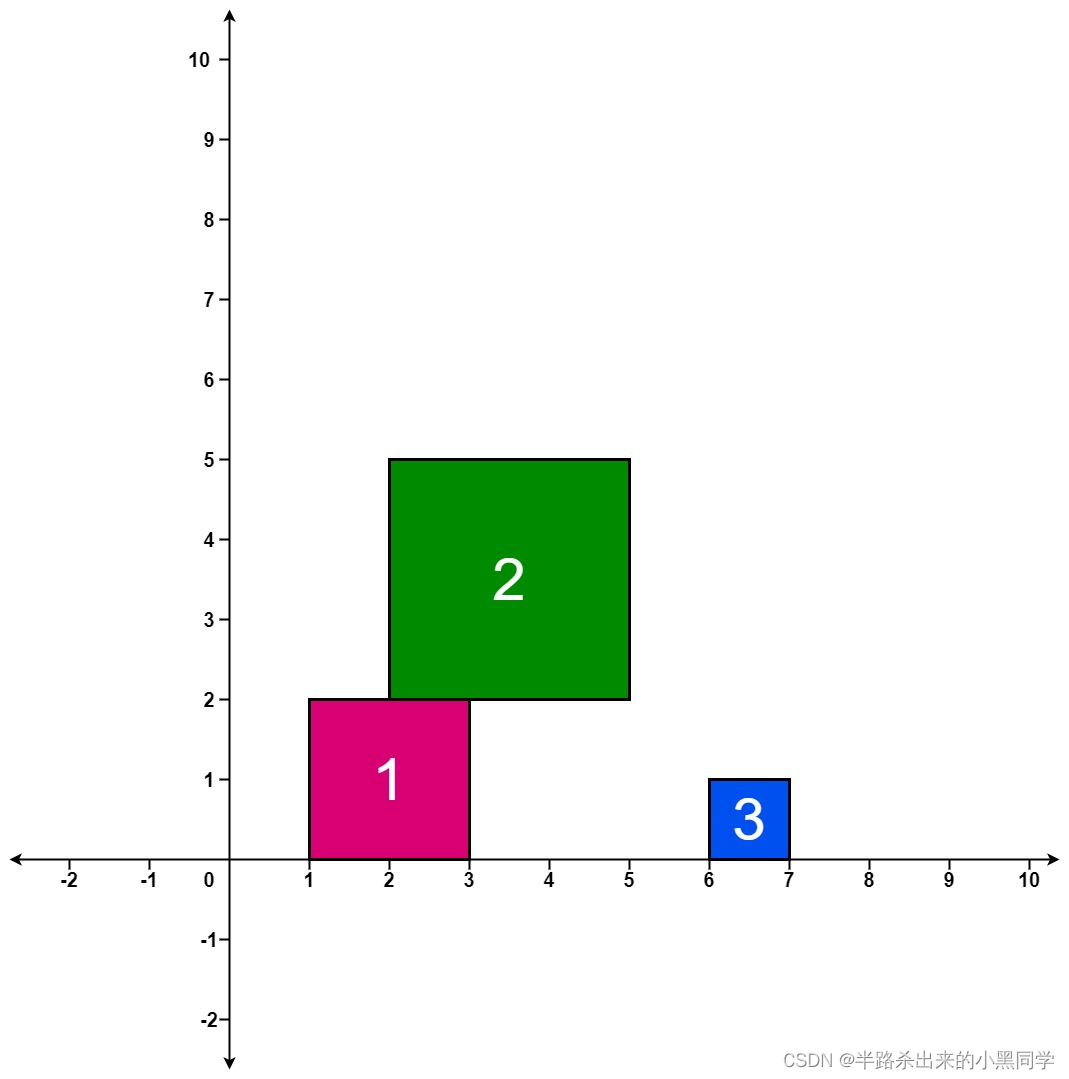
2、掉落的方块
在无限长的数轴(即 x 轴)上,我们根据给定的顺序放置对应的正方形方块。
第 i 个掉落的方块(positions[i] = (left, side_length))是正方形,其中 left 表示该方块最左边的点位置(positions[i][0]),side_length 表示该方块的边长(positions[i][1])。
每个方块的底部边缘平行于数轴(即 x 轴),并且从一个比目前所有的落地方块更高的高度掉落而下。在上一个方块结束掉落,并保持静止后,才开始掉落新方块。
方块的底边具有非常大的粘性,并将保持固定在它们所接触的任何长度表面上(无论是数轴还是其他方块)。邻接掉落的边不会过早地粘合在一起,因为只有底边才具有粘性。
返回一个堆叠高度列表 ans 。每一个堆叠高度 ans[i] 表示在通过 positions[0], positions[1], …, positions[i] 表示的方块掉落结束后,目前所有已经落稳的方块堆叠的最高高度。
暴力枚举法(迭代dp的味~)
【思想】先找到每个块放入后的所达到的高度,最后每次方块之后的最高高度!
当初这个方法都没搞定的原因是因为受困于处理一个点上的重叠问题!
而本题的标准暴力枚举,是找重叠区间的,因此就不会涉及到一个点的重叠问题,因为如果仅仅是擦边就不算重叠就ok了(本题很聪明,直接右节点减1就行了!)
其实想错了,我是创建了个新环境,从整体去记录,然而其实只根据position来找最大的高度就行了。—其实就是每新放一个块,就再模拟放一遍,从而找到最大高度
0、创建个height数组来存放每个方块落下后的高度—因为一个方块肯定整个区间都是一个值!(dp数组)
1、开始遍历position数组,遍历每一个的开始,都先把高度当作没堆叠的高度(base case)
2、新一个,都先从头再遍历一次(j<i;j++),这个遍历就检查前面所有的区间与新来的有无重叠,若有重叠就更新高度:heights[i]=max(heights[i],heights[j]+size_I )
这里才是关键,是找最大值,因为前面堆叠上的高度指不定是谁更高,也是dp思想的状态转移公式。
3、因为题目要求返回一个所有已经落稳的方块的最大堆叠高度列表,我们从 i=1 开始,加一个循环更新 h[i]=max[h[i],h[i-1]],返回h即可。此步其实旨在知道了每步的高度以后,从头开始选出每一步后最大的高度,也是一个小dp。
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
int n = positions.size();
vector<int>h(n,0);
for(int i=0;i<n;++i)
{
h[i] = positions[i][1];
int left1= positions[i][0],right1 = positions[i][0]+positions[i][1]-1;
for(int j=0 ;j<i;++j)
{
int left2 = positions[j][0],right2 = positions[j][0]+positions[j][1]-1;
if(left1<=right2 && left2<=right1) h[i]=max(h[i],h[j]+positions[i][1]);
}
}
for(int i=1 ;i<n ;++i)
{
h[i] = max(h[i],h[i-1]);
}
return h;
}
};
有序集合法—太过于技巧,不好想
其实就是优化上面的dp,上面为了检查新出现的方块与前面是否有重叠,都会重新再跑一边看看,因此能不能出个“备忘录”呢?因此就需要用到有序的映射map了。为什么有序呢,因为需要靠他来映射坐标轴从0逐渐增大。
那具体要怎么记录呢?就是用heightMap 记录每一个相对于前一个点而言,堆叠高度发生变化的点(也就是每次新方块的左右边界点)。那具体怎么实现呢,三个步骤:
1、找是否重叠,就靠指针遍历就完了—prev+upper_bound是有技巧的
2、找完重叠后,把新方块区间的所有变化点的记录都删了,因为高度统一覆盖了
3、更新新的变化的点,左节点直接更新就行,但右节点可不能随便更新。这里所说的右节点其实是right+1(因为之前为了防止同一点重叠问题最初始的right-1了),为啥不能随便更新呢,一是同一点的重叠问题;二就是由于看是否重叠是直接prev的,那么它一定指向一个东西,所以要靠right+1来阻断,让本不重叠的也拿到了重叠才有的高度。那么如何更新呢?
3.1、这里首先要明白一个事情,那就是每个新方块落下来,只更新左节点的值,然后右节点来阻断,就能形成一个表示区间的效果。因此,我只需要在新方块落下之前,记录一下原来的右边的高度多少(防止区间更新的时候被删掉),然后把原来右边赋值给新右点就可以了。这样如果重叠,新的方块左边先匹配的一定是旧左点,从而找到大高度。而若不重叠,则是旧右点,就是一个普遍的高度(此处为何叫普遍的高度呢,因为右点一开始为0,并会持续,直到有个新左点接近该右点,会把右点的值给覆盖掉,而此时旧右点的高度就也会上升了!)
3.2需要注意的是,右点不是随时都修改的,如果右点存在于哈希表中,那么就没必要赋值了,因为有可能是个更高的左值,它更能起到阻断的作用。
class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
int n = positions.size();
vector<int>ans(n,0);
map<int,int> record;
record[0]=0;//此处不如此设置,第一个就索引不到,就会爆炸
for(int i =0 ;i<n;i++)
{
int size = positions[i][1];
int left = positions[i][0],right = positions[i][0]+positions[i][1]-1;
auto lp = record.upper_bound(left),rp = record.upper_bound(right);//专门向后找,然后prev操作
//若右边没有值,那么需要确定右边的阻断点,该点的值就是普遍的高度(即不堆叠,放下应该是多高)
int rp_1 = prev(rp)->second;//prev()是双向迭代器的反向前进
int height = 0;
//1是否重叠的判断
for(auto p = prev(lp);p!=rp;++p)
{
height = max(height,p->second+size);
}
//2判断完后,把区间内的记录清除,因为都依靠左边节点的高度来显示整个区间
record.erase(lp,rp);
//3左点一定要更新(它代表着这个区间的高度),右点看是否存在再更新(仅仅为了阻断而已)
record[left] = height;
// 此处的判断是通用的,详细可看四中的2,不存在时是两种情况,尾或者插入位置,rp由于是upper所以应该指向后一个
if(rp==record.end()||rp->first != right + 1)record[right+1] = rp_1;
int tem = i>0?max(height,ans[i-1]):height;
ans[i] = tem;
}
return ans;
}
};
总结此类:
1、哈希表模拟一个区间,完全可以仅用左点来表示重叠后的基准高度,右点来当作不重叠的基准高度。(故一开始要放个【0】=0,作为不重叠基准)
然后通过upper_bound+prev来找重叠不重叠。
2、哈希表可以用erase来快速清理一个区间的数值
3、用upper_bound判断元素在不在是需要两个条件的,左点更新直接更即可,但右点的更新为了防止erase清除以前的基准高度,需要提前先记录下来右点的高度,后赋值。
下面附上力扣官方题解(以后大概率不会化那么久搞了!真的不知所云啊,我这个菜鸟花了大概两个小时才完全搞明白!)
对于第 ii 个掉落的方块,记它底部的左端点为left,右端点为 right。我们在有序集合中查找该区间[left,right] 内所有点的堆叠高度,然后更新该方块对应的堆叠高度 height。在第 ii 个方块掉落后,区间[left,right] 内的所有点的堆叠高度都是 height,因此我们将有序集合里对应区间 [left,right] 内的点全部删除。该掉落的方块带来的堆叠高度变化主要在两个点,即 left 和 right+1,更新对应的变化即可。
今天的文章c++有序表_用户界面中的容器包括分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/81669.html