线性规划基可行解怎么求_怎么确定基可行解

昨天查了不能说一晚上吧，也差不多，不知道是问题太简单了还是没有多少能说清楚的，但至少网上的回答令我大失所望，让我云里雾里的，完全迷惑了这些名词到底是个啥，如何清楚的理解它们。

幸好之前搞了一本清华大学出版社出版的《运筹学基础》，晚上泡脚的时候终于搞明白了这些概念。为让跟我一样困惑的初学者们能清楚的理解它们的含义，故此记录。

首先我们先列出线性规划的数学模型，通过该模型来一一说明每个概念的含义。


$$maxZ=\mathbf{c}\mathbf{x}\text{\hspace{1em}(1)}$$
$$s.t.\mathbf{A}\mathbf{x}=\mathbf{b}\text{\hspace{1em}(2)}$$
$$\mathbf{x}\ge 0\text{\hspace{1em}(3)}$$ 其中，
$\mathbf{A}$是
$m\ast n$ 的矩阵（系数矩阵），
$r(A)=m$表示线性规划模型的秩，且
$n>m$。


注：这说明方程个数=r

可行解

凡是满足约束条件（2）和（3）的解 $\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$称为线性规划问题的可行解，同时满足目标函数（1）的可行解成为最优解。

基向量和非基向量

设线性规划约束方程组中的系数矩阵$\mathbf{A}$的秩为$m(n>m)$,则$\mathbf{A}$中任一个$\mathbf{m}$阶可逆矩阵$\mathbf{B}$ 称为线性规划问题的一个基矩阵，简称基。记 $\mathbf{B}=({\mathbf{p}}_1,{\mathbf{p}}_2,\cdots ,{\mathbf{p}}_{\mathbf{m}})$，则称$p_j(j=1,2,\cdots ,m)$ 为$\mathbf{B}$的一个基向量，而$\mathbf{A}$ 中剩余$n-m$个列向量称为非基向量。

何为任一？
也就是说 $\mathbf{B}$ 是矩阵 $\mathbf{A}$ 中任一m列组成的矩阵，那么$\mathbf{B}$ 可以表示为（假设矩阵$\mathbf{A}$有四列，$r=2$）：
$\mathbf{B}=({\mathbf{p}}_1,{\mathbf{p}}_2)\mathbf{o}\mathbf{r}\mathbf{B}=({\mathbf{p}}_1,{\mathbf{p}}_3)\mathbf{o}\mathbf{r}\mathbf{B}=({\mathbf{p}}_1,{\mathbf{p}}_4)\mathbf{o}\mathbf{r}\mathbf{B}=({\mathbf{p}}_2,{\mathbf{p}}_3)\mathbf{o}\mathbf{r}\mathbf{B}=({\mathbf{p}}_2,{\mathbf{p}}_4)\mathbf{o}\mathbf{r}\mathbf{B}=({\mathbf{p}}_3,{\mathbf{p}}_4)$ , 只要$\mathbf{B}$可逆，即$|\mathbf{B}|\ne 0$, 则就有基本解，也就是后边提到的线性规划最多有基本解的个数为 $C{}_n^m$

基变量、非基变量、基解

取$\mathbf{A}$中一个基$\mathbf{B}=({\mathbf{p}}_1,{\mathbf{p}}_2,\cdots ,{\mathbf{p}}_{\mathbf{m}})$ , 对应的基变量为${\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_{\mathbf{m}}$, 则${\mathbf{x}}_{\mathbf{m}+1},{\mathbf{x}}_{\mathbf{m}+2},\cdots ,{\mathbf{x}}_{\mathbf{n}}$ 为非基变量，当非基变量取值均为零时且满足约束（2）的一个解$x$ 称为关于基$\mathbf{B}$的一个基本解，线性规划问题最多只有$C{}_n^m$个基本解

基本可行解

若一个基本解$x$同时满足非负约束条件（3），则称$x$为基本可行解。

图解

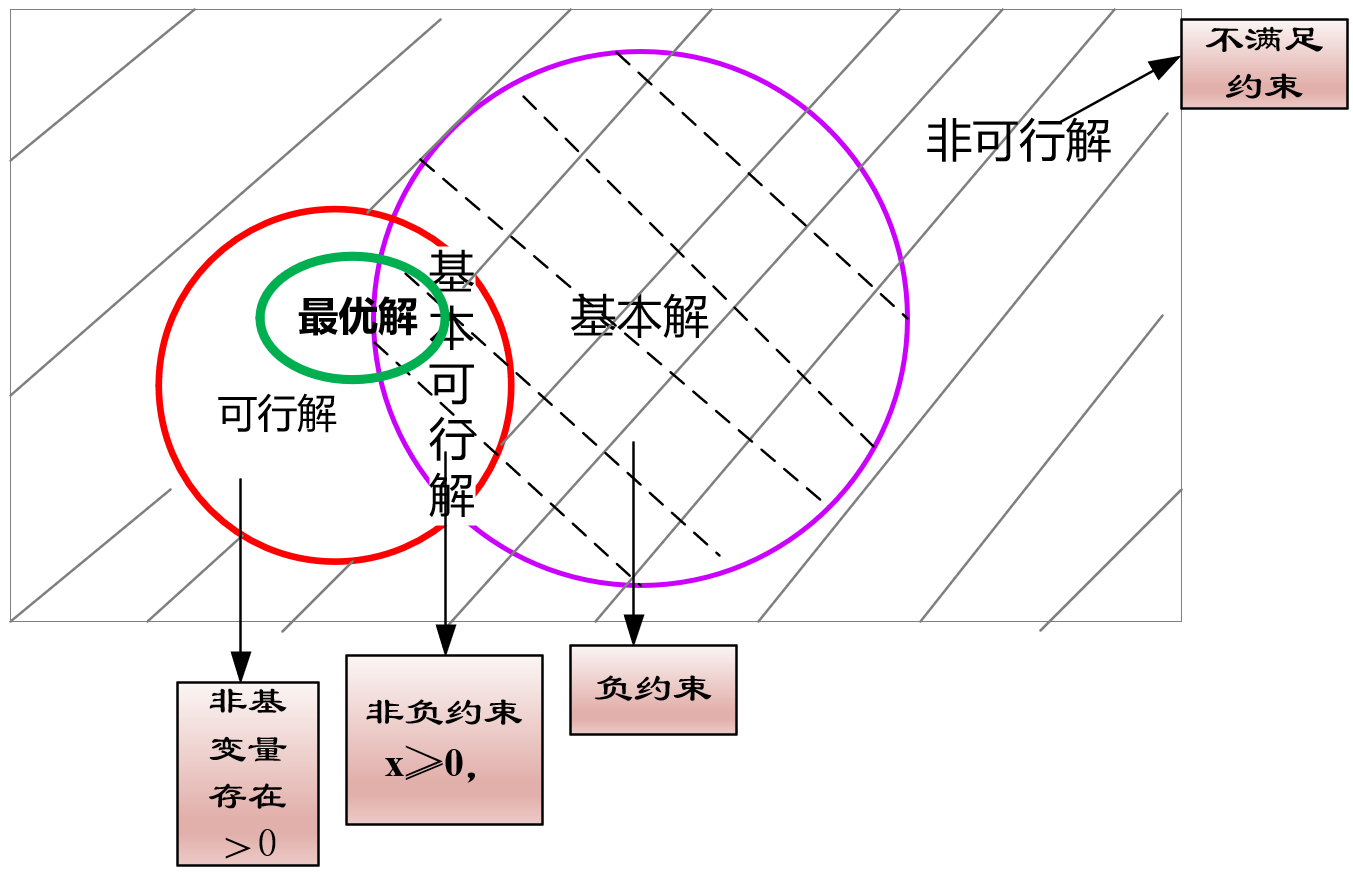
其实，这些概念的大小关系可以通过一张图完美的解释，上图

从图中我们可以得出这样的一些结论（自己理解）：

1. 可行解或者基本解是针对约束而言的，最优解是针对约束和目标函数而言的；
2. 基本可行解是可行解的一个特解；
3. 基本解中存在非可行性解，换句话说非可行解最多只满足约束中的一个，而不能同时满足两个约束，也存在非可行解满足目标函数，但不完全满足约束的情况

第三条或许就是为什么很多多目标EA对比分析feasible solutions 和infeasible solutions的原因了。但在例如NSGA中 infeasible solution与feasible solution是在constraint中提到的，感觉是为了保证多样性，即使两个均为infeasible solution，还是选择了smaller constraint violation的那个解，让其拥有better Pareto Rank。

疑问：是不是所谓的最优解中存在infeasible solutions呢？（🐶）

今天的文章线性规划基可行解怎么求_怎么确定基可行解分享到此就结束了，感谢您的阅读。