点乘积和叉乘积的区别_向量积与数量积的区别

序言

• 区分一下这几个概念

1. 点乘

• 点乘 = 点积 = 内积 = 数量积
• dot product = inner product = scalar product
• $\vec{a}=(x_1,y_1,z_1)$，$\vec{b}=(x_2,y_2,z_2)$
• 从代数角度看，点积是对两个向量对应位置上的值相乘再相加的操作，其结果即为点积

$$\vec{a}\bullet \vec{b}=x_1{x}_2+y_1{y}_2+z_1{z}_2$$

• 点乘的几何意义：向量b在向量a方向上的投影与向量a的模的乘积，用来表征或计算两个向量间的夹角，表征两个向量在方向上的相似度，结果越大越相似

$$\vec{a}\bullet \vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\cos \theta$$

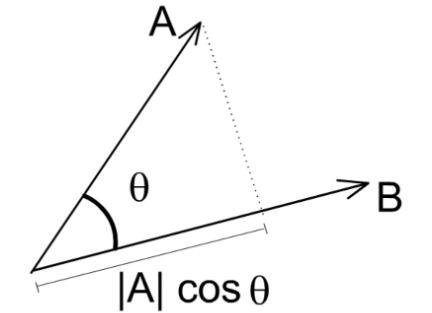
• 基于点乘结果可以判断这两个向量是否是同一方向，是否正交垂直，具体对应关系：

     点乘 > 0：向量夹角在0~90°之间
     点乘 = 0：正交，相互垂直
     点乘 < 0：夹角在90~180°之间
  

• 公式推导

  1. 向量c = a - b
  2. c^2 = a^2 + b^2 - 2abcos(theta)
  3. (a - b) ▪ (a - b) = a^2 + b^2 – 2a▪b = a^2 + b^2 - 2abcos(theta)
  

2. 叉乘

• 叉乘 = 叉积 = 外积 = 向量积

• cross product = outer product

• $\vec{a}=(x_1,y_1,z_1)$，$\vec{b}=(x_2,y_2,z_2)$

• 从代数角度计算：

  $$\vec{a}\times \vec{b}=(y_1{z}_2-y_2{z}_1,-(x_1{z}_2-x_2{z}_1),x_1{y}_2-x_2{y}_1)$$

• 从几何角度计算

  • 其中$\vec{i}$、$\vec{j}$、$\vec{k}$分别是x轴、y轴、z轴方向的单位向量
  • 当$z_1$、$z_2$等于0的时候，即得到二维向量叉乘的结果

$$\vec{a}\times \vec{b}=\left|\begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ x_1& y_1& z_1\\ x_2& y_2& z_2\end{array}\right|=(y_1{z}_2-y_2{z}_1)\vec{i}-(x_1{z}_2-x_2{z}_1)\vec{j}+(x_1{y}_2-x_2{y}_1)\vec{k}$$

• 叉乘的几何意义：

  • 二维向量叉乘：向量a和向量b的叉乘表示向量a和b构成的平行四边形的面积
  • 二维向量叉乘：如果a或b其中一个为单位向量，则axb叉乘结果表示以单位向量为底的平行四边形的高，可以有正负
  • 三维向量叉乘：向量a和向量b的叉乘结果是一个向量，该向量垂直于向量a和b组成的平面，即平面的法向量，方向遵守右手定则

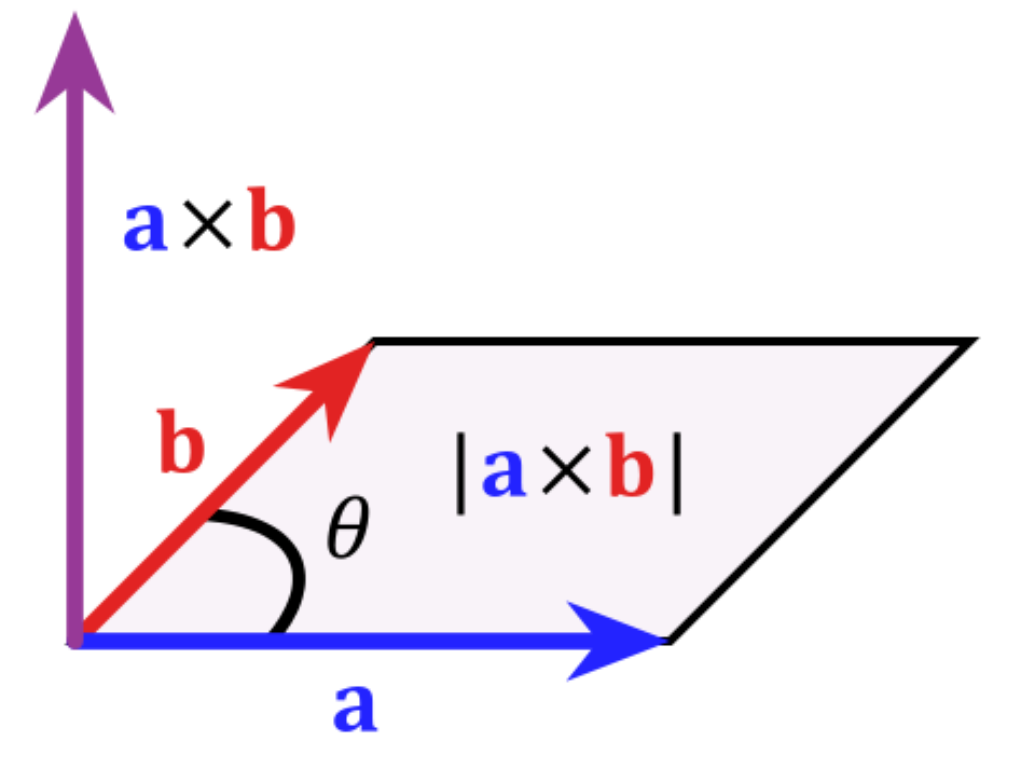
• 叉积有一个非常重要的性质，可通过叉积的符号来判断两向量的顺逆时针关系

  P x Q > 0, 则向量P在向量Q的顺时针方向；
  P x Q < 0, 则向量P在向量Q的逆时针方向；
  P x Q = 0，表示P与Q共线，可能同向也可能反向
  

3. 点乘 vs 叉乘，对比与应用

• 点乘的结果是标量(常用于物理)/数量(常用于数学)，可以用来计算夹角和投影
• 叉乘的结果是矢量(常用于物理)/向量(常用于数学)，法向量的模大小为$\left|a\right|\left|b\right|\sin \theta$，方向遵守右手定则
• 在二维空间中，叉乘结果等于向量a和b构成的平行四边形的面积，平行四边形的面积：以$\left|b\right|\sin \theta$为高，以$\left|a\right|$为底。当a是单位向量时，计算b的终点到a所在直线的距离，也就是平行四边形的高
• 通过向量的叉乘生成垂直于向量a/b的法向量，从而构建XYZ坐标系
• 叉乘的结果再点乘可以用来判断向量/线段是否相交，即”跨立实验”，见文章判断两条线段是否相交

《参考文章》

点乘叉乘及其几何意义
点乘叉乘的概念与几何意义
向量的顺逆时针关系

created by shuaixio, 2022.12.27

今天的文章点乘积和叉乘积的区别_向量积与数量积的区别分享到此就结束了，感谢您的阅读。