codeforces 洛谷_k2,3生成树的个数

一、题目描述

如题，已知一个数列，你需要进行下面两种操作：
1.将某区间每一个数加上x
2.求出某区间每一个数的和

输入格式
第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数，表示一个操作，具体如下：
操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k
操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式
输出包含若干行整数，即为所有操作2的结果。

输入输出样例
输入 #1

5 5
1 5 4 2 3
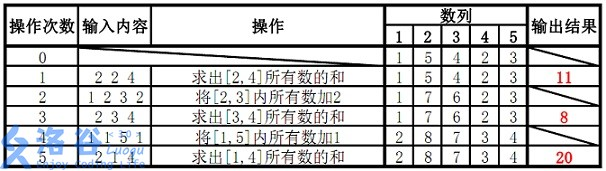
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出 #1

11
8
20

说明/提示

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强，保证在int64/long long数据范围内）

样例说明：

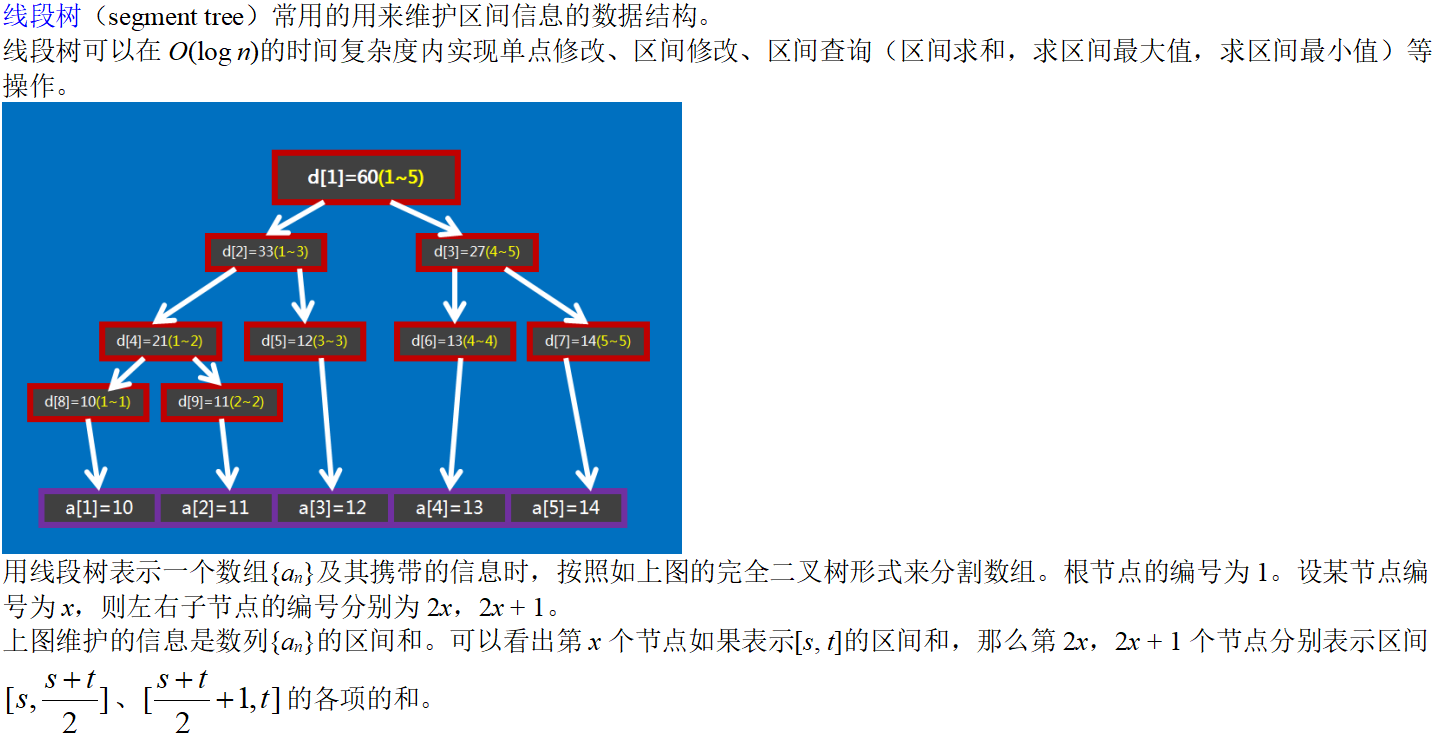
二、算法分析说明与代码编写指导

三、AC 代码

#include<cstdio>
#pragma warning(disable:4996)
template<class _Ty> class segment_tree { 
   
private:
	_Ty* a, * b, * lazy, v; size_t n, Size, L, R;
	_Ty get_sum(const size_t& s, const size_t& t, const size_t& r) const { 
   
		if (s >= L && t <= R)return b[r];
		_Ty m = (s + t) / 2, sum = 0, r0 = 2 * r, r1 = r0 + 1;
		if (lazy[r]) { 
   
			b[r0] += lazy[r] * (m - s + 1), b[r1] += lazy[r] * (t - m),
			lazy[r0] +

今天的文章codeforces 洛谷_k2,3生成树的个数分享到此就结束了，感谢您的阅读。