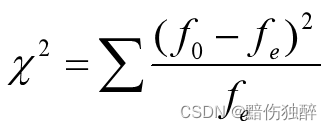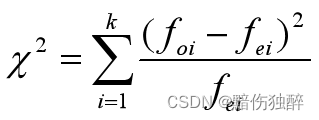第六节交叉分析和非参数检验的区别_交叉检验一般分为

第六节交叉分析和非参数检验

交叉分析

交叉分析（卡方检验）：

交叉分析又称为卡方检验，卡方检验的地位等同于独立样本t检验和单因素方差分析，目的也是为了研究变量之间的差异关系。是现状分析内容中的主要构成部分。卡方检验是专门进行分类变量之间差异性检验的主要分析方法。独立样本t检验和单因素方差分析解决了连续型随机变量的检验问题，而卡方检验解决分类变量的差异问题。因此这三种分析方法就构成了差分析分析部分的主要内容。

卡方检验的原理：

卡方检验公式：

f0代表实际的观测频数，而fe代表理论的频数。卡方值代表实际值和理论值之间的偏离程度。偏移越大说明差异越明显。

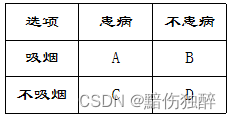
A、B、C、D代表实际频数

第一步计算概率：
患病概率=（A+C）/（A+B+C+D）
不患病概率=（B+D）/（A+B+C+D）
第二步计算理论频数：
A11=(A+B)(（A+C）/（A+B+C+D）)
A12=(A+B)(（B+D）/（A+B+C+D）)
A21=(C+D)(（A+C）/（A+B+C+D）)
A22=(C+D)(（B+D）/（A+B+C+D）)
第三步带入卡方计算公式计算卡方值。

卡方检验的假设及形式：

原假设：f0=fe（实际频数=理论频数）
备则假设：f0≠fe

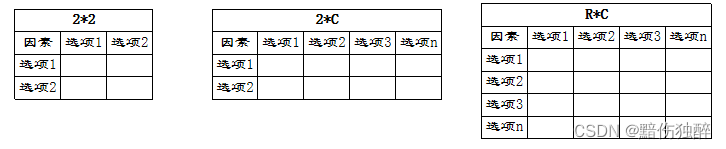
根据参与分析的分类变量选项的不同卡方检验可分为22，2C以及R*C三种形式。

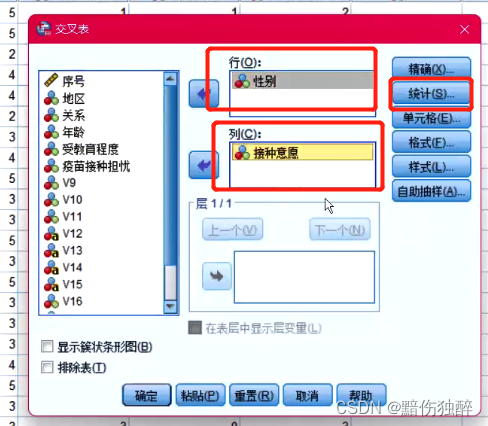
在检验中一般行为分组变量，列为检验变量（目标因素）。

案例：

2*2案例：
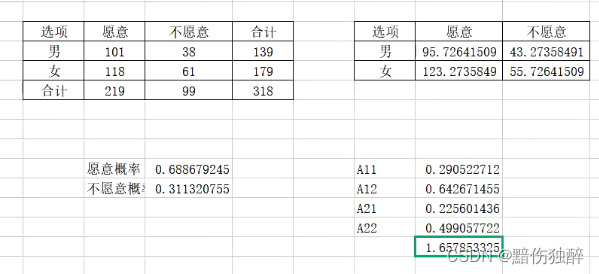
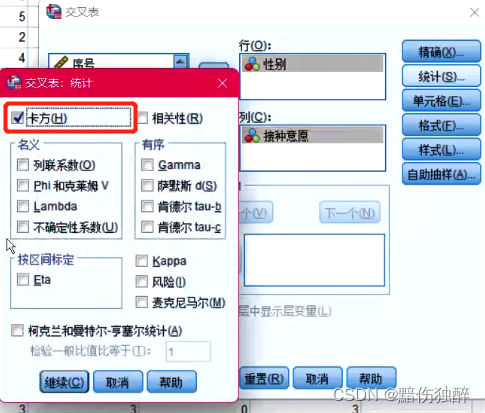
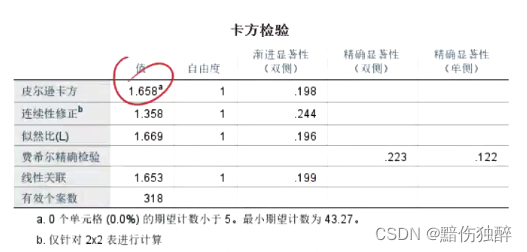
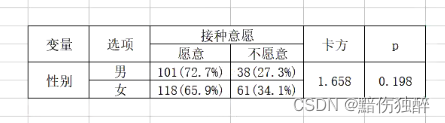
现开展了一项关于居民疫苗接种意愿调查的项目。通过问卷的形式进行了数据收集，最终一共采集了318份数据。现在想要了解不同性别的群体在疫苗接种意愿上是否一致。请根据实际的数据情况，选择合适的统计学分析方法对该需求进行分析。

显著性0.198大于0.05不能拒绝原假设，所以男女意愿没有差别

2*C案例：
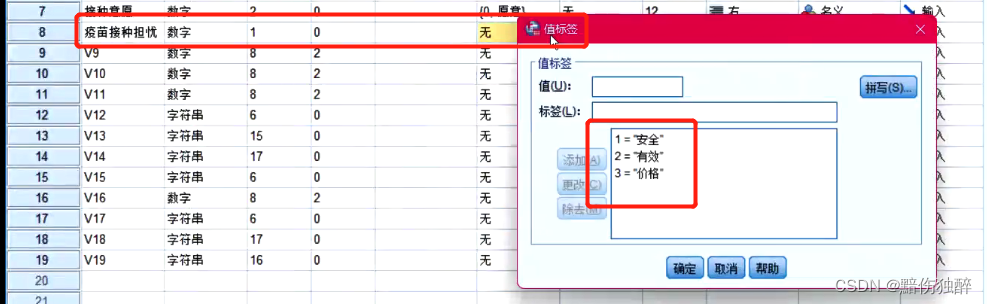
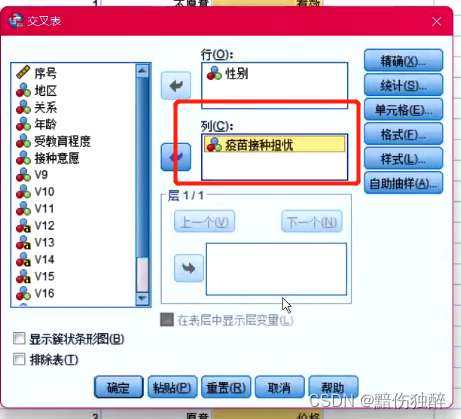
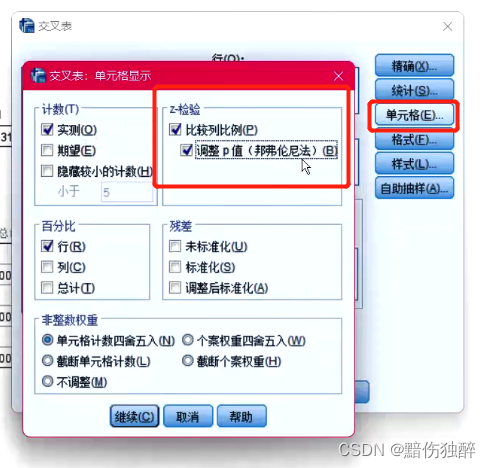
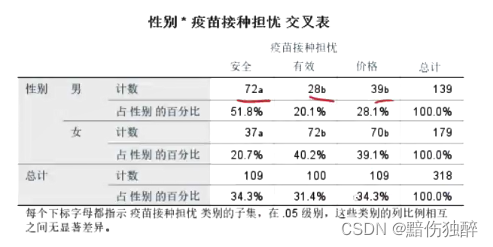
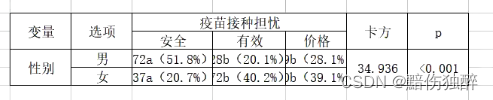
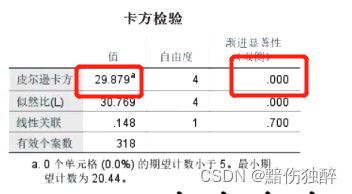
在疫苗接种意愿调查项目中，为了进一步提高居民的接种率，因此调查了对于疫苗担心的问题。现在要求更加精确的了解不同性别在疫苗接种上所担心的问题，从而根据结论制定对应的方案。因此，要求采用合适的统计学分析方法对该需求进行分析。

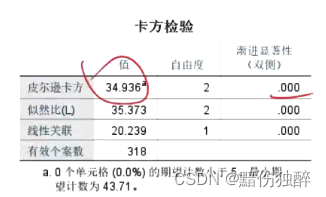
显著性p小于0.01，故不同性别在疫苗接种担忧是有显著性差异的。

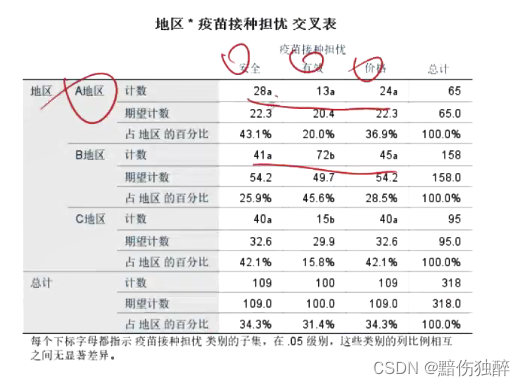
尾标a与b代表有差异，实际大于期望，男性更看重安全，女性更看重有效和价格

R*C案例：
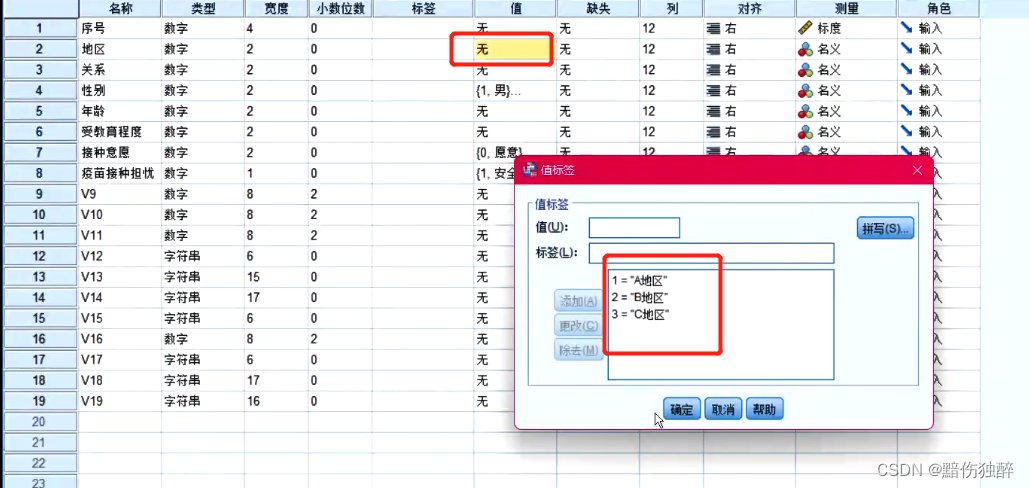
在前面的案例中我们了解了不同性别群体的接种意愿情况和担忧问题。在本次的调查中样本分别来自A地区、B地区和C地区。现在根据上级要求，还需要知道三个地区在疫苗接种担忧问题上是否有差异。请根据需求采用合适的分析方法对该需求进行分析并最终提出合适的建议。

A地区不存在差异，B地区更担心有效性，C地区有差异更担心安全和价格。

非参数检验

非参数检验：
非参数检验也是现状研究中的构成部分。它和参数检验是对应的，参数检验都是事先清楚数据的分布形态（满足正态分布），但是在现实中有的数据可能并不是正态分布的，或者对数据的分析形态我们并不清楚。那么在这样的环境下，如果要进行差异分析。那么就可以采用非参数检验里面的检验方法进行检验。

卡方检验（非参数检验法）

作用:非参数检验里面的卡方检验是用来检验分类变量的实际频数是否符合某种指定的分布形态。

公式：

其中foi为实际观测结果，fei为理论观测值。

案例：

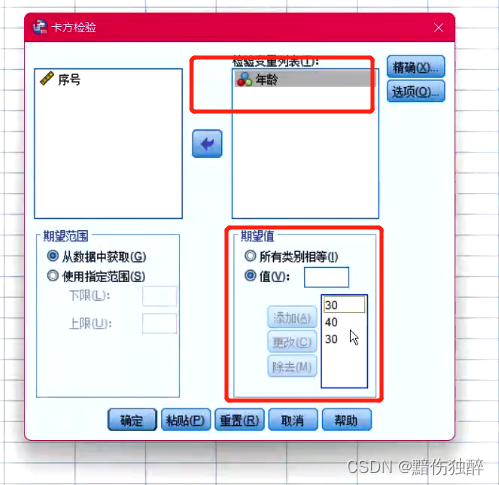
人口老年化是时间发展中绝大可能出现的问题。根据国家普查结果可知，xxxx年年龄总体的机构比例为年轻群体约30%，中年群体约40%，老年群体为30%。现在采用随机抽样的方式收集了某个省份318个人的年龄数据。现请通过合适的分析方法分析该省份的年龄结构是否和总体的结构一致。

不显著，不能拒绝原假设。

单样本k-s检验：

作用：单样本k-s检验是用来检验数据的分布形态的，通常用来检验数据是否满足正态分布。这是和单样本t检验最大的区别。单样本k-s检验不是用来检验差异性的。

原假设:实际收集的数据和我们指定的某种分布形态一致（通常指定正态分布）
备则假设：实际收集的数据分布形态和指定形态不一致。

案例：
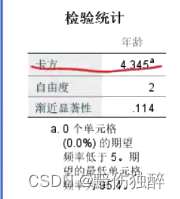
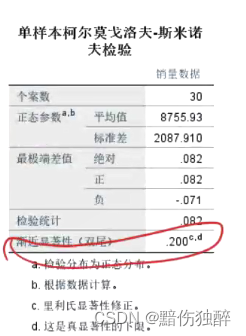
现收集了30个地区某产品的销量，请分析该产品的销量数据是否满足正态分布。
第一种方法：

注意在探索的方法里只能检验正态分布。

第二种方法：ks检验

可以检验四种分布，一般只是做正态性检验。

不拒绝原假设，则满足正态分布。

（注意：当样本k-s检验不仅仅适用连续型随机变量，还可以对分类变量，等级资料的分布形态进行检验。）

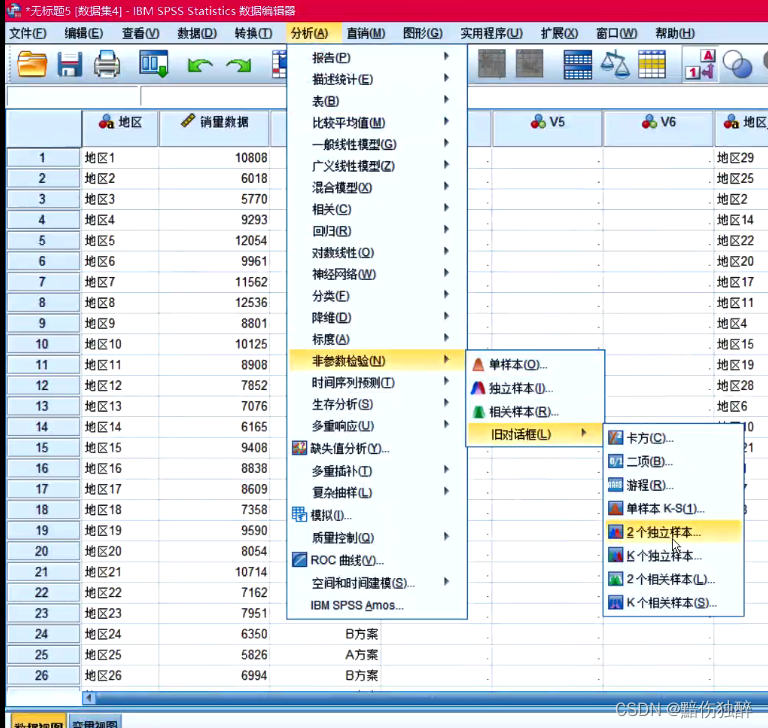
两独立样本检验：

作用：用来检验未知分布形态的数据是否来自总体分布相同的总体。和独立样本t检验有本质的区别。独立样本比较的是正态分布条件下，两组数据的均值是否相等。而非参数检验的原理是比较两组未知分布的数据是否来自分布相同的两个总体。（不要求数据为连续型随机变量）

原理：非参数检验进行两组或者多组数据的差异比较，由于不知道数据的分布形态。因此就没有办法在正态分布区间内构建置信区间然后进行均值的比较。因此，在非参数检验里面都是去推断两组或者多组数据是否来自相同分布的总体，这里的分布就不是只正态分布，而是其他任意可能的分布均有可能。而在推断样本组数据来源什么分布的时候采用的是“秩和”检验的原理。（秩是排序，和是加法）
秩和检验的原理在实现过程上分为三个步骤：
第一步：将实际收集的多组数据合并，然后按照升序进行排列。
第二步：排列完后，样本里面的每一个数据都有了自己特定的排名。然后再将两组数据分开。
第三步：观察两组数据秩的排名，计算秩和然后选择对应的分析方法计算显著性p值。

两独立样本检验：
在两独立样本中计算原假设成立的概率p值得方法有四种：
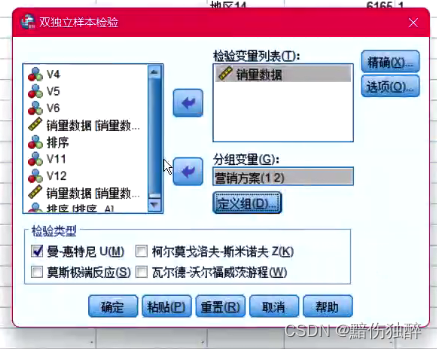
1、Mann-Whitney U检验
2、Kolmogorov-Smironv Z检验
3、Moses 极限反应检验
4、Wald-Wolfowitz游程检验
这四种检验方法都是用来检验多组数据之秩和是否有差异的方法，每种方法的计算原理不同，类似于单因素方差分析的多重比较有很多种检验方法，最常用的是LSD。在秩和检验里面也是类似，这四种检验方法里面最常用的是第一个Mann-Whitney U检验。

案例：

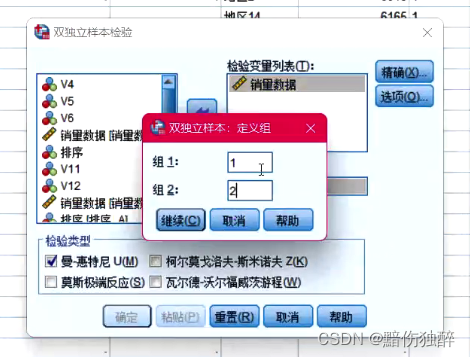
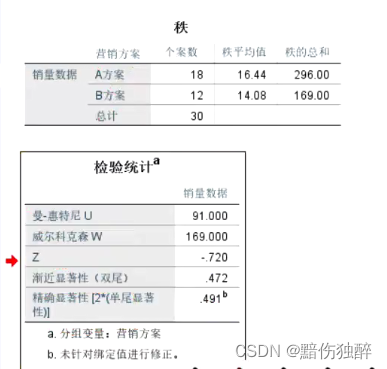
某企业采用随机采用两种营销方式在30个地区进行产品的推销。经过一段周期的方案实施以后，收集对应的销售数据。现要求采用合适的统计学分析方法对两种营销方案的销售结果是否有差异进行分析。
解析：类似的案例，如果数据满足正态分布或者中心极限定理能做为支撑就就应该采用独立样本t检验进行差异分析。这里我们假定销售数据确实不满足正态分布。因此就需要采用非参数两独立样本进行检验。

原假设：H0:营销方案1的销售数据和营销方案2的销售数据服从相同的分布
H1:营销方案1的销售数据和营销方案2的销售数据不服从相同的分布

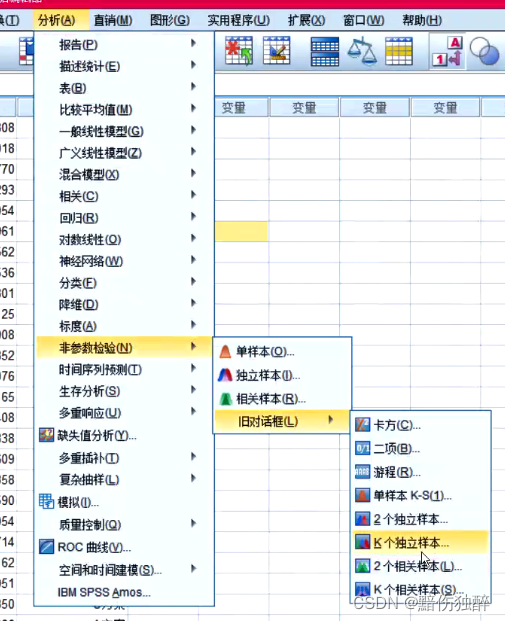
k个独立样本检验：

作用：k个独立样本作用类似于单因素方差分析，都是用来检验多组数据之间是否存在差异的分析方法。

原理：k个独立样本进行差异检验的原理和两独立样本检验的原理一样。都是基于“秩和”进行检验。

原假设：H0:k个独立样本所代表的总体满足相同的分布形态。
H1:K个独立样本所代表的总体不完全满足相同的分布形态。

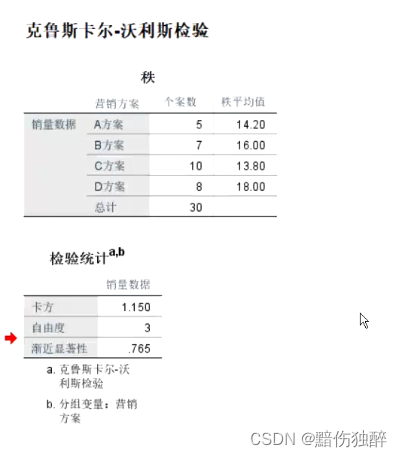
案例：

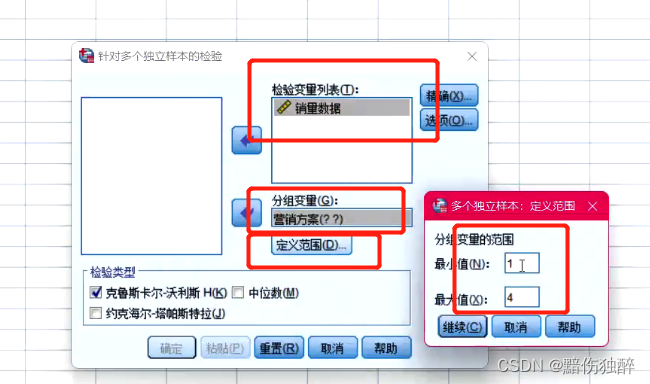
某企业采用随机采用4种营销方式在30个地区进行产品的推销。经过一段周期的方案实施以后，收集对应的销售数据。现要求采用合适的统计学分析方法对两种营销方案的销售结果是否有差异进行分析。
解析：类似的案例，如果数据满足正态分布或者中心极限定理能做为支撑就就应该采用独立样本t检验进行差异分析。这里我们假定销售数据确实不满足正态分布。因此就需要采用非参数两独立样本进行检验。

原假设：H0:4种营销方案销售数据服从相同的分布
H1:4种营销方案的销售数据不完全服从相同的分布