【报告】Fast Few-Shot Classification by Few-Iteration Meta-Learning（FIML）

报告文章来源于ICRA 2021，题为 Fast Few-Shot Classification by Few-Iteration Meta-Learning， 通过少量迭代的元学习实现的一种快速小样本分类方法 ，作者来自瑞士苏黎世联邦理工学院计算机视觉实验室。

内容分为以上5个部分

few-shot classification 是要在仅给出少量带标注样本的情况下学习分类器。

meta-learning 元学习，从学习解决其他类似任务中获得经验，以便更好地学习目标特定的任务

现有的元学习方法可以分为两类。 基于度量的、和基于优化的。

基于度量的方法，是在其他任务上学习一个嵌入空间，利用目标任务在该嵌入空间上的特征距离，来进行标签的估计。
基于优化的方法，是在经过其他任务学习后的模型的基础上，对参数进行优化，使其能适应目标特定任务。

本文的方法，属于后者。 以上是文章作者，给出相关背景的解释。

下面，我结合元学习的数据集构造来给大家介绍一下元学习以及我们常说的C-way k-shot问题。
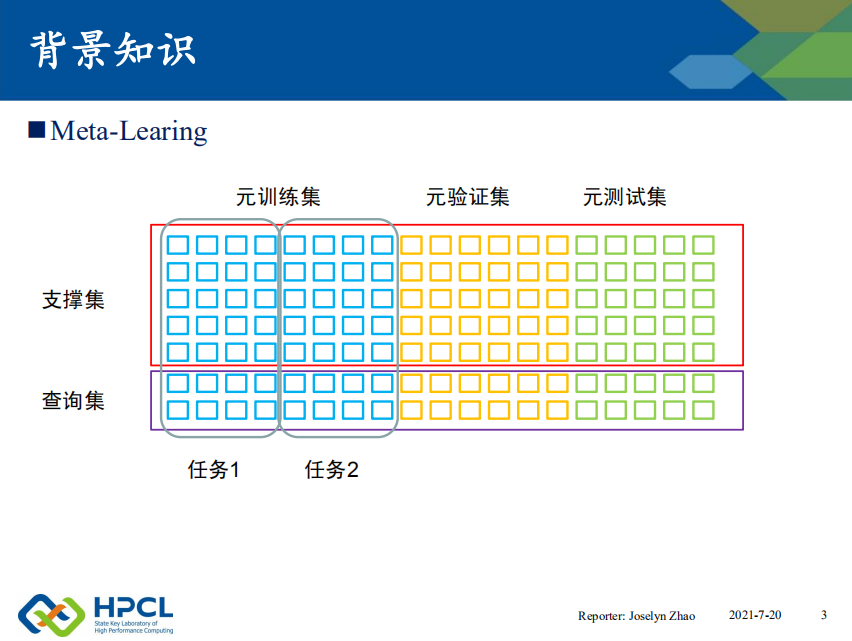
我们用这些小方块来表示样本，同一列是同一个类别，我这里没有用省略号来表示，真实的数据集的类别数量和样本数量都远不止这个规模。
下面我们以类别为单位，划分出元训练集、元验证集和元测试集，这一点呢，和传统的深度学习数据集是一样的，验证集用来在训练过程中评估性能，测试集用于评估模型最终的泛化性能。
不一样的地方是，我们以元训练集为例，我们从中选了4个类别组成一个任务，我图上画了两个没有类别重复的两个任务，实际上，这里可以构成$C_8^4$个任务。
接下来，我们在每个任务中，从每个类别中选出5个样本来构造支撑集，剩下的样本构成查询集。 这样的数据集就是一个4-way 5-shot的元学习数据集

本文方法的出发点有两个。 一个提高分类准确率，二是减少训练所需的时间。

文章主要提出了一种迭代的基于优化的元学习方法， 简称FIML。
这个方法的框架包含了两个部分： 是一个嵌入网络，一个是base学习器，嵌入网络是用来提供输入图像的特征表达的，base学习器通过展开优化程序在推断过程学习线性分类器。

训练的目标函数主要两个部分损失组成，一个是支撑集上的分类损失，另一个是允许从未标记的查询样本进行直推学习的交叉熵损失。 这两个目标分别是后文提到 inductive loss 和 transductive loss

在训练策略和算法方面：文章应用了一个有效的初始化模块 ，采用的是基于最速下降的优化算法。

文章方法在四个数据集上对 速度和 效果进行了验证，结果表明，FIML创造了基于优化的元学习领域新的state of the art 性能。

作者自评，本研究首次在基于优化的元学习框架中将归纳和传导结合到base学习器中

对于任务T，他由支撑集和查询集两部分数据构成。查询集是那些需要被分类，且只给出了少量标记的图像样本的数据，x都表示图像样本，y表示标签。 N
= k x n 表示的是样本-标签对的数量，k x n的含义是 有k个类别，每个类别有n个样本，所以这里是 k-way， n-shot分类问题。

前面我们说方法框架主要包含了两个模块嘛，一个是base 学习器，还有一个是元学习器，他们分别可以用公式1和2来表示。其中D表示整个元训练集，它包含了很多个任务，元学习是希望学习一个通用的网络参数 $\varphi \ast$，使得在大多数任务上表现得很好，而base 学习器是针对任务T来进行学习的。

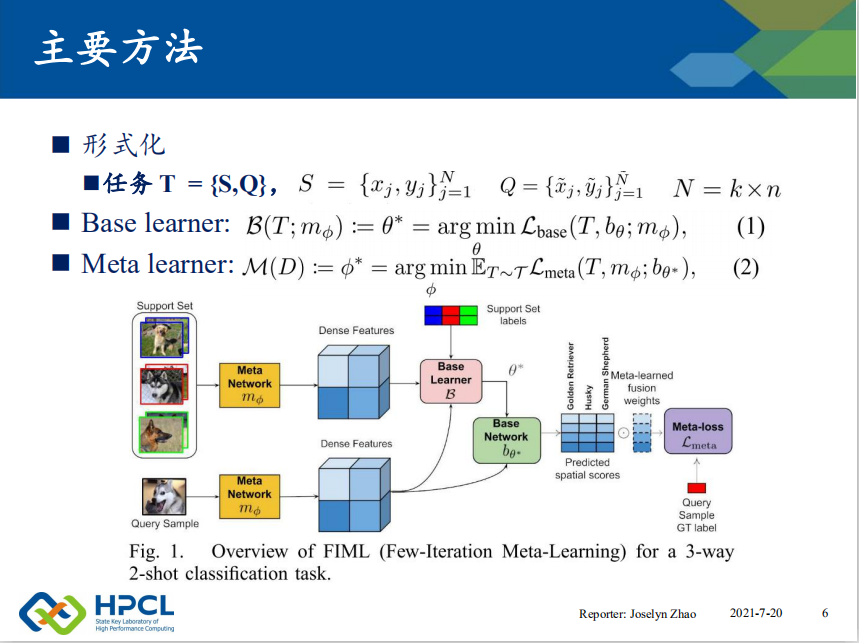
如1 展示了FIML的框架，这是一个3-way 2-shot的分类任务。 体现在支撑集包含3个类别，每个类别2张图像。元学习器提供特征表示，Base 网络对查询的图像进行分类。
每次训练输入的是 6张支撑集图像和1张查询集图像， 模型回答了 查询图像是 三个类别中的哪个类别的问题。

在inductive 损失中，对于任务T，我们要学习base分类器的参数 $b_{\theta }$，
base 网络对样本x的预测用$b_{\theta }(m(\varphi (x))$来表示。
base 学习器的目标函数，根据给出的支撑集样本标签和base学习器的预测结构求损失， 如公式3所示。 其中，r可以是一般的残差函数，文中，r被定义为公式4。。
其中， zj = 2倍标签-1，$sj=b_{\theta }(x_j)$ ，表示学习器的预测结果。 $l_j$由两个部分组成，其中l+和l- 分别为正类和负类的目标回归得分，分别为正类和负类定义了分类器的边界。 $a_j$也由两个部分组成，其中(a+和a−)和目标回归分数(l+和l−)是我们的base损失公式中的自由参数，使得损失具有更强的自适应性和鲁棒性。

我们虽然不知道 查询图像属于那个类别，但很明确的是 它只可能属于一个类别，所以这构造了一个约束，可以用来作为目标函数。
在本文的工作中，我们惩罚查询样本上预测的香农熵，促进Base学习器来寻找对查询集可靠的分类参数。

transductive 项 表示为 所有查询样本分类概率的香农熵之和，公式5 的推导是代入pj = softmax的过程。
这里sj不一样的是增加了一个温度尺度参数beta。sjc 是属于类别c的分量。

最终的目标函数是 如公式6所示。
两个lambda值都是权重。

下面是base学习器的优化。 优化迭代可以表示为 公式7所示。
其中，${\alpha }^{(d)}$是步长，d表示迭代的次数。

为了进一步较少公式7所需要的迭代步数，文章提出了有效的初始化策略 来获取${\theta }^0$

${\theta }_c^0=k^c{f}_{pos}^c–{\tau }^c{f}_{neg}^c$。从正样本和负样本两方面进行考虑，文中也给出了 $f_{pos}^c$ 和$f_{neg}^c$ 的计算，其中大 N为 任务T的支持集S中的样本数。n为n-shot的n的大小。

Dense 分类这部分内容通过整合Dense分类策略，利用不同空间位置提取的样本，进一步解决了标记数据的缺失问题。
文章在全局平均池化层之前 使用Dense的空间特征，用m phi l表示空间索引L处的特征向量。 这个策略允许我们从多个区域样本中学习，我们的任务是为每个查询图像生成一个最终的预测结果。
这将通过一个 空间融合程序实现，如公式8所示。 预测分数sj 由 各个空间位置的预测结果加权求和得到，
其中， { v l } \left\{v_l\right\} {
vl​} 是元训练中学习到的空间权值的集合，表示对某个空间位置，base网络的预测结果给予了多大的重视。

在元训练阶段，我们最小化任务中查询样本的概率向量的交叉熵 为公式9所示，其中，$p_j$还是等于softmax（sj）。

文章实验用pytorch框架实现。对miniImageNet和tieredImageNet这两个较大的few-shot分类数据集进行了消融研究

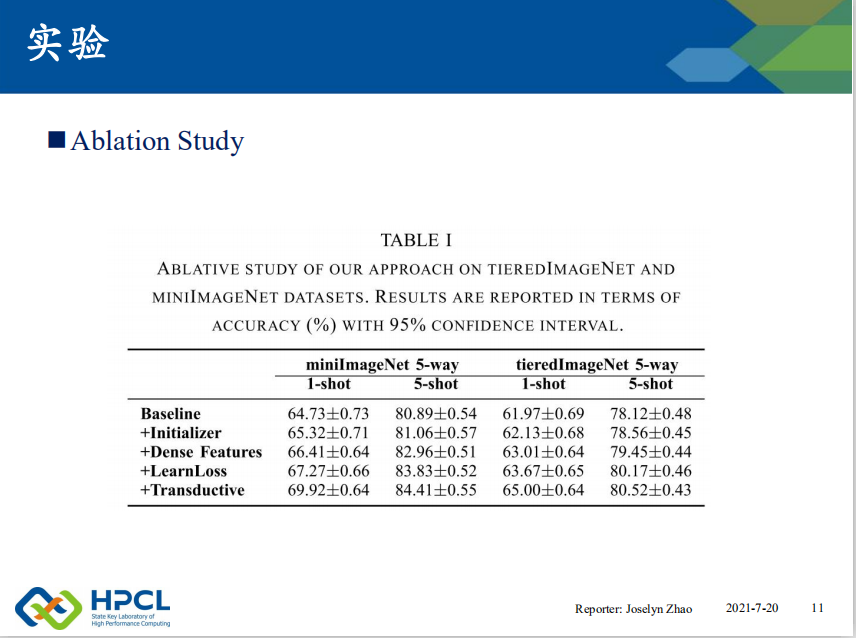
表1是 ablation study的实验结果。分别测试了本文提出了各个模块逐一加入后的效果。
可以看出，每个模块的加入，都为性能的增长做出了贡献。

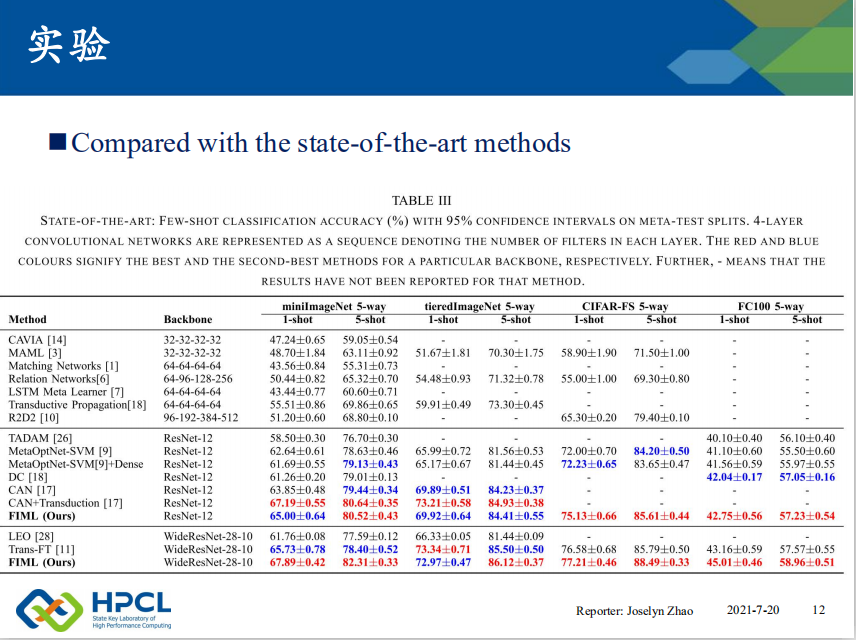
实验结果表明，本文的方法明显优于其他方法。值得注意的是，当使用相同的ResNet-12作为骨干网络时，我们的方法在更大的tieredImageNet数据集上的1-shot和5-shot性能分别实现了3.6%和2.4%的相对改进。
此外，本文的框架可以利用更广泛的目标函数类，可以元学习目标和base学习器本身的重要参数。

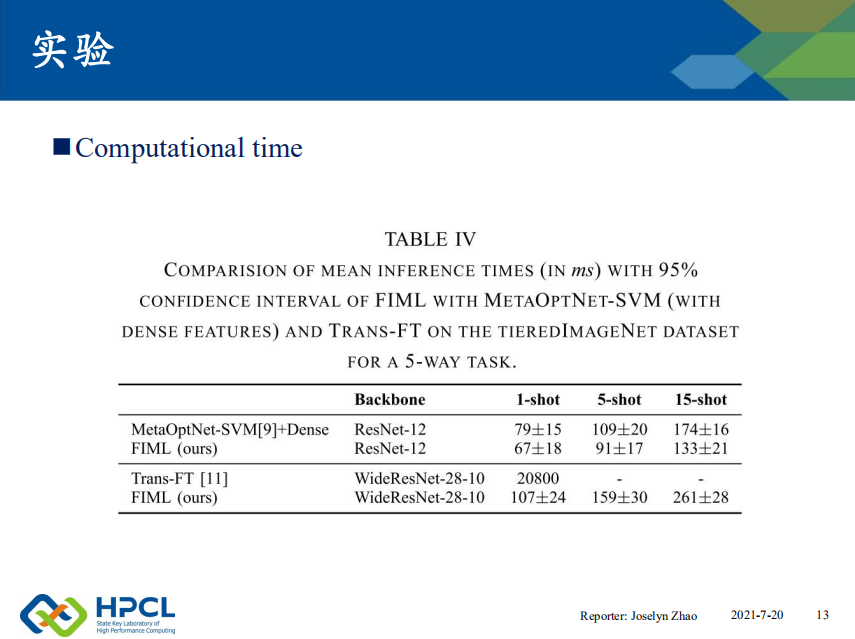
文章还在tieredImageNet上 比较了FIML 和 MetaOptNet+Dense 方法的计算时间。
表4 以毫秒(ms)为单位， 显示了 1-shot、5-shot，15-shot任务的时间。很明显，FIML比MetaOptNet+Dense在推理过程中计算得更快。。。

至于Trans-FT，我们可以看到在tiredImagenet的上的性能方面，与本文是不相上下的，我们的方法在5-shot的情况下优于Trans-FT，但在1-shot的情况下，性能略有下降。
但是，计算时间上，我们的方法比trans-TF快了200倍。他用时 20800ms 也就是是 20.8 s，而本文方法仅用了 107 ms

总结一下，这篇文章在few-shot分类性能和计算时间两个方面都取得了进步，采用的是基于优化的元学习方法。 文章将Dense特征与一种新的自适应融合模块集成在few-shot的设置中。inductive和transductive 损失同时也被集成到框架中，迫使base网络对查询样本做出可靠的预测。此外，基于支撑集的线性base网络初始化有助于迭代展开优化器，使得base网络更快地收敛。

The Code is available at https://github.com/4rdhendu/FIML.

今天的文章【报告】Fast Few-Shot Classification by Few-Iteration Meta-Learning（FIML）分享到此就结束了，感谢您的阅读。