常用的参数检验和非参数检验方法对比图_参数检验的三个要求

1. 参数检验的集中趋势的衡量为均值，而非参数检验更适合为中位数，比如收入情况，如果在样本中加入几个亿万富翁，即使一般人的收入没有变化，平均值也会大幅度增加，但中位数没有显著差异。
2. 优缺点对比：1）参数检验：优点是符合条件时，检验效率高；其缺点是对数据要求严格，如等级数据、非确定数据不能使用参数检验，而且要求数据的分布型已知和总体方差相等。
   2）非参数检验：优点是应用范围广（没有正态分布的假设）、简便、易掌握；缺点是若对符合参数检验条件的数据用非参数检验，则检验效率低于参数检验。如无效假设是正确的，非参数法与参数法一样好，但如果无效假设是错误的，则非参数检验效果较差。
3. 当样本量足够大时，参数检验的方法对非正态分布的数据也能够很好地进行处理，因为样本均值的分布根据中心极限定理是近似正态分布。当样本量较小且分布未知时，通常会考虑使用非参数检验。
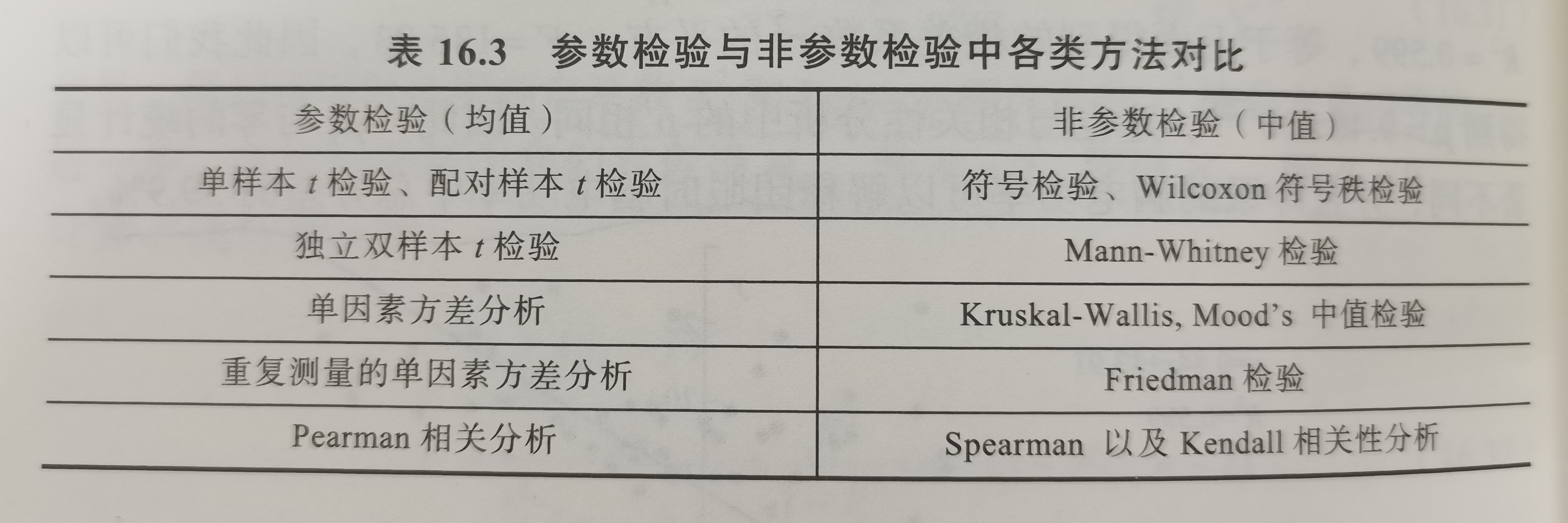
4. 各类方法对比：

三、具体方法对比

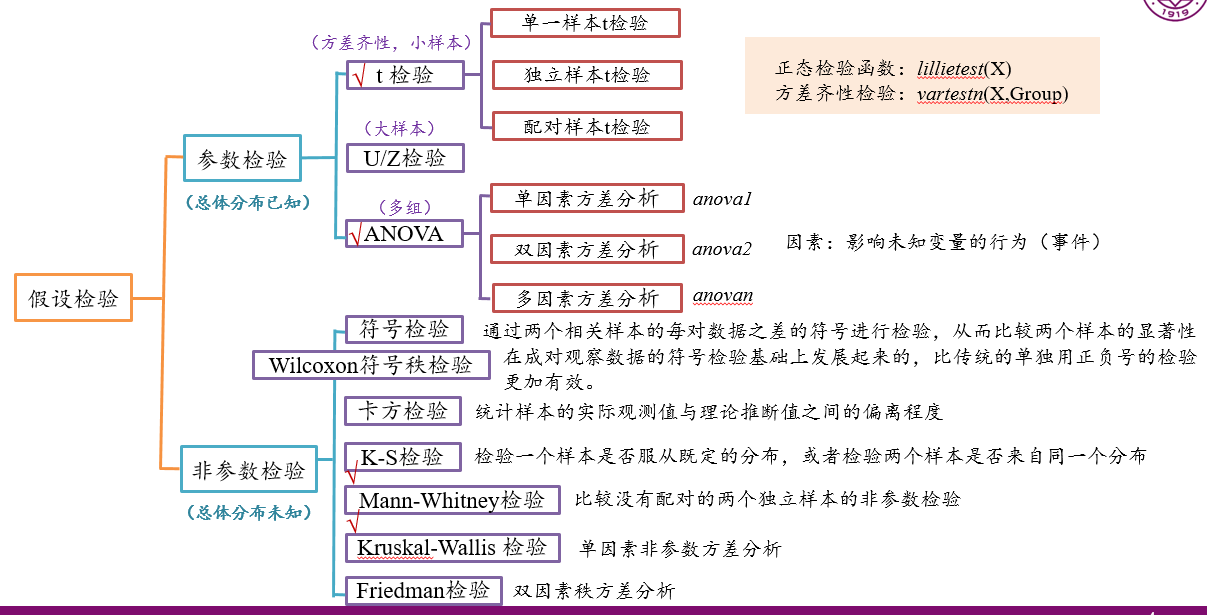
1、参数检验

1. t检验：它适用于计量数据、正态分布、方差具有齐性的两组间小样本比较。包括样本与均数间、两样本均数间、配对数据间的比较三种，分别对应的是单一样本t检验，独立样本t检验和配对样本t检验，三者的计算公式是不同的。T检验需要满足正态分布性和方差齐性，在不满足方差齐性时，需要使用t‘检验。
2. U检验，也称Z检验，应用条件与t检验基本一致，只是当大样本(N>30)时用U检验，而小样本(N<30)时则用t检验。
3. 方差分析：用于正态分布、方差齐性的多组间计量比较。常见的有单因素、双因素、多因素的均数比较，“因素”指影响未知变量的行为（事件）。方差分析首先是比较各组间总的差异，如总差异有显著性，再进行组间的两两比较。

我们提到不论是t检验还是方差分析必须满足两条假设，分别是正态性和方差齐性。因此，在一个完整的统计工程中，必须首先检测数据的正态性和方差齐性，matlab里有对应的函数可以直接调用，lillietest正态检验函数和vartestn方差齐性检验。

2、非参数检验

非参数检验我们一般用的不多，简单列举了几个，非参数检验检验的是分布而不是参数，所以总体分布是未知的。

1. 符号检验：符号检验还可用于配对样本的比较检验，符号检验法是通过两个相关样本的每对数据之差的符号进行检验，从而比较两个样本的显著性。具体地讲，若两个样本差异不显著，正差值与负差值的个数应大致各占一半。
2. Wilcoxon符号秩检验：符号检验只考虑的分布在中位数两侧的样本数据的个数，并没有考虑中位数两侧数据分布的疏密程度，这就使得符号检验的结果比较粗糙，检验功率较低。统计学家维尔科克森在1945年，提出了一种更为精细的“符号秩检验法”，该方法是在配对样本的符号检验基础上发展起来的，比传统的单独用正负号的检验更加有效。它适用于单个样本中位数的检验，也适用于配对样本的比较检验，但并不要求样本之差服从正态分布，只要求对称分布即可。
3. 卡方检验: 就是统计样本的实际观测值与理论推断值之间的偏离程度，以卡方分布为基础，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，卡方值越大，越不符合；卡方值越小，偏差越小，越趋于符合，若两个值完全相等时，卡方值就为0，表明理论值完全符合。
4.  K-S检验: 是基于累计分布函数的，检验一个样本是否服从既定的分布，或者检验两个样本是否来自同一个分布。
5. 曼·惠特尼检验，是比较两个独立样本的非参数检验。
6. K-W检验，又称“H检验”，用以检验两个以上样本是否来自同一个概率分布的一种非参数方法。被检验的几个样本必须是独立的或不相关的。与此检验对等的参数检验是单因素方差分析，但与之不同的是，K-W检验不假设样本来自正态分布。它的原假设是各样本服从的概率分布具有相同的中位数。
7. Friedman 福里德曼检验: 又被称之为双因素秩方差分析，是非参数版的anova2。同anova2一样，待检验的数据也必须是均衡的。但是福里德曼检验和anova2检验不完全相同，anova2同时注意两个因素对待检验数据的影响，但是，福里德曼检验只注重2个因素中的其中一个对待检验数据的影响，而另一个因素则是用来区分区组用的。（有4名美食评委1234对来自于四个地区ABCD的厨子做的烤冷面做出评价打分，现在我们想知道，这四个地方的烤冷面品质是否相同，那么同一个评委对四个地区厨师的打分就具有可参考性，而不同地区评委之间对同一个厨师的打分参考性几乎没有（受评委自己的主观意识影响太强）。因此，我们只考虑地区因素，而评委因素是区组因素，不同区组之间的数据没有可比较性。）