1. 二元函数的极值与驻点
例题
求函数 f ( x , y ) = x 3 − y 3 + 3 x 2 + 3 y 2 − 9 x f(x,y)=x^3-y^3+3x^2+3y^2-9x f(x,y)=x3−y3+3x2+3y2−9x的极值:
f x ( x , y ) = 3 x 2 + 6 x − 9 = 0 f_x (x,y)=3x^2+6x-9=0 fx(x,y)=3x2+6x−9=0
f y ( x , y ) = − 3 y 2 + 6 y = 0 f_y(x,y)=-3y2+6y=0 fy(x,y)=−3y2+6y=0
求得驻点为:(1,0),(1,2),(-3,0),(-3,2)
再求出二阶偏导数
f x x ( x , y ) = 6 x + 6 f_{xx}(x,y)=6x+6 fxx(x,y)=6x+6
f x y ( x , y ) = 0 f_{xy}(x,y)=0 fxy(x,y)=0
f y y ( x , y ) = − 6 y + 6 f_{yy}(x,y)=-6y+6 fyy(x,y)=−6y+6
对各驻点进行判断:
在点(1,0)处, A C − B 2 = 12 ∗ 6 > 0 AC-B^2=12*6>0 AC−B2=12∗6>0,又A>0,所以函数在(1,0)处有极大值f(1,0)=-5,
其他以此类推。
二、拉格朗日乘数法及条件极值
例1:
例2:
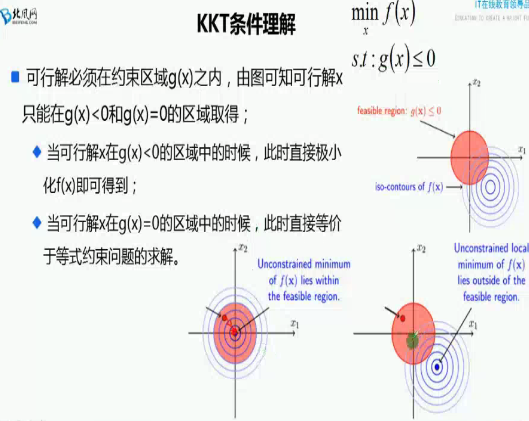
其实这道题是kkt条件的一个应用。
对于不等值约束,我们可以先计算二元函数的一个极值,判断极值是否在限制条件内(即求出来的极值点是否满足限制条件),如果是代表解在限制条件内部直接求极值,如果不是代表点在限制条件外部,则最小值一定是限制条件函数的边缘,此时相当于等值约束。
例2:如果我将限制条件改为 y > x 2 且 y > = x y>x^2且y>=x y>x2且y>=x此时题目怎么做
今天的文章二元函数求极值怎么求_高等数学求极值的步骤分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/82776.html