cnn代码详解_cnn代码详解

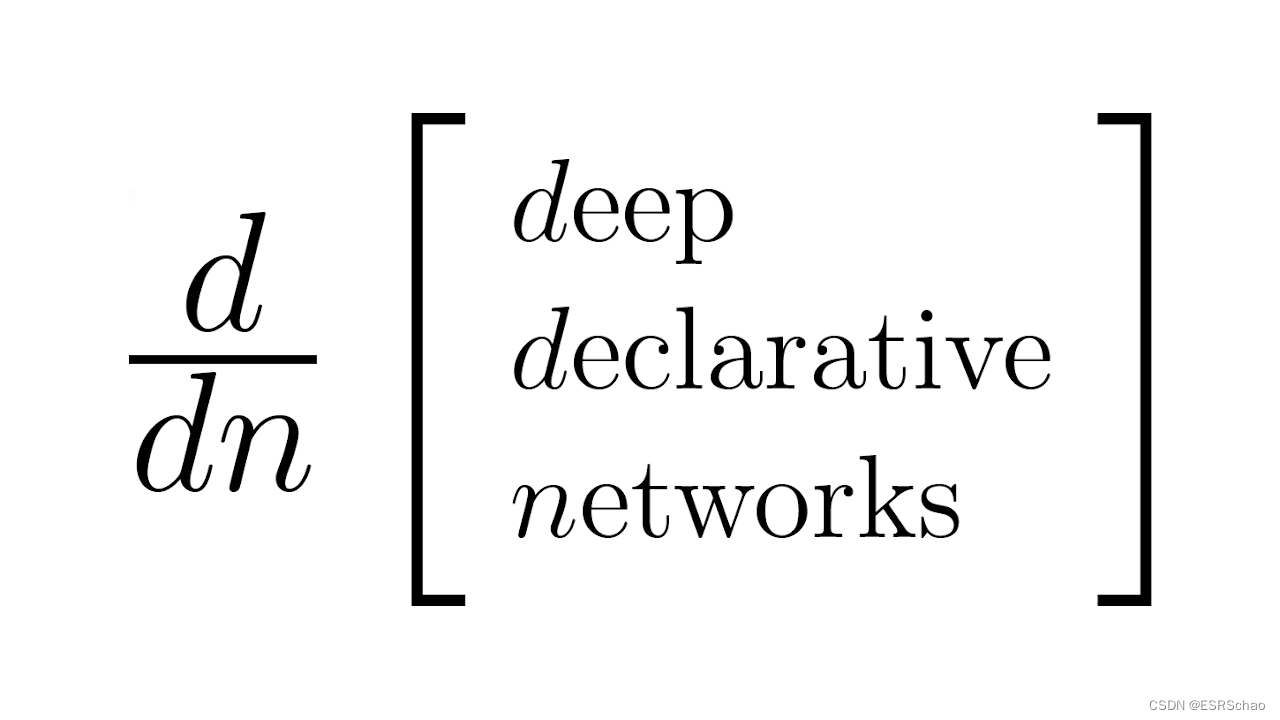
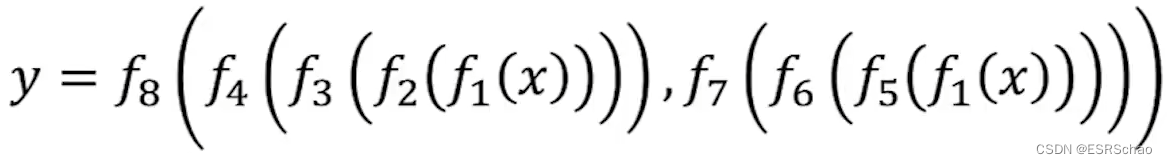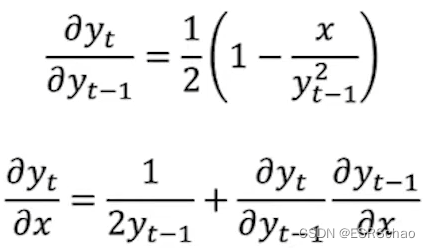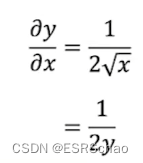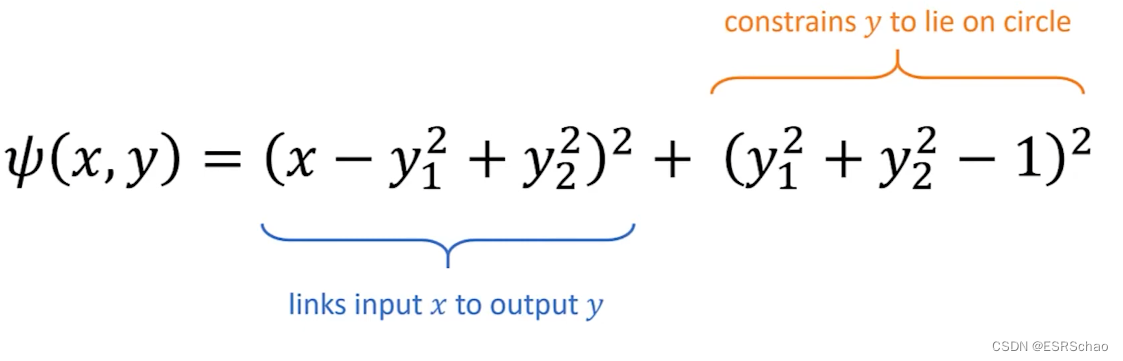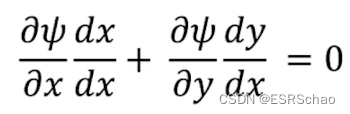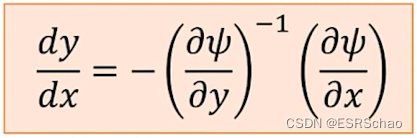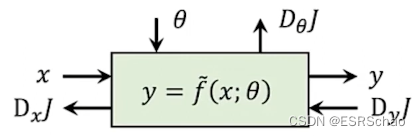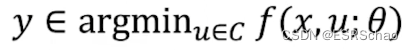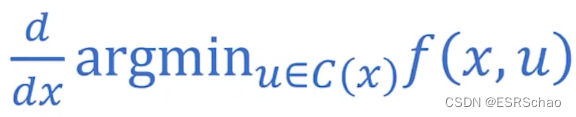写在前面

本系列笔记由笔者记录自Deep Declarative Networks开发团队在油管上发布的官方教程视频，有魔法的可以移步外网观看加深理解，链接如下https://www.youtube.com/watch?v=fnJIj906qoA

本系列教程中的所有公式和理论基于如下论文：
Gould, S., Hartley, R., Campbell, D.: Deep declarative networks: A new hope. Tech. rep., Australian National University (arXiv:1909.04866) (Sep 2019)
及其在2020ECCV发布的补充论文。

引子

传统的深度学习架构涉及简单且明确定义的前馈处理函数（内积、卷积、元素非线性变换和池化操作）的组合。在过去的几年里，研究人员一直在探索具有嵌入式可微优化问题的深度学习模型，最近这些模型已被应用于解决计算机视觉中的问题和机器学习的其他领域。

所以像这样在神经网络中出现优化部分的网络称为深度声明式网络（DDN）。重要的是，即使事先不了解用于求解优化问题的算法，也可以计算优化问题解相对于输入和参数的梯度，从而实现有效的反向传播和端到端学习。

主题

本教程将介绍DDN及其变体。我们将讨论可微优化背后的理论，专门的在开发此类模型以及将这些模型应用于计算机视觉问题时需要克服的问题。此外，本教程将提供设计和实现自定义声明性节点的实践。 教程主题包括：

• 声明式的端到端可学习处理节点。
• 可微凸优化问题。
• 计算机视觉应用程序的声明式节点。
• 实施技术和注意事项。

1. 神经网络基础知识

在第一章中我们将通过三个关键思想来了解DDN提出的动机与实现的具体细节。

1.1 神经网络模型（第一个关键思想）

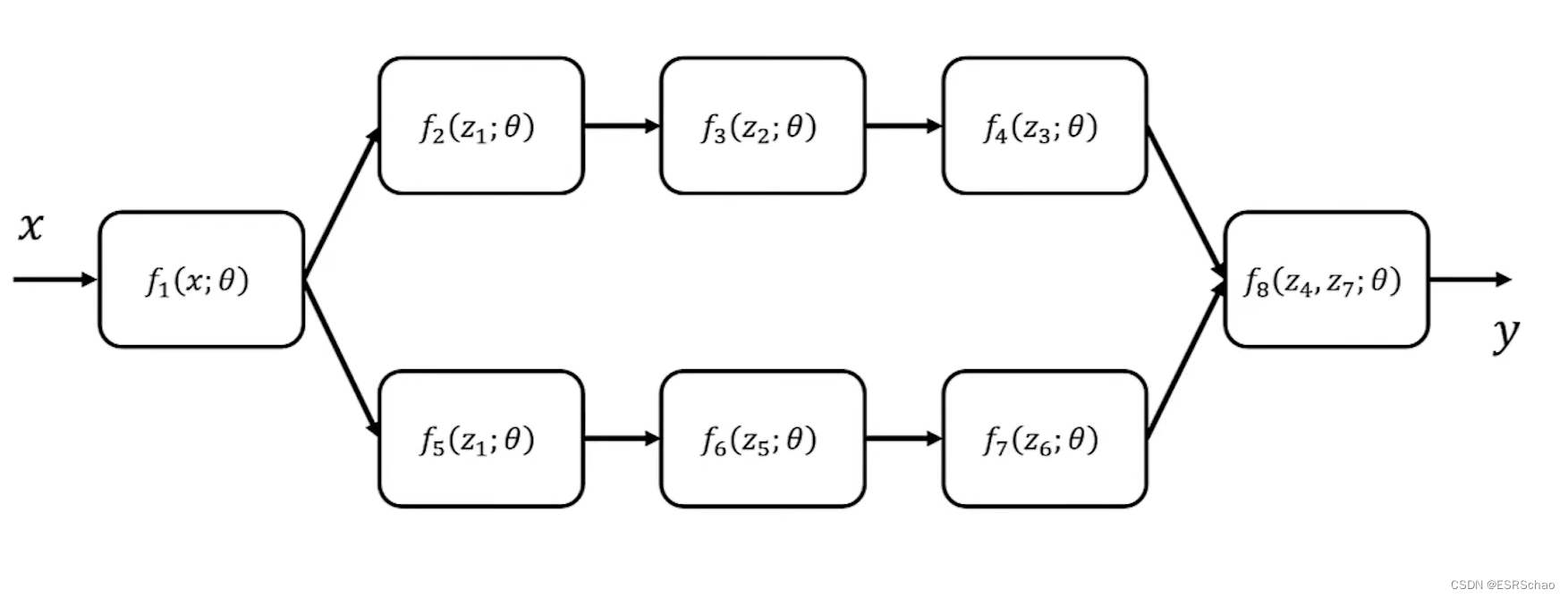
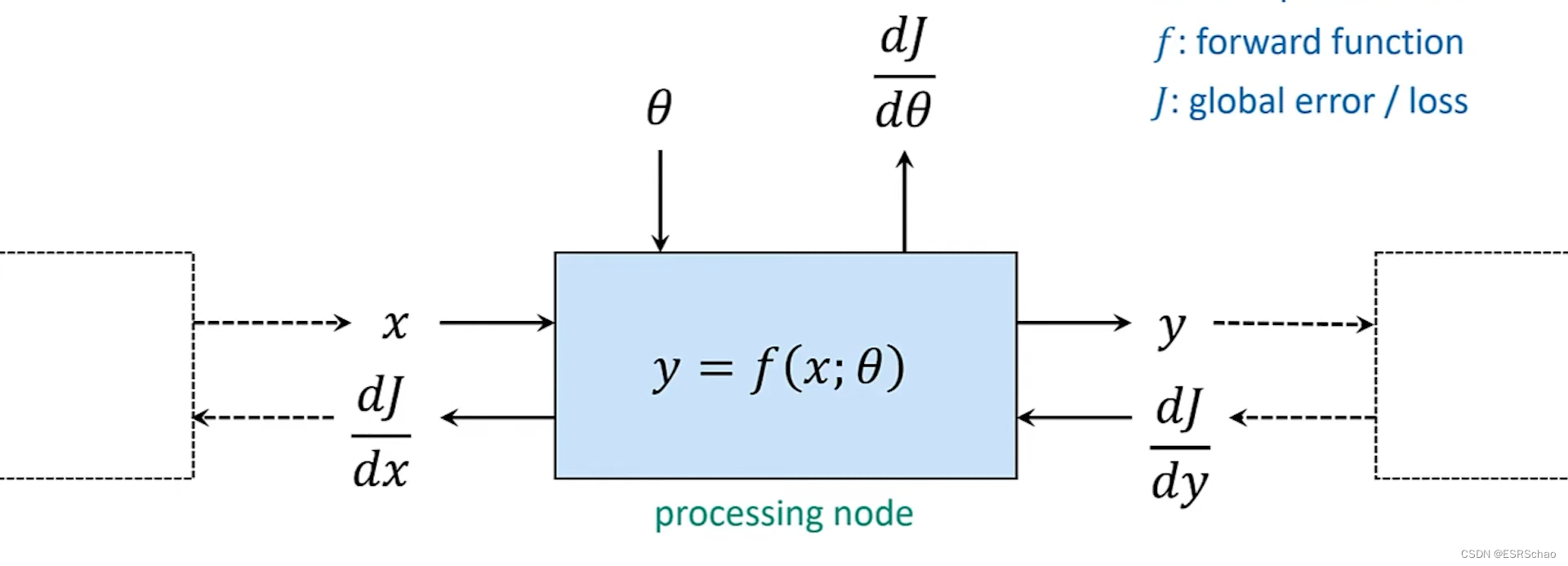
首先我们先从一个普通的一个学习模型或者深度神经网络开始，我们可以将其视为数据流图，它定义了神经网络中数据的存在形式以及它们如何在前向传播中进行处理，从而依次得出一些预测或者估计。

其中$f$是每个节点的函数表示，$\theta$是节点中可以更新的参数。
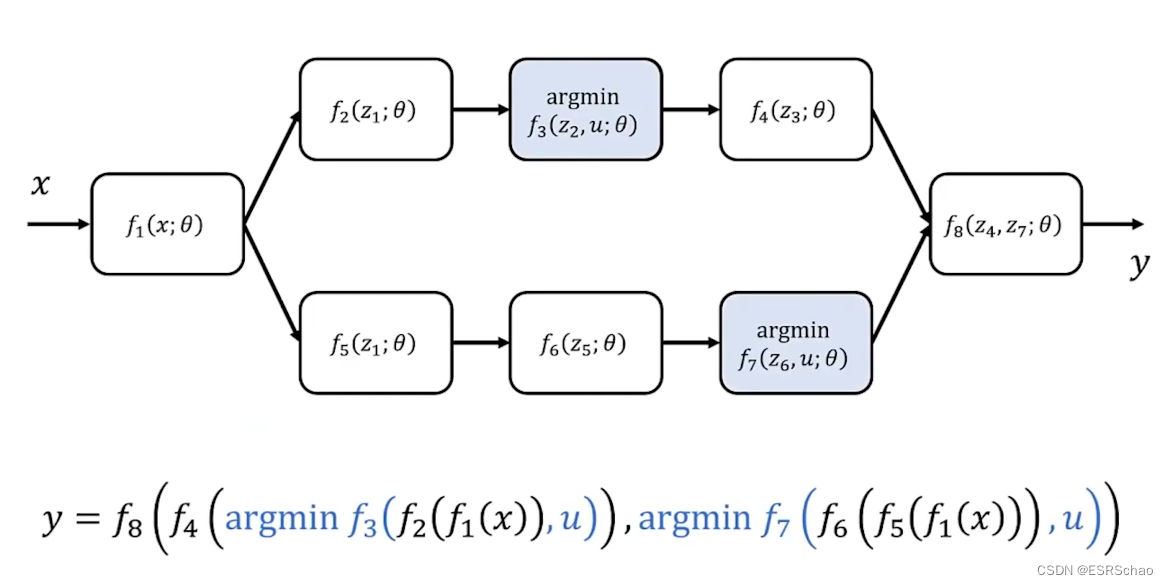
这将网络的输出$y$定义为这些函数的组合，如下式所示：

每个函数都从图中的父节点获取输入， 图中还定义了误差信号（或者叫梯度）的传播方式，从而进行反向传播来更新每个节点的参数$\theta$。
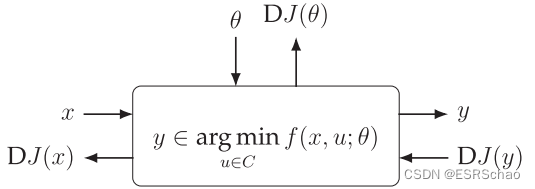
下图展示了一个普通的神经网络进行前向传播和反向传播的过程：

通过链式法则我们可以更新整个网络的参数，这些是神经网络的基础知识，这里不再赘述。
从这个图中我们可以看出一般的神经网络的前向传播和反向传播是解耦的，通过自动微分的计算我们可以轻松的完成每个节点参数的计算更新。

1.2 神经网络举例（第二个关键思想）

这里举例使用的巴比伦算法在实现时并不需要反向传播过程，作者只是在举例说明

以牛顿迭代法（巴比伦算法）的前向传播为例：

我们可以看到在前向传播中$y$在不断的迭代，最后输出结果$y_T$。这个迭代的过程我们可以通过链式法则得到反向传播的梯度公式：

这里给出的公式对x求偏导的部分我感觉不大对，但是不咋影响理解，毕竟只是举个例子。（当然可能我理解有偏差，欢迎讨论）
反向传播部分，因为要求解的结果$y=\sqrt{x}$，将其进行反向传播时有：

进而得到了反向传播部分的函数：

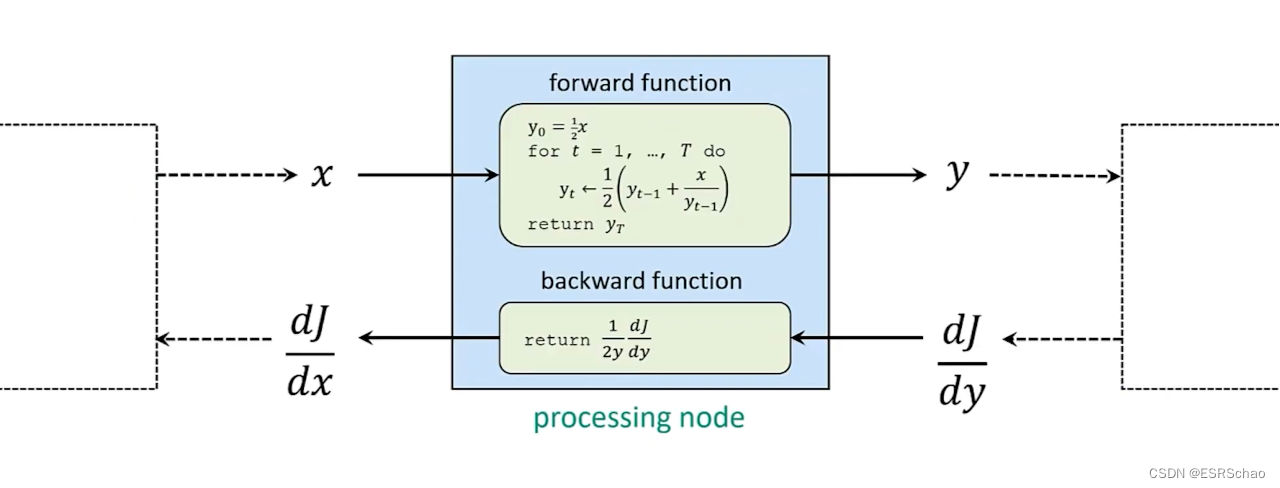
这样我们就得到了整个过程的公式化表达：

注意，这里原视频作者演示的过程并非神经网络，只是在演示这种封闭的前向函数与链式法则等计算方法，供读者学习之后的可微优化问题时加深理解用（它们没有封闭的前向实现）。
总结一下，在平常我们构建神经网络时，我们通常使用自动微分来从前向传递中获得反向传播。这在一般的神经网络中都十分好使，但是要记住一点就是我们有的时候不必使用自动微分 ，通过分离前向传播和后向传递的实现细节进行计算也同样可行。

1.3 深度学习模型中的隐式函数（第三个关键思想）

在我们之前的例子中可以看到神经网络的节点一般都有明确的函数定义，我们通常可以通过数学表达式计算给定输入的输出，这种方法或许很容易就能计算出反向传播时的导数。但是这里我们要研究的时另一种函数——隐式函数：

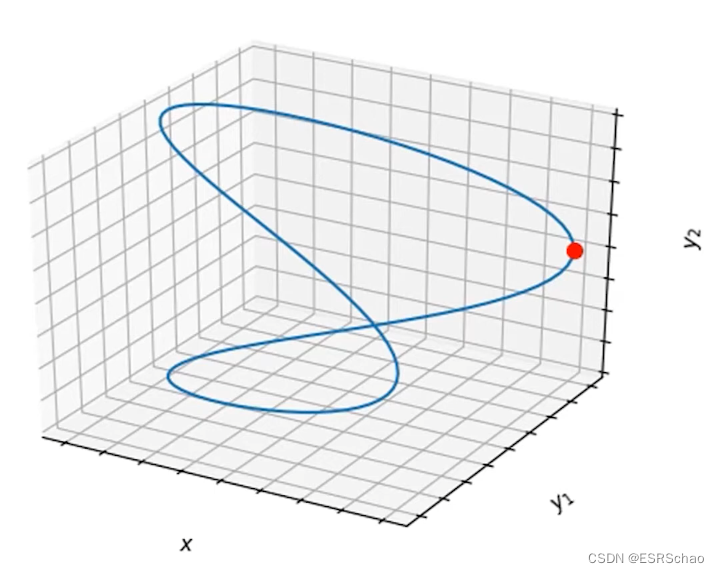
这种函数的输入和输出虽然满足一定的关系，但是输出并非直接作为给定输入的显式函数给出。
作者这里给出的示例函数如上图所示，这里的函数有一个输入变量x和两个输出变量y1和y2。
这里的y和x就可以用一个隐式函数表示：
$$\psi (x,y)=(x-y_1^2+y_2^2{)}^2+(y_1^2+y_2^2-1{)}^2$$
对于式子
$$\psi (x,y)=0$$
我们需要一种能够找到对应y的方法，在教程的后半部分我们将讲解一些隐式函数求解的方法。
现在我们可以写出刚刚这个示例的解空间。

首先我们可以将这个式子看成输入x和输出y的链接（蓝色部分）以及y的约束（黄色部分）的组合。
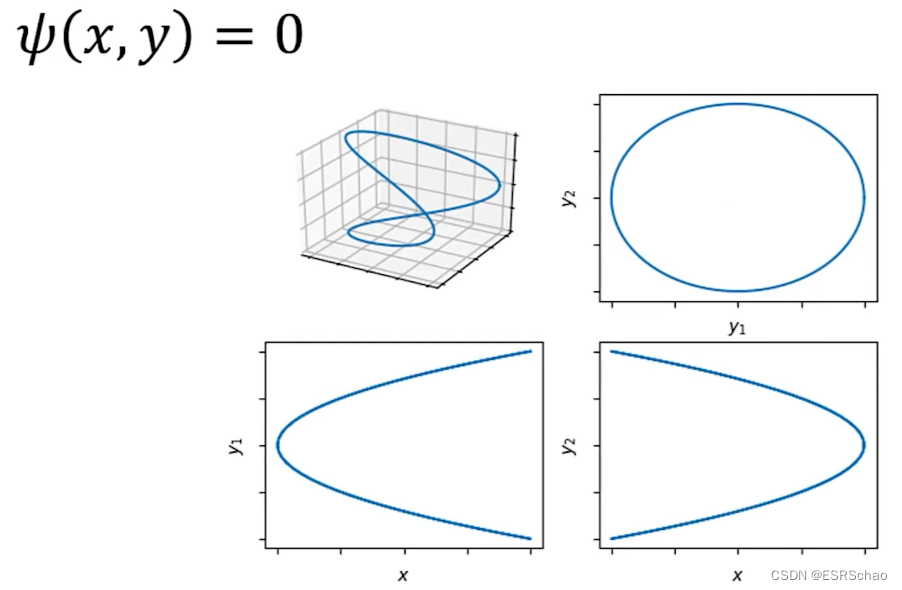
下面这张图展示了这个例子的零水平集：

这张图展示了各个量单独的关系，即使没有显式函数表达，我们依旧可以使用隐函数定理来计算出y相对于x的梯度。对于(-1, 1)范围内的所有x，恰好有四种解，而对于x等于±1的情况有两种解（此时y1或者y2等于0）。
隐函数定理回答了当隐函数$\psi (x,y)=0$时$dy/dx$的值的求法：
通过偏导

我们就可以求得$dy/dx$的值：

这个公式就是隐函数定理，在之后我们会用到。

2. DDN基础知识

正如上部分所讲解的，传统的神经网络架构一般来说都是一些简单的显式函数的组合，现在的研究者在探讨嵌入式可微优化问题的深度学习模型，对于优化问题，我们可以将其转化为前向通道明确定义函数。例如刚刚提到的例子：

对于在约束条件$||y|{|}^2=1$下让y的值最小的优化问题，我们可以将其转换为x在(-1, 1)取值下找到式子$(x-y_1^2+y_2^2{)}^2+(y_1^2+y_2^2-1{)}^2=0$的y的对应的过程。

接下来我们将通过介绍命令式节点和声明式节点来介绍DDN的基础组成。

2.1 DDN的组成

2.1.1 命令式&声明式节点

命令式节点

对于命令式节点，它是一种对于前向通道函数$\tilde{f}$为显式函数的神经网络节点，此时节点的输出为

$$y=\tilde{f}(x;\theta )$$

这里的$x$为输入，$\theta$为节点待学习的参数。

声明式节点

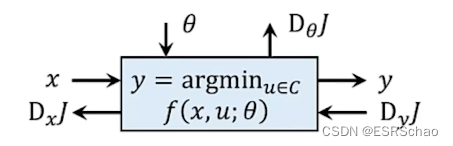
在一个声明式节点中，输入和输出的关系被定义为一个优化问题的解：

这里的$f$是目标函数，$C$是约束。

2.1.2 DDN举例——池化

我们以平均池化举例:
{ x i ∈ R m ∣ i = 1 , . . . , n } → R m \{x_i \in \mathbb{R}^m|i=1,…,n\}\to\mathbb{R}^m {
xi​∈Rm∣i=1,…,n}→Rm
在平均池化的过程中我们需要求解的是输入$x_i$的平均值。
我们可以用两种不同的公式来表述这个问题：
第一种方式——命令式表示

第二种方式——声明式表示

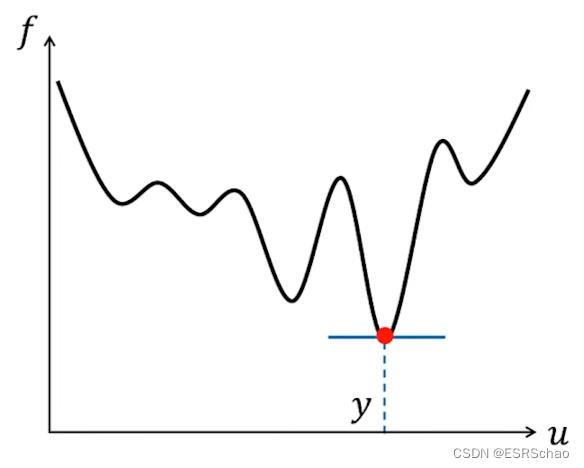
这里的向量$u$和和输入向量$x_i$之间的距离为最小值。

这种方式去考虑平均池化的优点是它允许我们通过最小化鲁棒惩罚来替代l2距离，可以用鲁棒平均值来代替当前平均值。这也说明了有些情况可以强行使用声明式表示，而且所有的命令式节点都可以表示为声明式节点。

声明式节点和命令式节点可以存在于同一个网络中：

那么问题就出现了——假如我们可以去解决前向通道中的优化问题，那么我们要如何求取声明层反向传播的梯度：

这就是深度声明网络中的主要问题了。
我们已经了解了优化问题所需的所有要素，即隐式函数形式的最优条件和隐式函数定理，我们可以写出一个方程，求出特定解相对于输入的导数。对于问题的输入$x\in {\mathbb{R}}^n$我们可以定义它的解集$Y(x):{\mathbb{R}}^n\rightrightarrows {\mathbb{R}}^m$如下式：

Y ( x ) = arg min ⁡   u { f ( x , u ) : h ( x , u ) = 0 p , g ( x , y ) ≤ 0 q } Y(x)=\argmin\ _u\{f(x,u):h(x,u)=0_p,g(x,y)\leq0_q\} Y(x)=argmin u​{
f(x,u):h(x,u)=0p​,g(x,y)≤0q​}

其中$f(x,u)$为目标函数，$h(x,u)=0_p,g(x,y)\le 0_q$为约束条件。

笔者补充
在上述表达式中，$0_p$ 和 $0_q$ 表示的是约束编号，用于区分不同的约束。这些编号用来指明在问题中有多少个等式约束和不等式约束。

然后对于任意的$y\in Y(x)$，有：
$$dy/dx=H^{-1}{A}^T(A{H}^{-1}{A}^T)(A{H}^{-1}B-C)-H^{-1}B$$

这个表达式包含了目标函数和约束函数的部分一阶和二阶偏导。这一结果的证明是将隐函数定理直接应用于 KKT 最佳条件。

2.1.3 证明（无约束条件）

下面给出无约束条件下的定理的证明。假设y是对于无约束变量u的优化问题的解，我们都知道当函数$f$对$y$的导数为0时该解必定出现。
$$y\in argmi{n}_{u}f(x,u)\Rightarrow \frac{\partial f(x,y)}{\partial y}=0$$
我们将其定义为隐式函数$\psi (x,y)\triangleq \frac{\partial f(x,y)}{\partial y}$并应用隐函数定理我们可以得到：
$$\frac{dy}{dx}=-(\frac{{\partial }^{2}f}{\partial y^2}{)}^{-1}\frac{{\partial }^{2}f}{\partial x\partial y}$$
这里的$-(\frac{{\partial }^{2}f}{\partial y^2}{)}^{-1}\frac{{\partial }^{2}f}{\partial x\partial y}$就是之前提到的$-H^{-1}B$。

总结

到这一步我们就知道了一个声明式层需要的是什么了，总结一下：

前向通道

• 一种解决优化问题的方法

反向传播

• 最优化条件(目标函数以及约束)
• (前向通道得到的结果缓存)
• 不需要去知道这个问题是如何解决的，直接计算即可

在接下来的几章我将通过作者提供的官方教程例程来进行具体的讲解，敬请期待。（有些概念作者没弄明白的后面如果开窍了会进行补充，欢迎讨论指正）

今天的文章cnn代码详解_cnn代码详解分享到此就结束了，感谢您的阅读。