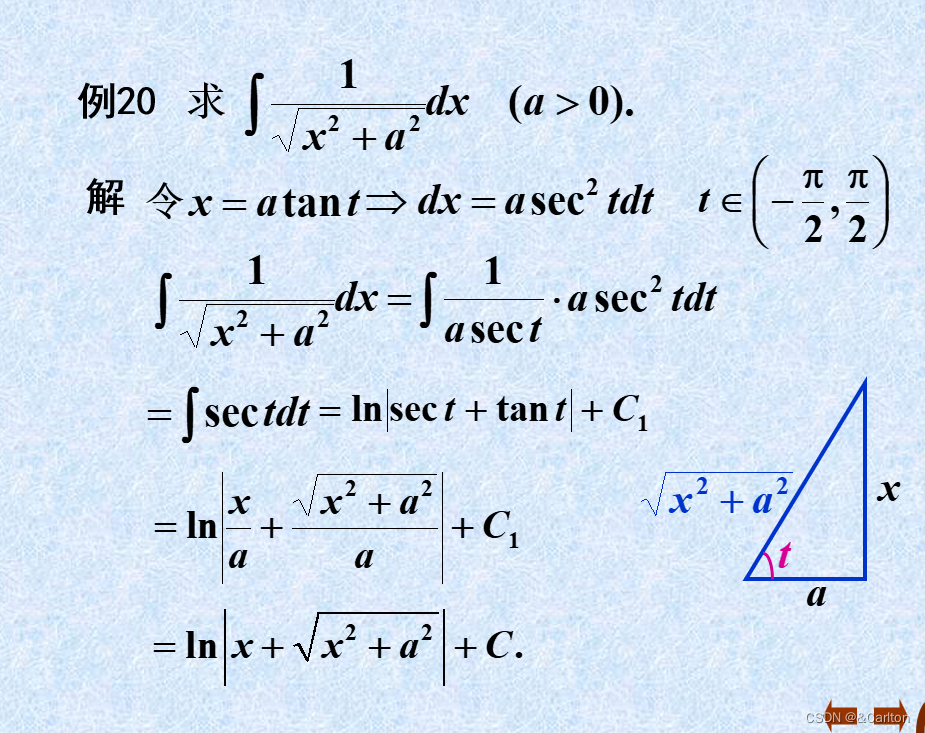第二类换元积分法三角代换_第二类换元积分法t的范围

引例：

        不定积分常用公式证明  ，

例1：

例2：

提出问题：

        为何例1中 t 的范围为（-pi/2，pi/2？例2中 t 的范围为(0.pi/2) 和 (pi,3*pi/2)?

        这么做出于什么原因，有什么目的？

原理：

        ①第二类换元积分法使用条件

                下文均称换元后的函数为 “换元函数”

                换元函数需连续，其导函数恒不等于0（否则说明换元函数为常数a，其反函数为x=a，即此时换元函数的反函数导数不存在）

                总的来说：👉换元函数有可导的反函数

                引例中的各区间满足换元函数单调，x与y是一 一对应的关系，反函数存在，且换元函数导函数连续、不为0，反函数可导。

更多内容：

反函数的导数证明：（看看其前提、条件）

第二类换元积分法证明：（看看其前提、条件）

         ②有效换元的前提:自变量范围不应改变

                有些区间也满足换元函数导函数连续且不为0，但不能完全覆盖原来x的取值范围

                举个栗子：例1  t 只取(0,pi/2)

                                  例2  t 只取(0,pi/2)

        ③换元的目的：简便积分求解

                同时有些区间既满足换元函数有可导的反函数，又满足覆盖原来x的取值范围，但会带来绝对值正负的讨论，如：

                例1中 t 取(0,pi/2)U(pi/2,pi)，(sect)^2开根后带绝对值

                例2中 t 取(0,pi), (tant)^2开根后带绝对值

                基于简便的原则，合理取定取值范围能最便捷地求解积分。

结语：学好数学能摸猫猫

？

        （学数学提高逻辑思维能力与行动力，所以能摸猫猫（x））

今天的文章第二类换元积分法三角代换_第二类换元积分法t的范围分享到此就结束了，感谢您的阅读。