仿射变换基本定理_可视化微分几何和形式

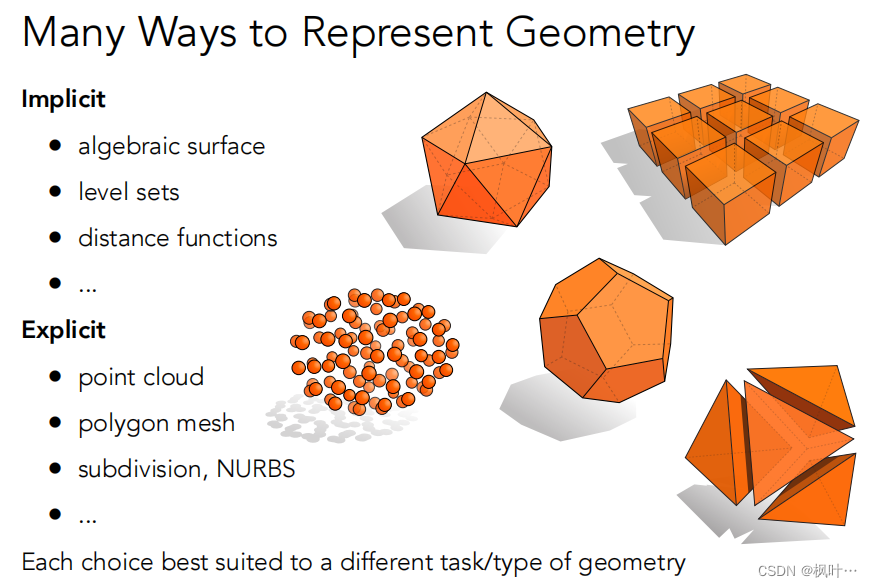
几何的表示方法

分为显式(Explicit)和隐式(Implicit)。

隐式几何的表现形式：

• algebraic surface
• level sets
• distance function
  显式几何的表现形式：
• point cloud
• polygon mesh
• subdivision,NURBS

隐式的几何表示（Implicit）

不会告诉你几何体上的点在哪，而是把几何体上点的关系告诉你。

表达式

基于对点进行归类，找到满足特定关系的点。更通用的表示，f(x,y,z) = 0

优点：

1. 很容易判断点是否在面上。（将点代入f(x,y,z)，正数表示点在图形外，负数表示点在图形内，0表示点在图形上。）
2. 表述起来很容易（对存储很有利）。
3. 容易做面与光线求交。
4. 容易描述和处理拓扑结构。

缺点：

1. 难以描述复杂的形状，
2. 很难知道这个面上有哪些点，很难看出式子表示的是什么形状。

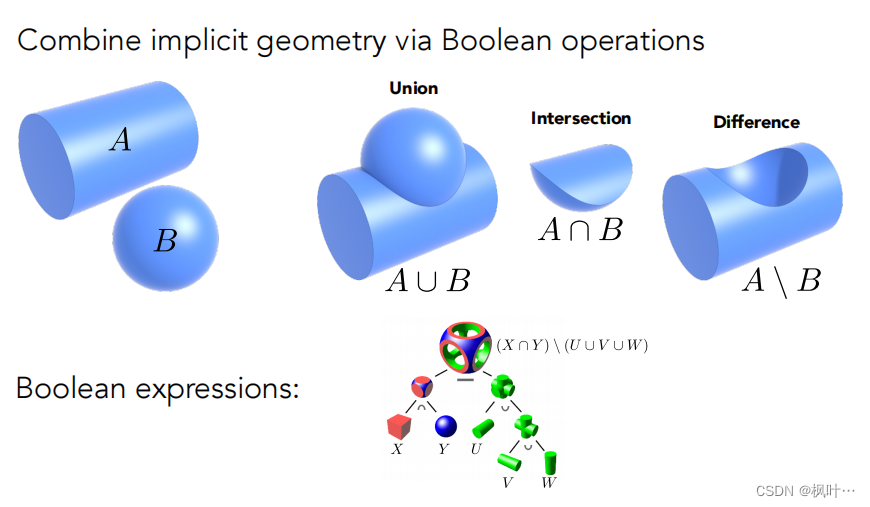
CSG —— Constructive Solid Geometry(Implict)

通过一系列基本几何的基本布尔运算来定义新的几何。

距离函数 Distance Function（Implict）

距离函数：对于任何一个几何，不描述它的表面，而去描述空间中点到各个几何物体表面的最近距离，这个距离可以是正or负（Signed Distance 有向距离），后对于各个几何物体的距离函数进行运算，就可以得到blend融合后的距离函数。

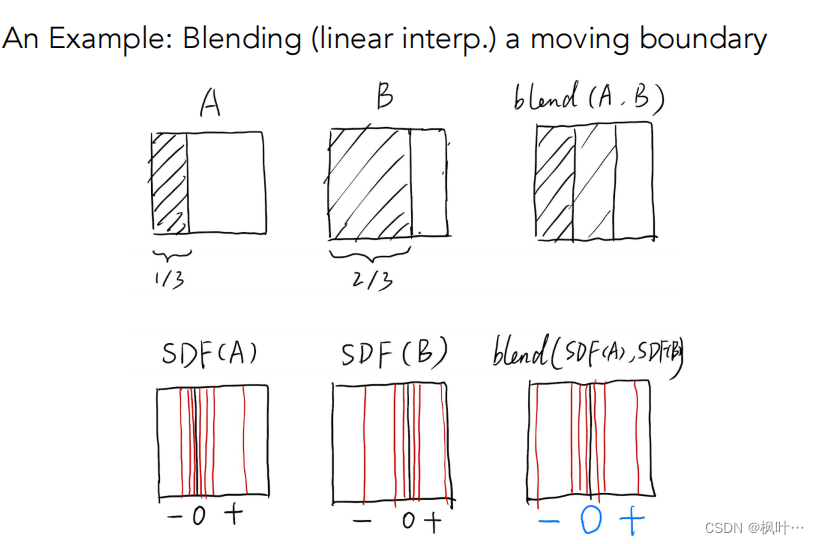
例子：混合一个移动的边界

通过blend两个SDF可以得到移动后的边界。
分别求出两个物体对应的距离函数， 然后把他们blend起来，可以获得由1/3到2/3移动的中间状态，一半白一半黑，边界是SDF=0.

分别计算出圆形和正方形的距离函数，输出的的面为SDF=0

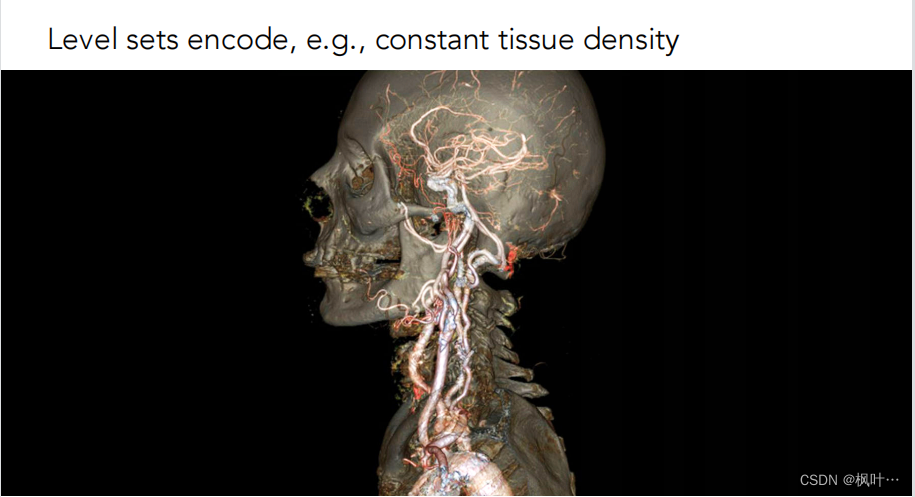
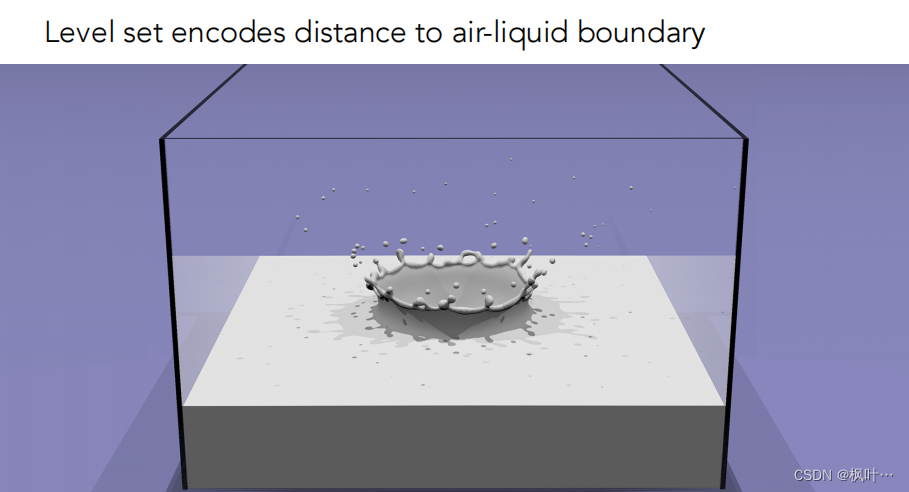
水平集 Level Set Methods(Implict)

封闭形式的方程很难描述复杂的形状，所以选择一种替代方案：存储一个值近似函数的网格（可以是二维的也可以是三维的）
水平集可以理解为SDF的一种特殊状态，即表述方式不一样（SDF对于空间中的点有具体的定义，通过函数表示。而水平集则是对空间进行线性插值（格子）去近似得到一个函数曲线）。水平集通过对于每个点在定义好的格子上进行线性插值，得到每一个格子的具体函数值，找出所有f(x)=0的点的曲线。

通过找到插值为0的位置来找到表面，它具有一个对形状更加显示的控制。
例子：
如果有一个三维的纹理表示人体不同位置的骨密度，可以让密度函数=某个具体的值，然后找到所有满足这个等式的位置，就可以得到一个表面。

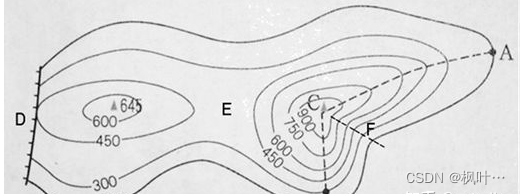
等高线图：

水花 = 空间中所有的水滴融合的结果

分形 Fractals(Implict)

分形又有自相似的意思，自己的部分和整体很像（有点像递归），例子有雪花（不断的六边形）、下面的西兰花等。

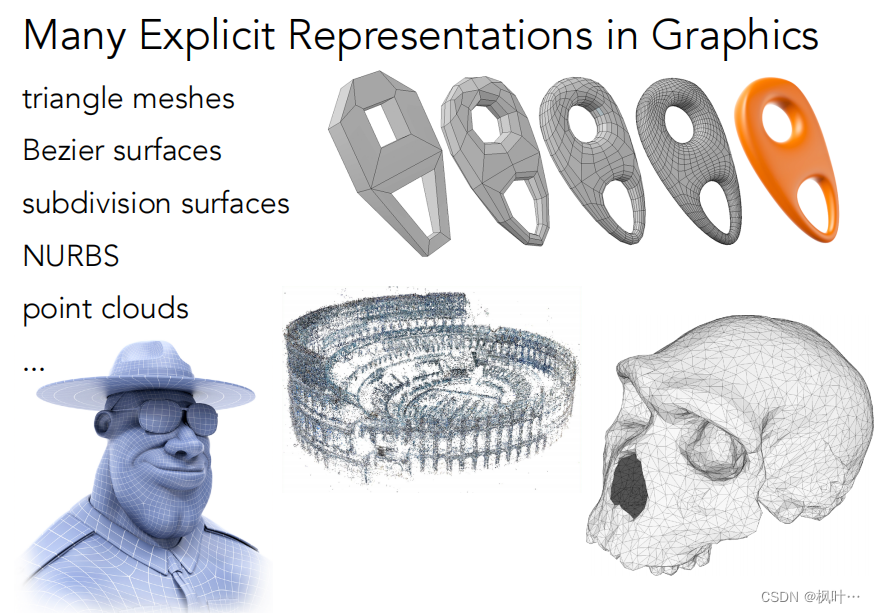
显式的几何（Explicit）

显式几何也有很多种表示方法，例如三角形面、贝塞尔曲面、细分曲面、NURBS、点云等。
优点：对于表示形状很容易。
有点：难以判断点是否在表面上（或内、外）。

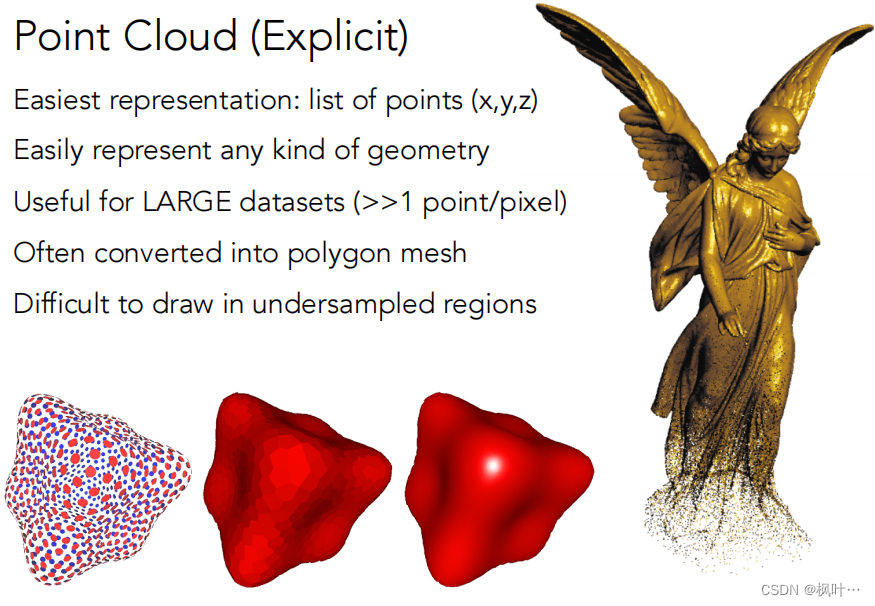
点云（Point Cloud）

• 简单的表示为点的列表(x,y,z)
• 可以简单的表示任何一种几何图形
• 对于表示大数据集是很有用的（>>1 point/pixel）
• 经常被转换成多边形网格
• 难以在采样不足的区域画出来

多边形网格（Polygon Mesh）

• 存储点和多边形（通常是三角形或四边形）
• 容易去处理/模拟，进行自适应采样
• 数据结构比较复杂
• 图形学中最常用的表示

例如obj模型：
把空间中的所有顶点的坐标、法线、纹理坐标等信息记录下来，然后再把它们组合起来（存储在文本中）。
如下图表示了一个立方体

• v是顶点坐标
• vt是纹理坐标
• vn是法线（多了两条是因为建模误差）
• f(face)表示面，比如f 5/1/1 1/2/1 4/3/1 表示这个三角形面是由第5、1、4个顶点组成的，三个点的纹理坐标是第1、2、3对应的纹理坐标，这个面的法线是第一条法线。
  

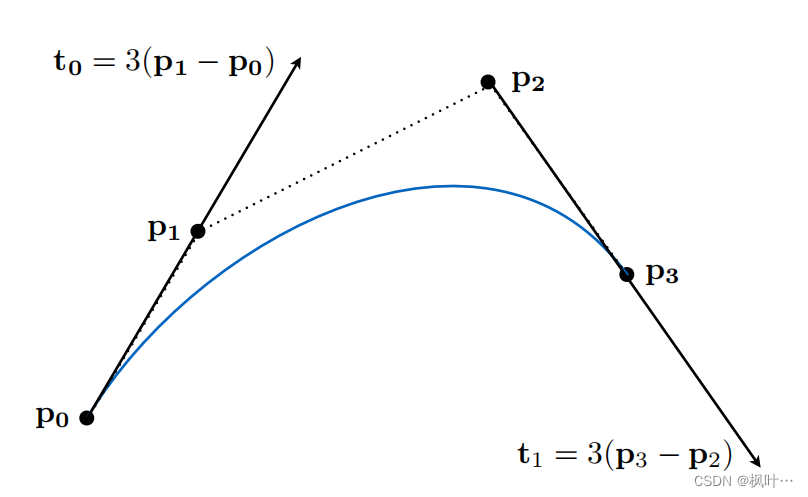
贝塞尔曲线（Bezier Curves）

用一系列的控制点来定义某一条曲线。这些控制点使用切线来定义贝塞尔曲线。

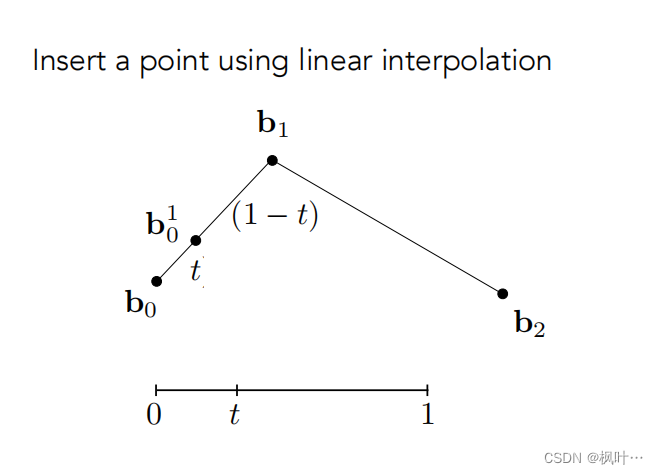
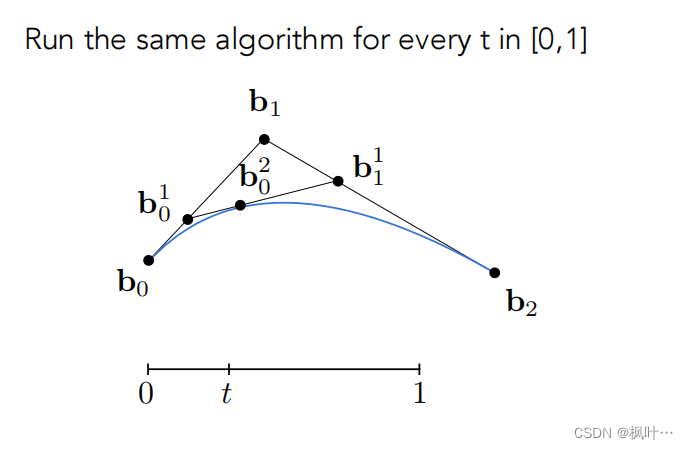
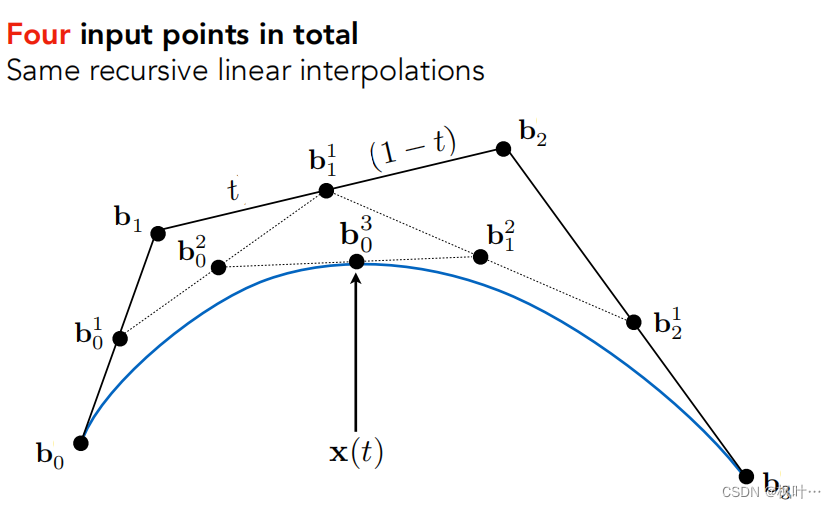
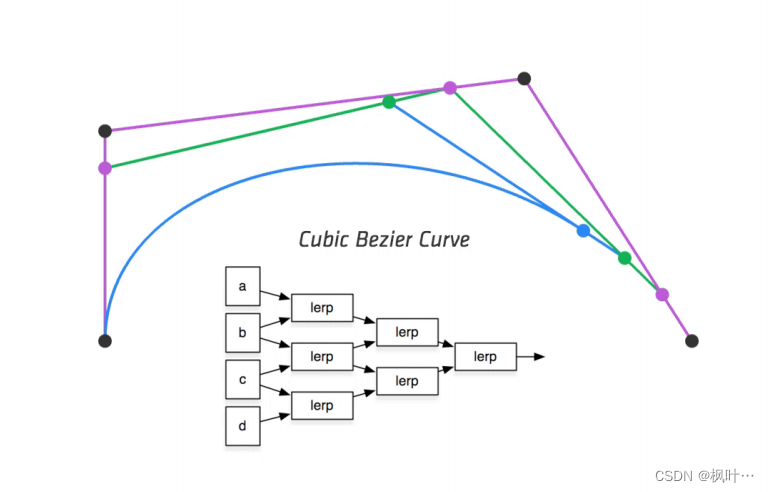
计算贝塞尔曲线——de Casteljau算法

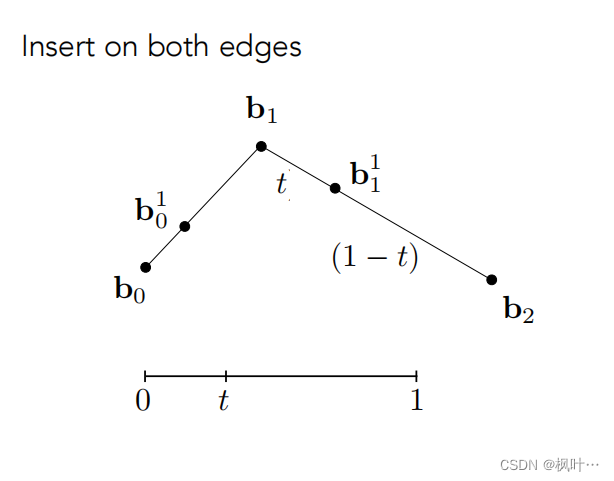
使用线性插值插入点，分别在b₀b₁，b₁b₂以t/1-t的比例插入一个点。


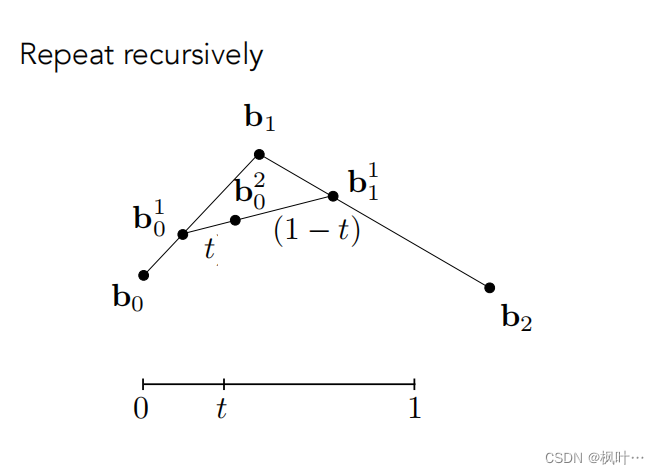
将新得到两个点连接，以相同的方式插入第三个点。

对于[0,1]所有的时间t采用这种算法，最终获得曲线。

多段贝塞尔曲线

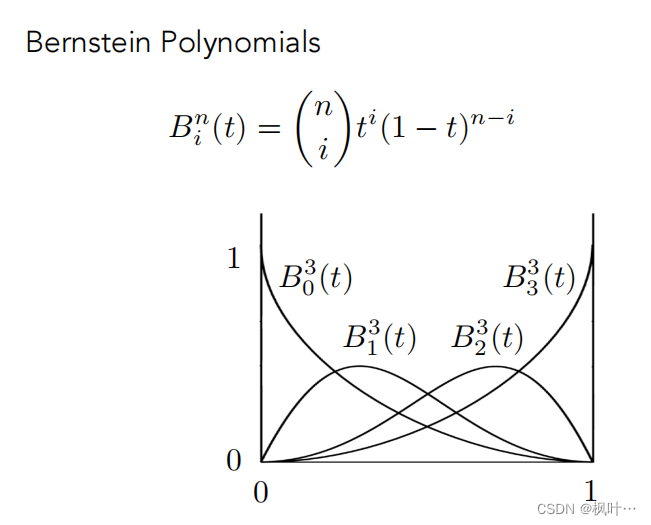
贝塞尔曲线代数公式

如果有n+1个控制点（从0开始编号），可以得到n阶的贝塞尔曲线。


贝塞尔曲线代数实际上是排列组合的公式。

贝塞尔曲线的性质

1. 贝塞尔曲线一定过起点和终点
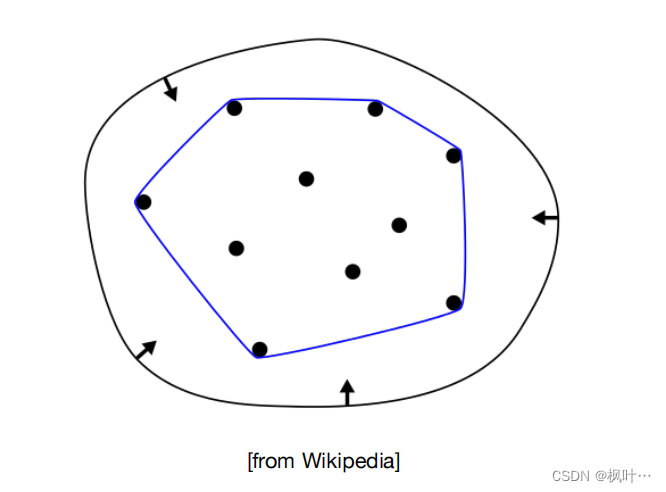
2. 凸包（Convex hull）性质：贝塞尔曲线在控制点的凸包内。
3. 在仿射（Affine）变换下：对贝塞尔曲线做仿射变换与对控制点做仿射变换再获得贝塞尔曲线结果是相同的。
4. 对于3个控制点的贝塞尔曲线，起点和控制点、终点和控制点的连接线都是贝塞尔曲线的切线。

凸包：能够包围几何形体的最小的凸多边形。

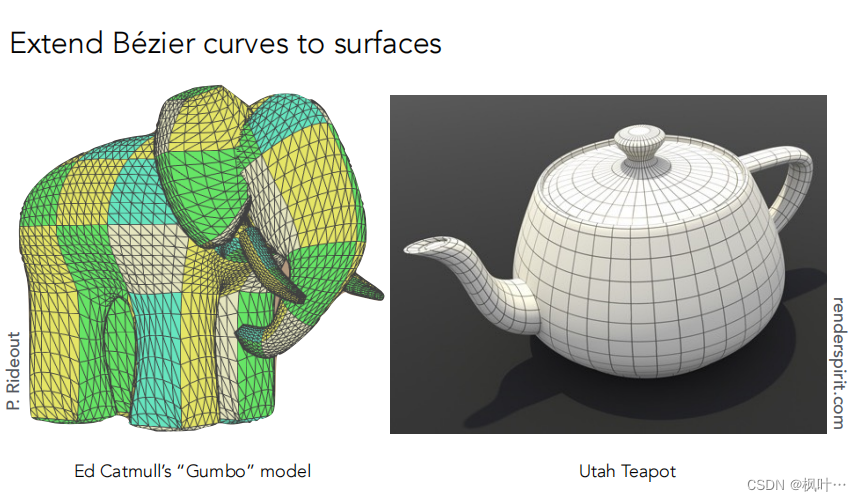
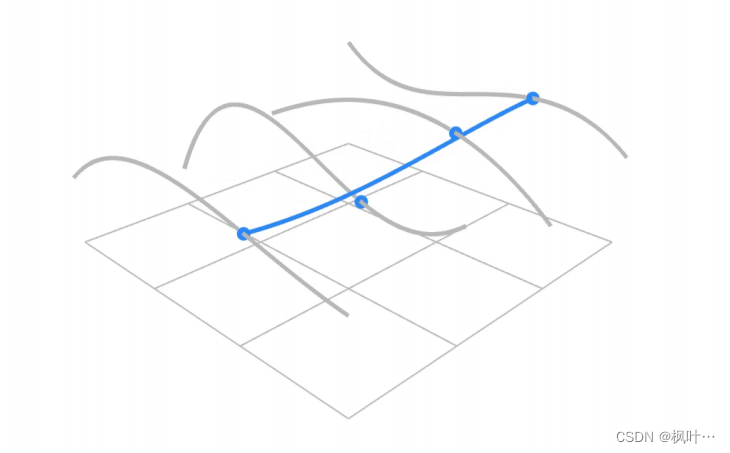
贝塞尔曲面

今天的文章仿射变换基本定理_可视化微分几何和形式分享到此就结束了，感谢您的阅读。