有趣的数学 四元数和八元数简述内容_著名趣味数学游戏

一、四元数简述​

        四元数在代数中，二维复数到三维的推广。四元数及其运算规则是由爱尔兰数学家发明的威廉·罗文·汉密尔顿爵士于 1843 年发明。他将它们设计为描述力学中三维问题的一种方式。经过长期努力设计保留代数正常性质的数学运算，汉密尔顿突然想到了添加第四维的想法。

        这使他能够保留除乘法交换律（一般来说，）之外的正常代数规则，因此四元数仅形成结合 群，特别是非阿贝尔群。四元数是最广为人知和使用的超复数，尽管它们在实践中大部分已被矩阵和向量运算所取代。尽管如此，四元数仍可被视为通过将实数与三维向量组合而形成的四维向量空间，其基（生成向量的集合）由单位向量 1、i 、j和k给出。

        四元数有 4 个维度（每个四元数由 4 个标量组成）、1 个实数维度和 3 个虚数维度。这些虚数维度中的每一个都有一个单位值 -1 的平方根，但它们是相互垂直的不同的 -1 平方根，称为 i、j 和 k。所以四元数可以表示如下：

二、四元数有什么用？

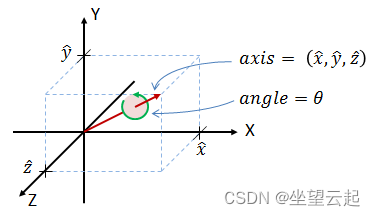
        具体来说，它们对有关绕任意轴的轴角旋转的信息进行编码。旋转和方向四元数在计算机图形学、计算机视觉、机器人学、导航、分子动力学、飞行动力学、卫星轨道力学和晶体结构分析中具有应用。

        有多种方法可以表示计算机图形和其他应用程序的3D旋转。最常见的四种是：欧拉角；四元数；轴角；和旋转矩阵。

        事实上，四元数可以表示 3D 反射、旋转和缩放，但是单个四元数运算不能包含平移，因此如果我们想要围绕原点以外的点旋转、反射或缩放，那么我们必须单独处理平移部分。

        为了计算使用四元数平移点 (Pin) 时的结果点 (Pout)，我们使用以下方程：

        对于反射和缩放：Pout = q * Pin * q

        对于旋转和缩放： Pout = q * Pin * conj(q)

        为什么我们需要 4 个维度来表示 3D 旋转？

        我们可以将 3D 旋转表示为 3 个数字（欧拉角），但这种表示是非线性的并且难以使用。类比是地球的二维地图，我们不可能在不扭曲角度或面积的情况下绘制地球表面的地图。然而，一旦 2D 地图包裹在 3D 球体周围，它就会变成线性的，类似地，当 3D 旋转空间映射到 4D 超球面时，它就会变成线性的。

三、什么是八元数？

        八元数是四元数的超集，就像四元数是复数的超集一样。所以，

• 标量由 1 个数字表示。
• 复数由 2 个数字（1 个实数和 1 个虚数）表示。
• 四元数由 4 个数字表示（1 个实数和 3 个虚数）。
• 八元数由 8 个数字表示（1 个实数和 7 个虚数）。

        我们可能期望这个序列以由 16 个数字组成的元素继续，但是这样的代数不存在，并且该序列以八元数结束。有些代数，例如矩阵和多向量​​，可以具有超过 8 个维度，但它们不具有除法始终存在以及乘法保留范数的相同属性。

        汉密尔顿发现四元数后不久，约翰·格雷夫斯和阿瑟·凯利分别发现了八元数。八元数有时也称为凯莱数。 当我们从复数转向四元数，然后转向八元数时，系统遵循的代数定律更少。当我们从复数到四元数时，我们会失去交换性，而当我们从四元数到八元数时，我们会失去结合性。

        八元数已被用于抽象代数和拓扑等领域，但并没有真正产生很大的影响。1925 年，维格纳和约翰·冯·诺依曼尝试将八元数作为量子力学的基础，但失败了。但是八元数已被用作弦理论的基础，因此八元数可能在描述宇宙结构方面很重要。

四、参考链接

How to Use Quaternions in Industrial Robotics | Mecademic Robotics

Quaternions 

今天的文章有趣的数学 四元数和八元数简述内容_著名趣味数学游戏分享到此就结束了，感谢您的阅读。