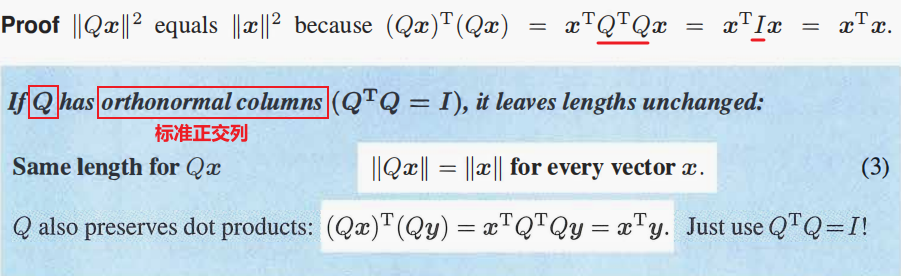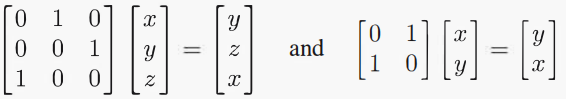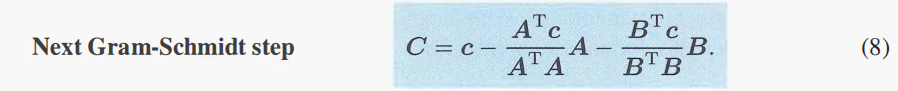标准正交基、施密特正交化
1.标准正交基(Orthonormal)与施密特正交化(Gram-Schmidt)
1.1 标准正交基(Orthonormal)
标准正交基是长度均1的基向量,在子空间中所有标准正交基均互相垂直,即它们的点积为0
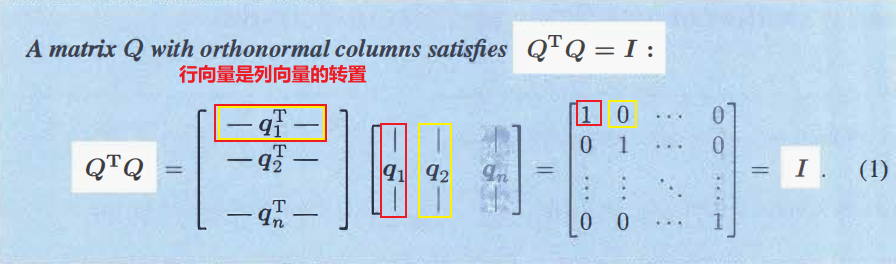
正交矩阵的一个性质:
如果正交矩阵还是一个方阵,则
正交矩阵的性质
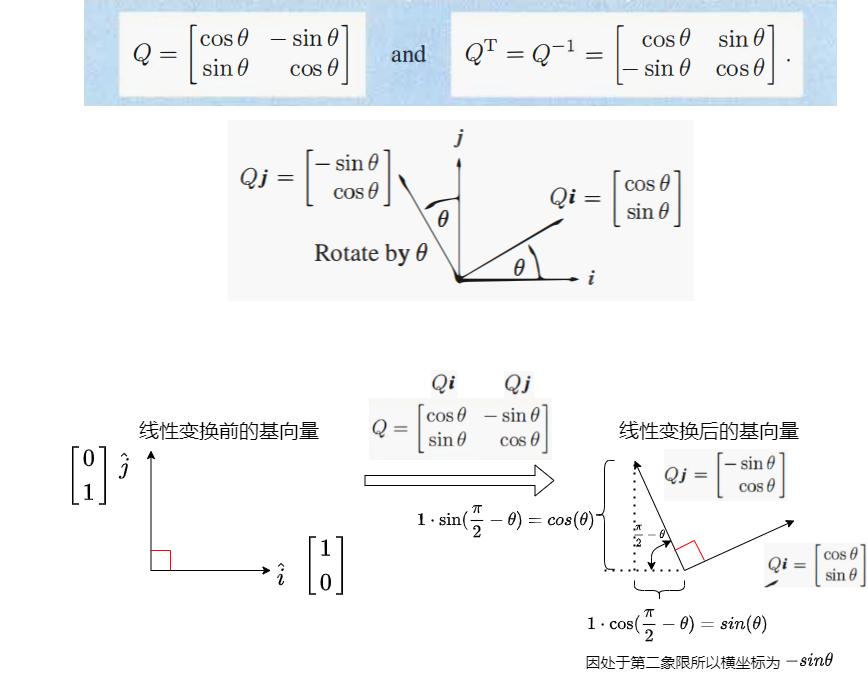
正交矩阵的例子:
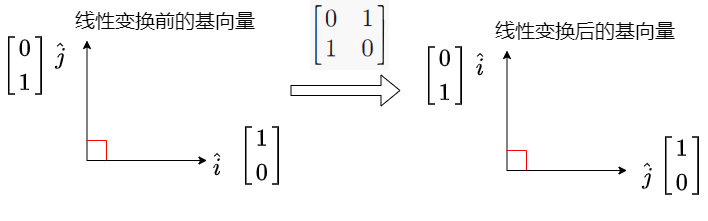
(1)旋转矩阵(Rotation Matrix)
(2)置换矩阵(Permutation Matrix)
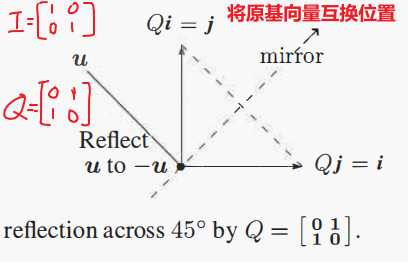
(3)反射矩阵(Reflection Matrix)
注意: u T u \boldsymbol{u}^T\boldsymbol{u} uTu是一个数 、 u u T \boldsymbol{u}\boldsymbol{u}^T uuT是一个矩阵
u T ⋅ u = [ u 1 u 2 ⋯ u n ] ⋅ [ u 1 u 2 ⋮ u n ] = u 1 2 + u 2 2 + ⋅ + u n 2 \boldsymbol{u}^T\cdot\boldsymbol{u}=\begin{bmatrix}u_1\quad u_2\quad \cdots\quad u_n\end{bmatrix}\cdot \begin{bmatrix}u_1\\ u_2\\ \vdots \\ u_n\end{bmatrix}=u_1^2+u_2^2+\cdot+u_n^2 uT⋅u=[u1u2⋯un]⋅⎣⎢⎢⎢⎡u1u2⋮un⎦⎥⎥⎥⎤=u12+u22+⋅+un2
u ⋅ u T = [ u 1 u 2 ⋮ u n ] ⋅ [ u 1 u 2 ⋯ u n ] = [ u 1 u 1 u 1 u 2 ⋯ u 1 u n u 2 u 1 u 2 u 2 ⋯ u 2 u n ⋮ ⋮ ⋱ ⋮ u n u 1 u n u 2 ⋯ u n u n ] \boldsymbol{u}\cdot\boldsymbol{u}^T=\begin{bmatrix}u_1\\ u_2\\ \vdots \\ u_n\end{bmatrix}\cdot \begin{bmatrix}u_1\quad u_2\quad \cdots\quad u_n\end{bmatrix}=\begin{bmatrix}u_1u_1 & u_1u_2 & \cdots & u_1u_n\\ u_2u_1 & u_2u_2&\cdots&u_2u_n\\ \vdots & \vdots & \ddots & \vdots \\ u_nu_1&u_nu_2&\cdots& u_nu_n\end{bmatrix} u⋅uT=⎣⎢⎢⎢⎡u1u2⋮un⎦⎥⎥⎥⎤⋅[u1u2⋯un]=⎣⎢⎢⎢⎡u1u1u2u1⋮unu1u1u2u2u2⋮unu2⋯⋯⋱⋯u1unu2un⋮unun⎦⎥⎥⎥⎤
1.2 施密特正交化(Gram-Schmidt)
Gram-Schmidt 的思路:从每一个新向量中减去它在其他已存在的每个向量的方向上的投影
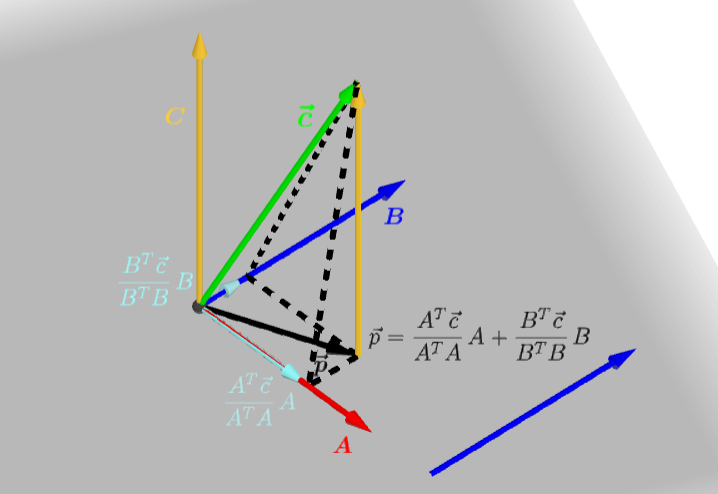
三个线性无关向量 a ⃗ 、 b ⃗ 、 c ⃗ \vec{a}、\vec{b}、\vec{c} a、b、c
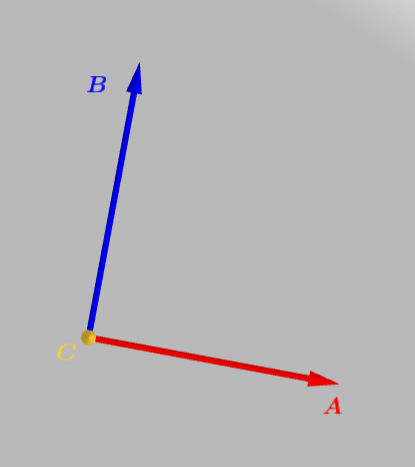
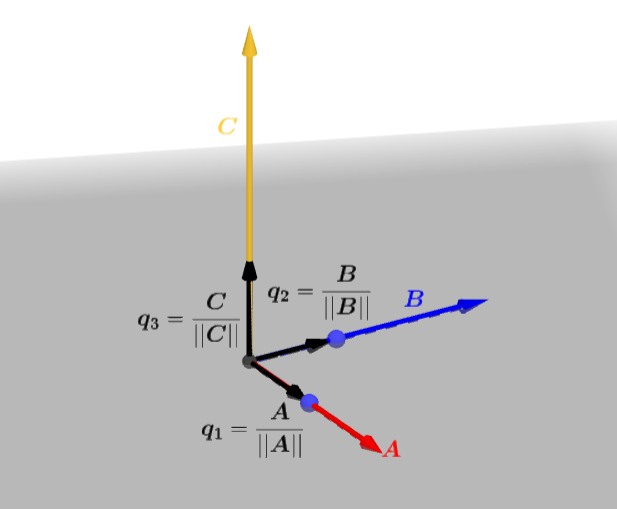
三个正交向量 A 、 B 、 C \boldsymbol{A}、\boldsymbol{B}、\boldsymbol{C} A、B、C
三个标准正交向量 q 1 = A ∣ ∣ A ∣ ∣ 、 q 2 = B ∣ ∣ B ∣ ∣ 、 q 3 = C ∣ ∣ C ∣ ∣ \boldsymbol{q_1}=\frac{\boldsymbol{A}}{||\boldsymbol{A}||}、\boldsymbol{q_2}=\frac{\boldsymbol{B}}{||\boldsymbol{B}||}、\boldsymbol{q_3}=\frac{\boldsymbol{C}}{||\boldsymbol{C}||} q1=∣∣A∣∣A、q2=∣∣B∣∣B、q3=∣∣C∣∣C
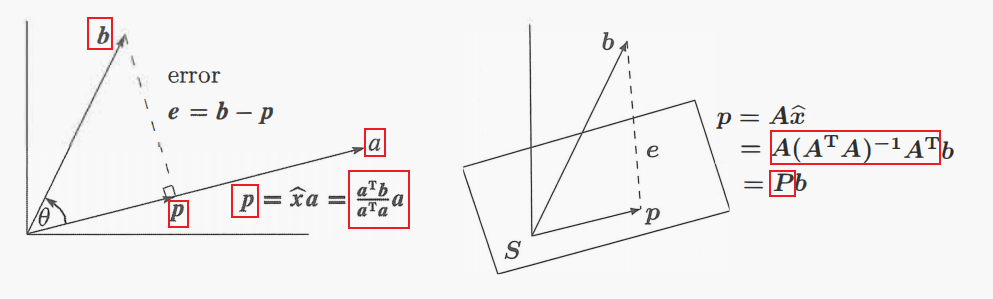
先对投影矩阵 P P P 进行回顾:
施密特正交化第一步:向量 b ⃗ \vec{b} b 与其在向量 a ⃗ \vec{a} a上的投影作差得到与向量 a ⃗ \vec{a} a 正交的向量 B \boldsymbol{B} B,然后我们将向量 a ⃗ \vec{a} a 称作 A \boldsymbol{A} A(注意这里 A \boldsymbol{A} A、 B \boldsymbol{B} B是向量,与未正交化的向量进行区别)
上图中 p ⃗ \vec{p} p 是向量 b ⃗ \vec{b} b 在 向量 a ⃗ \vec{a} a 上的投影向量
A T b ⃗ A T A A \frac{A^T\vec{b}}{A^TA}A ATAATbA 是向量 b ⃗ \vec{b} b 在向量 A \boldsymbol{A} A上的投影向量
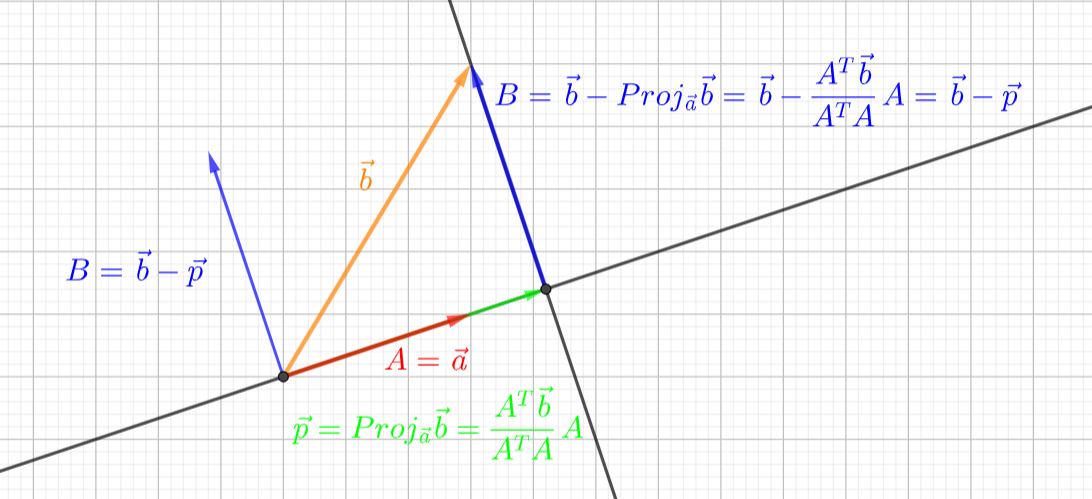
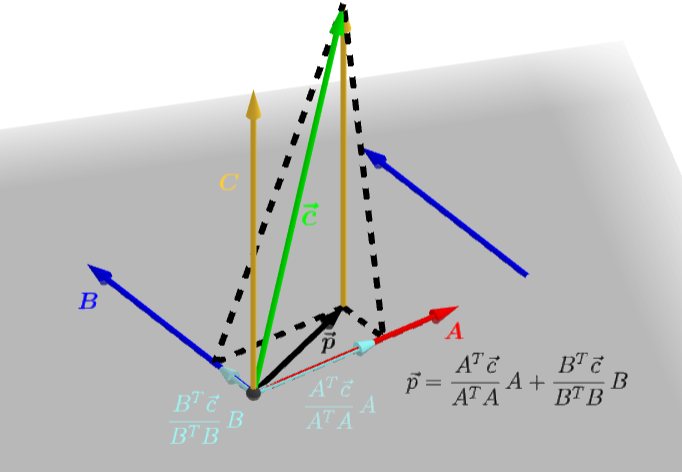
下图中 p ⃗ \vec{p} p 是向量 c ⃗ \vec{c} c 在正交向量 A 、 B \boldsymbol{A}、\boldsymbol{B} A、B 构成平面上的投影向量
A T c ⃗ A T A A \frac{A^T\vec{c}}{A^TA}A ATAATcA 是向量 c ⃗ \vec{c} c 在向量 A \boldsymbol{A} A上的投影向量
B T c ⃗ B T B B \frac{B^T\vec{c}}{B^TB}B BTBBTcB 是向量 c ⃗ \vec{c} c 在向量 B \boldsymbol{B} B上的投影向量
将正交向量单位化
例子:
今天的文章标准正交基(Orthonormal)、施密特正交化(Gram-Schmidt)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/83244.html