柯尔莫哥洛夫统计量_柯尔莫哥洛夫强大数定律

1.检验目标

​ 要实现的一个基本目标是对来自总体的样本$(X_1,X_2,\dots X_n)$，其次序统计量为:$(x_{(1)},x_{(2)},\dots x_{(n)})$。我们估计总体的分布函数为:$F(x)$,问题是如何利用现成的样本$X$依一定的置信概率$1-\alpha$来实现对我们的估计分布函数$F(x)$的检验。

​ 对于连续总体随机变量$X$而言,利用柯尔莫哥洛夫洛夫检验对非正态总体实现拟合优度检验(估计样本的分布函数)要远比卡方分布来的容易，这是因为卡方分布对于连续总体而言要先分组确定各组频率,而这个分组的大小不好确定。而且对于连续总体而言，柯尔莫哥洛夫检验精度要远高于卡方检验。

2.假设检验方法

​ 对于样本来自总体的样本$(X_1,X_2,\dots X_n)$，其次序统计量为:$(x_{(1)},x_{(2)},\dots x_{(n)})$。我们估计总体的分布函数为:$F(x)$,我们可以估计其经验分布函数:
$$F_n(x)=\{\begin{array}{ll}0& x\le x_{(1)}\\ \frac{k}{n}& x_{(k)}<x\le x_{(k+1)}\\ 1& x>x_{(n)}\end{array}$$
​ 由格里文科定理:
P { lim ⁡ n → ∞ sup ⁡ − ∞ < x < ∞ ∣ F n ( x ) − F ( x ) ∣ = 0 } = 1 P\{\lim_{n\rightarrow \infty}\sup_{-\infty <x<\infty}|F_n(x)-F(x)|=0 \}=1 P{
n→∞lim​−∞<x<∞sup​∣Fn​(x)−F(x)∣=0}=1
​ 说明当样本容量足够大的时候,$F_n(x)$是逼近$F(x)$的。

实际上有更进一步的结论(柯尔莫哥洛夫定理):
lim ⁡ n → ∞ P { n sup ⁡ − ∞ < x < ∞ ∣ F n ( x ) − F ( x ) ∣ < y } = K ( y ) = { 0 y ≤ 0 ∑ k = − ∞ ∞ ( − 1 ) k e − 2 k 2 y 2 y > 0 \lim_{n \rightarrow \infty} P\{\sqrt{n}\sup_{-\infty <x<\infty}|F_n(x)-F(x)|<y\}=K(y)=\begin{cases} 0 & y\leq 0\\\sum_{k=-\infty}^{\infty}(-1)^ke^{-2k^2y^2} & y>0\end{cases} n→∞lim​P{
n
​−∞<x<∞sup​∣Fn​(x)−F(x)∣<y}=K(y)={
0∑k=−∞∞​(−1)ke−2k2y2​y≤0y>0​
​ 设$D_n={\sup }_{-\infty <x<\infty }|F_n(x)-F(x)|$,做出如下假设:
$$\begin{gathered} H_0:连续总体分布函数为F(x) \\ {H}_1:连续总体分布函数不是F(x) \end{gathered}$$
​ 当给定置信度为$\alpha$时,分为以下两种情况:

• 当$n\ge 100$时:

  拒绝域$W$为: W = { D n ≥ λ 1 − α n } W=\{D_n \geq \frac{\lambda_{1-\alpha}}{\sqrt{n}}\} W={
  Dn​≥n
  ​λ1−α​​},其中$K({\lambda }_{1-\alpha })=1-\alpha$.

• 当$n<100$时:

  拒绝域$W$为: W = { D n ≥ D n , α } W=\{D_n \geq D_{n,\alpha}\} W={
  Dn​≥Dn,α​},其中$D_{n.\alpha }$查表可得,本次实验就不考虑此种特殊情况。

因此确定好拒绝区域之后,便可以做出如下检验:

​ 若$X\in W$,则接受$H_1$,拒绝$H_0$;反之,若$X\notin W$,则接受$H_0$,拒绝$H_1$。

3.代码实现

话不多说直接附上检验函数(klm_test)代码:

function [error,flag] = klm_test(array,x_list,F_theory,alpha)
%array：Fn(x)区间范围
%F_theory:F(x)
%x_list:采样样本
%alpha:小概率,例如1-95% = 5%
if nargin  < 4
    alpha = 0.05;
end 
x_array = [];fn = [];f = [];
figure(1)
for x = array
   x_array = [x_array,x];
   fn = [fn,Fn(x,x_list)];
   f = [f,F_theory(x)];
end
error = max(abs(f - fn));
plot(x_array,fn,'b.',x_array,f,'r-');
grid on;box on;legend('F_n(x)','F(x)');
xlabel('采样值');ylabel('频率');
Dna = Get_Dna(max(size(x_list)),1-alpha); 
if error < Dna
   flag = 1;
   title(['\alpha=',num2str(alpha),'时的柯尔莫哥洛夫检验通过']);
   disp('柯尔莫哥洛夫检验通过'); 
else
    flag = 0;
    title(['\alpha=',num2str(alpha),'时的柯尔莫哥洛夫检验不通过']);
    disp('柯尔莫哥洛夫检验不通过');
end 
end

function f = Fn(x,x_array)
x_sort = sort(x_array);
x_min = x_sort(1);
x_max = x_sort(end);
n = size(x_array,2);
if x<x_min
    f = 0;
elseif x>= x_max
    f = 1;
else
    f = find(x >= x_sort,1,'last')/n;
end
end

function Dna = Get_Dna(n,alpha)
if n>=100
    k = -1000:1:1000;
    K_x = @(x)sum((-1).^k.*exp(-2*k.^2*x^2));
    x = 0:0.01:2.5;numbers = size(x,2);
    K_xarray = zeros(1,numbers);
    for i = 1:numbers
        K_xarray(i) = K_x(x(i));
    end
    [~,index] = min(abs(K_xarray - alpha));
    Dna = x(index)/sqrt(n);
else
    disp('目前编程只能支持采样点数>100');
    return;
end
end

例如在主函数中当给出以下代码时:

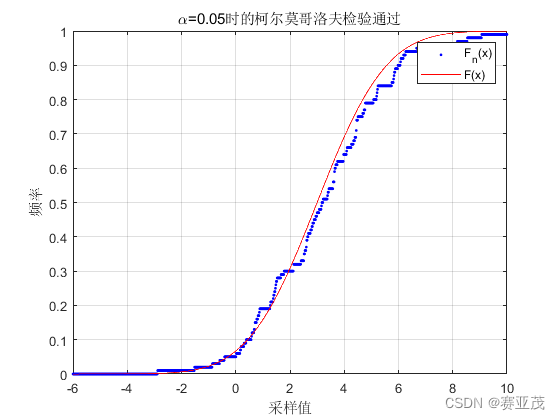
下面代码用来验证正态分布随机数

clc,clear;close all;
rng(0);
x_list = 3 + 2*randn(1,100);
array = linspace(-6,10,1000);
F_theory = @(x)normcdf(x,3,3);
error = klm_test(array,x_list,F_theory);

运行之后会显示:

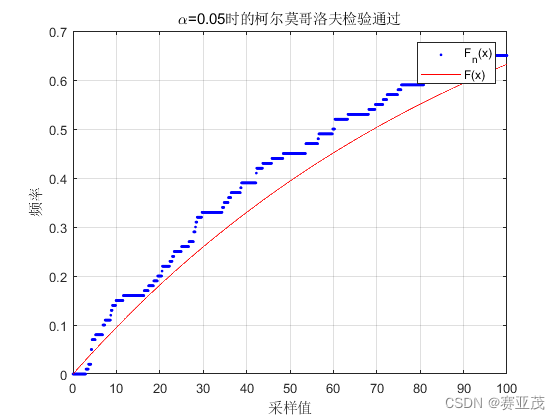
下面代码验证泊松分布合理性

l = 100;
x_list = exprnd(l,[1,100]);
array = linspace(0,l,1000);
F_theory = @(x)(1 - exp(-x/l));
klm_test(array,x_list,F_theory);

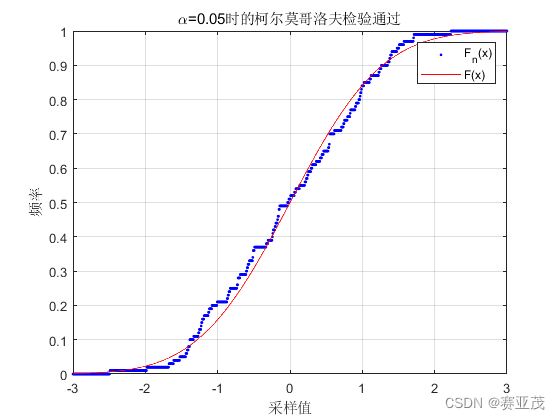
下面验证中心极限定理

numbers = 1000;num = 100;
mu = 1/2;sigma = sqrt(1/12);
x_list = zeros(1,num);
for k = 1:num
    x_list(k) = (mean(rand([1 numbers])) - mu)/(sigma/sqrt(numbers));
end
array = linspace(-3,3,1000);
F_theory = @(x)normcdf(x,0,1);
klm_test(array,x_list,F_theory);

—————2024/03/06更新————————–

事实上，Gilvenko-Cantelli定理描述的是样本个数$n$趋向于无穷时候的偏差分布满足: lim ⁡ n → ∞ P { n sup ⁡ − ∞ < x < ∞ ∣ F ^ n ( x ) − F ( x ) ∣ < y } = K ( y ) = { 0 y ≤ 0 ∑ k = − ∞ ∞ ( − 1 ) k e − 2 k 2 y 2 y > 0 \lim_{n \rightarrow \infty} P\{\sqrt{n}\sup_{-\infty <x<\infty}|\hat{F}_n(x)-F(x)|<y\}=K(y)=\begin{cases} 0 & y\leq 0\\\sum_{k=-\infty}^{\infty}(-1)^ke^{-2k^2y^2} & y>0\end{cases} n→∞lim​P{
n
​−∞<x<∞sup​∣F^n​(x)−F(x)∣<y}=K(y)={
0∑k=−∞∞​(−1)ke−2k2y2​y≤0y>0​而实际情况下，样本个数是有限的，为了保证在有限样本情况下，以一定置信度$1-\alpha$估计样本偏差的合理性，这里需要用到Dvoretzky-Kiefer-Wolfowitz（DKW）不等式，即说明对于任意$\epsilon >0$有：$$\mathbf{P}(\underset{-\infty <x<\infty }{\sup }|{\hat{F}}_n(x)-F(x)|>\epsilon )\le 2\exp (-2n{\epsilon }^2)$$这个不等式是类似于Hoffding不等式的，对上面的不等式进行变形可以得到可以以$1-\alpha$的置信度认为:$$\underset{x}{\sup }|{\hat{F}}_n(x)-F(x)|\le \sqrt{\frac{\log \frac{2}{\alpha }}{2n}}$$事实上上面的不等式右端是相当简单的，它说明了若是想要保证样本的经验分布函数${\hat{F}}_n(x)$和样本的概率分布$F(x)$的上确界足够接近到$\epsilon$,所求的样本个数$n$起码应保证:$$n\ge \frac{\log \frac{2}{\alpha }}{2{\epsilon }^2}$$当$\alpha =0.05,\epsilon =0.01$时，若$n\ge \frac{\log \frac{2}{\alpha }}{2{\epsilon }^2}=18444$可以保证有95%的置信度认为：$$\underset{x}{\sup }|{\hat{F}}_n(x)-F(x)|\le 0.01$$倘若我们想用一个参数为$\theta$的函数$f(x|\theta )$去逼近$F(x)$，则当$n\ge 18444$时，可以以95%的概率认为：$$|f(x|\theta )-F(x)|\le |f(x|\theta )-{\hat{F}}_n(x)|+|{\hat{F}}_n(x)-F(x)|\le |f(x|\theta )-{\hat{F}}_n(x)|+0.01$$因此，要使得$f(x|\theta )$充分逼近$F(x)$，就需要使得$|f(x|\theta )-{\hat{F}}_n(x)|$充分小。

今天的文章柯尔莫哥洛夫统计量_柯尔莫哥洛夫强大数定律分享到此就结束了，感谢您的阅读。