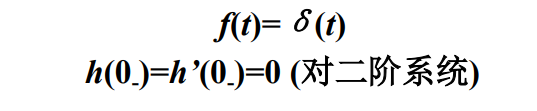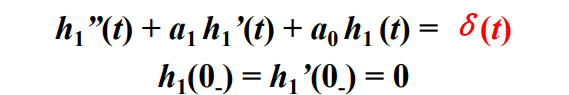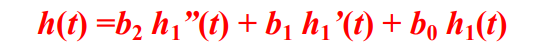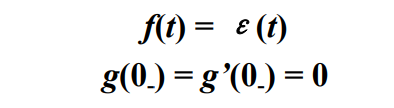什么是信号_随时间连续变化的信号「建议收藏」

冲激响应与阶跃响应

1 冲激响应的定义和求法

定义
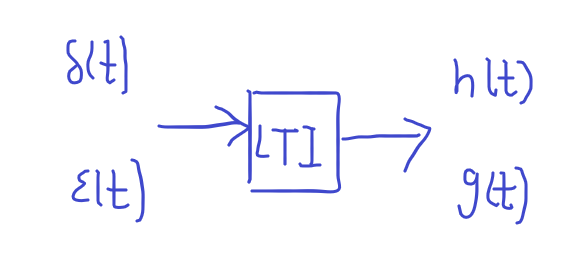
冲激响应是由单位冲激函数$\delta (t)$所引起的零状态响应，记为$h(t)$。

$h(t)$隐含的条件：

基本信号：冲激函数$\delta (t)$
基本响应：冲激响应$h(t)$

求法

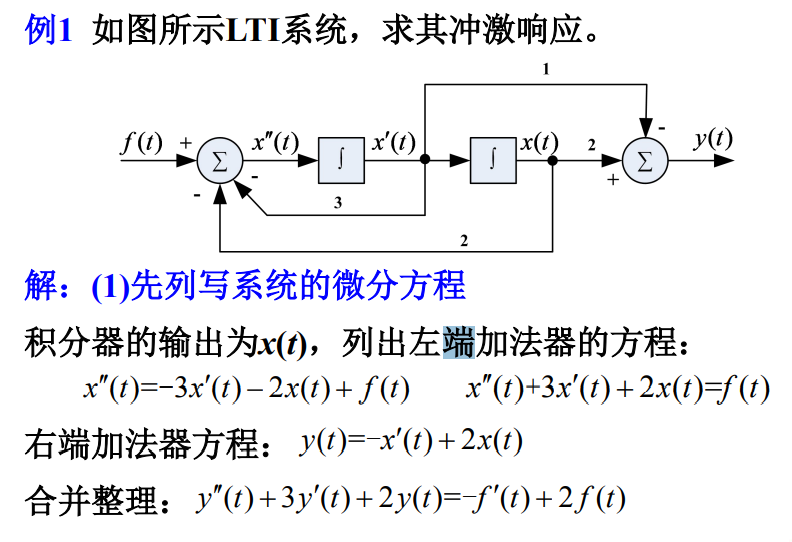
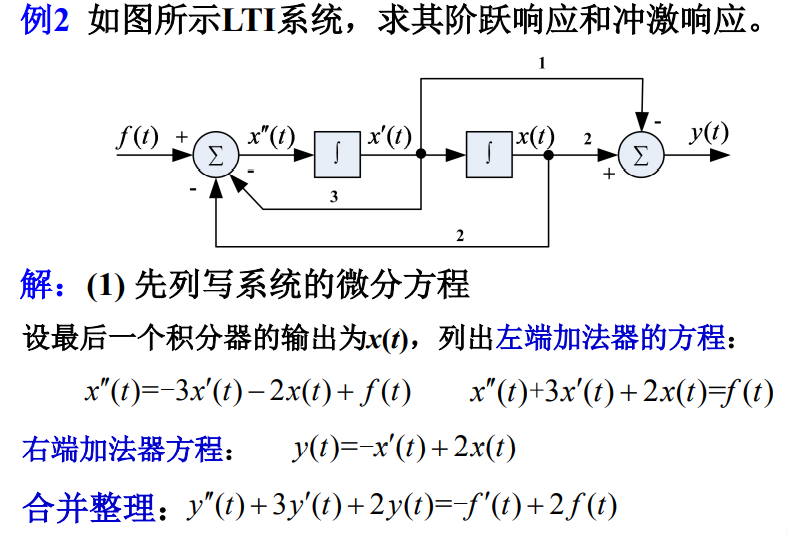
描述二阶LTI系统的微分方程的一般形式为：$$y”(t)+a_{1}y’(t)+a_{0}y(t)=b_{2}f”(t)+b_{1}f’(t)+b_{0}f(t)$$
求解系统的冲激响应 可分两步进行：
(1)选新变量$h_1(t)$，使它满足

采用经典法求解$h_1(t)$
(2)根据LTI系统零状态响应的线性性质和微分特性，则冲激响应：

$t>0$时方程式右边为0，因此特解也应为0.

说明：结合零状态响应的线性性质和微分性质，来简化求解过程；若直接进行求解，方程右端将会出现冲激函数的各阶导数。

$t\ge 0$与$\epsilon (t)$区别：
$t\ge 0$没有告诉你$t<0$是多少；而$\epsilon (t)$则告诉你$t<0$是值为0

2 阶跃响应的定义和求法

定义
阶跃响应是由单位阶跃函数$\epsilon (t)$所引起的零状态响应，记为$g(t)$。

$g(t)$隐含的条件：

基本信号：阶跃函数$\epsilon (t)$
基本响应：阶跃响应$g(t)$

求法

2p=1,特解p为0.5

《工程信号与系统》作者：郭宝龙等
国家精品课程：信号与系统 ，中国大学MOOC，郭宝龙，朱娟娟

今天的文章什么是信号_随时间连续变化的信号「建议收藏」分享到此就结束了，感谢您的阅读。