快速求奇素数的所有原根怎么求_最小的素数是1还是2「建议收藏」

转载自：ACdreamers神博客(请戳这里)

定理：如果p为素数，那么素数p一定存在原根，并且p的原根的个数为phi(p-1).

设m是正整数，a是整数，若a模m的阶等于φ(m)，则称a为模m的一个原根.

假设一个数g对于P来说是原根，那么g^i mod P的结果两两不同,且有 1<g<P, 0<i<P,那么g可以称为是P的一个原根,归根到底就是g^(P-1) = 1 (mod P)当且

仅当指数为P-1的时候成立.(这里P是素数).

求原根目前的做法只能是从2开始枚举，然后暴力判断g^(P-1) = 1 (mod P)是否当且当指数为P-1的时候成立。而由于原根一般都不大，所以可以暴力得到.

求一个奇素数的所有原根方法。

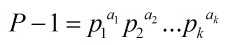
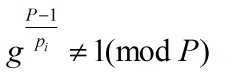
设g是P的平方非剩余，是P-1的标准分解式，若恒有成立，

则g就是P的原根。

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>

using namespace std;

#define LL long long

const int N = 1000010;

bool prime[N];
LL p[N];
LL pr[N];
LL k=0,c;

void isprime()
{
    LL i,j;
    memset(prime,true,sizeof(prime));
    for(i=2;i<N;i++)
    {
        if(prime[i])
        {
            p[k++]=i;
            for(j=i+i;j<N;j+=i)
            {
                prime[j]=false;
            }
        }
    }
}

void cal(LL n)
{
    LL t=n,i,a;c=0;
    for(i=0;p[i]*p[i]<=n;i++)
    {
        if(n%p[i]==0)
        {
            pr[c]=p[i];
            while(n%p[i]==0) n/=p[i];
            c++;
        }
    }
    if(n>1)
    {
        pr[c]=n;
        c++;
    }
}

LL quick_mod(LL a,LL b,LL m)
{
    LL ans=1;
    a%=m;
    while(b)
    {
        if(b&1)
        {
            ans=ans*a%m;
            b--;
        }
        b>>=1;
        a=a*a%m;
    }
    return ans;
}

int main()
{
    LL P,i,t,g,root;
    isprime();
    while(cin>>P)
    {
        cal(P-1);
        for(g=2;g<P;g++)
        {
            bool flag=true;
            for(i=0;i<c;i++)
            {
                t=(P-1)/pr[i];
                if(quick_mod(g,t,P)==1)
                {
                   flag=false;
                   break;
                }
            }
            if(flag)
            {
                root=g;
                cout<<root<<endl;
            }
        }
    }
    return 0;
}

今天的文章快速求奇素数的所有原根怎么求_最小的素数是1还是2「建议收藏」分享到此就结束了，感谢您的阅读。