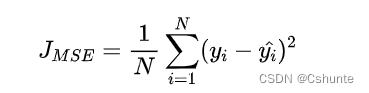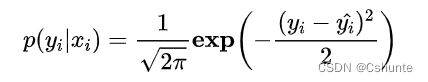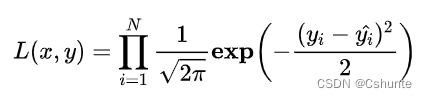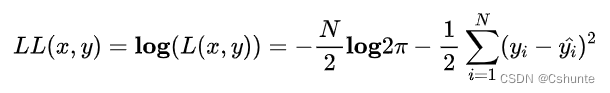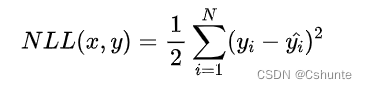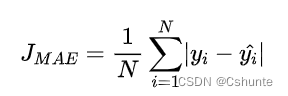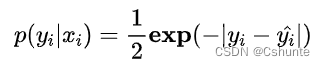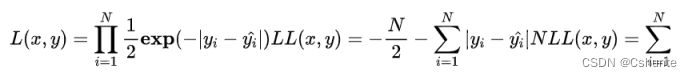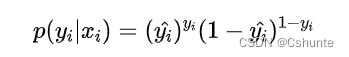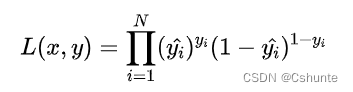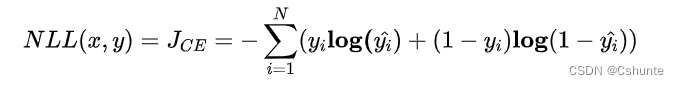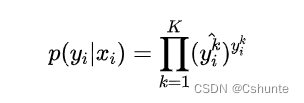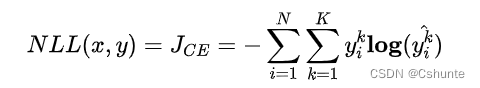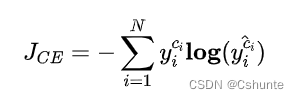交叉熵损失函数计算_meta分析合并效应量

在介绍均方误差损失、平均绝对误差损失、交叉熵损失之前，有必要了解一些术语：

损失函数Loss Funtion：通常是针对单个训练样本而言，给定一个模型输出值和真实值，损失函数输出一个实值损失L = f(yi，y_hat)
代价函数Cost Function：通常是针对整个训练集的总损失
目标函数Objective Function：更通用的术语，表示任意希望被优化的函数，用于机器学习领域和非机器学习领域（如运筹优化等）

一句话总结三者的关系就是： A loss function is a part of a cost function which is a type of an objective function.

①均方差损失 Mean Squared Error Loss

均方差损失是机器学习、深度学习回归任务中最常用的一种损失函数，也称为L2 loss。

原理：

实际上在一般的假设下我们可以使用最大化似然得到均方差损失的形式。假设模型预测与真实值之间的误差服从标准高斯分布（μ=0，σ = 1），则给定一个xi模型输出真实值yi的概率为：

进一步我们假设数据集中N个样本点之间相互独立，则给定所有x输出所有真实值y的概率，即似然Likelihood，为累乘的结果：

通常为了计算方便，可以最大化对数似然Log-Likelihood：

问题可以转化为最小化负对数似然Negative Log-Likelihood：

可以看到这个实际上就是均方差损失的形式。也就是说在模型输出与真实值的误差服从高斯分布的假设下，最小化均方差损失函数与极大似然估计本质上是一样的。

因此这个假设能被满足的场景中（例如回归），MSEL是一个很好的损失函数选择；当这个假设没能被满足的场景中（例如分类），均方差损失则不是一个好的选择。

②平均绝对误差损失：Mean Absolute Error Loss

平均绝对误差MAEL是另一类常用的损失函数，也称为L1 Loss，其形式如下：

原理：

假设模型预测与真实值之间的误差服从拉普拉斯分布Laplace distribution(μ= 0，b = 1)，则给定一个xi模型输出真实值yi的概率为

与上面推导MSE时类似，我们可以得到的负对数似然实际上就是MAE损失的形式

MAE与MSE区别：

MAE与MSE作为损失函数的主要区别是：MSE损失相比MAE通常可以更快地收敛，但MAE损失对于outlier更加健壮，即更加不易受到outlier影响。（outlier代表异常值）

MSE通常比MAE可以更快的收敛。当使用梯度下降算法时,MSE损失的梯度是-yi_hat，而MAE损失的梯度为±1，即MSE梯度的scale会随误差大小变化，而MAE的梯度的scale则一直保持1，即便在预测值与真实值非常相近的时候MAE的梯度scale也同样是1，这实际上是非常不利于模型的训练的。虽然可以在训练过程中动态调整学习率缓解这个问题，但是总的来说损失函数梯度之间的差异导致了MSE在大部分时候比MAE收敛的更快。这也是MSE更为流行的原因。

MAE对于outlier更加robust：

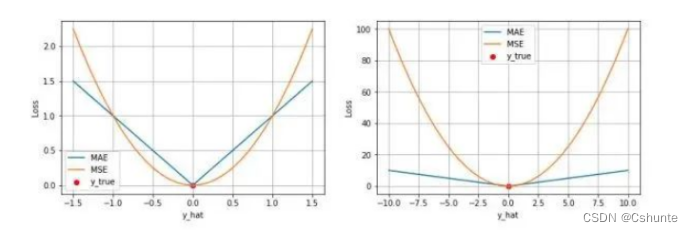
①由于MAE损失与绝对误差之间是线性关系，MSE损失与误差是平方关系，当误差非常大时，MSE损失会远远大于MAE损失。因此当数据中出现一个误差非常大的outlier时，MSE会产生一个非常大的损失，对模型的训练会产生较大的影响。

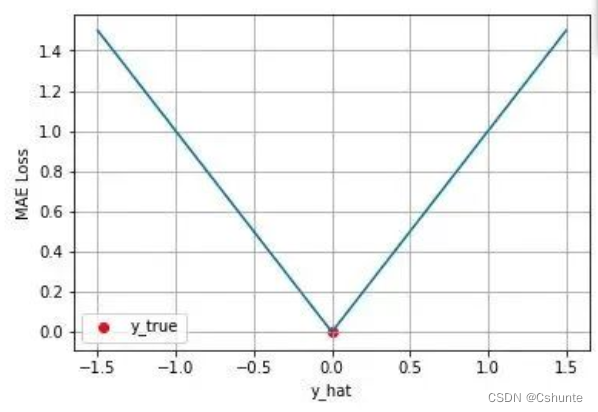
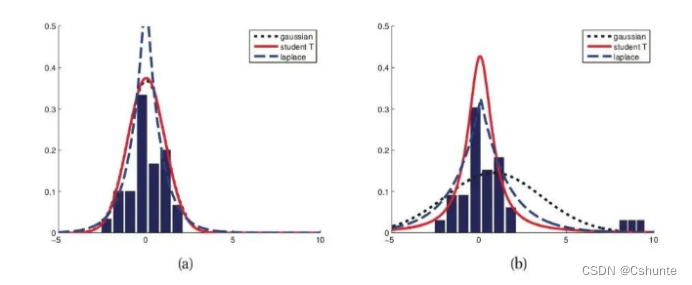
②从两个损失函数的假设出发，MSE 假设了误差服从高斯分布，MAE 假设了误差服从拉普拉斯分布。拉普拉斯分布本身对于 outlier 更加 robust。当右图右侧出现了 outliers 时，拉普拉斯分布相比高斯分布受到的影响要小很多。

③交叉熵损失Cross Entropy Loss

上面介绍的MSE损失和MAE损失都是适用于回归问题的损失函数。对于分类问题，最常用的损失函数是交叉熵损失函数。

二分类：

考虑二分类，在而分类中我们通常使用Sigmoid函数将模型的输出压缩到（0， 1）区间内，y_hat∈（0， 1），用来代表给定输入xi，模型判断为正类的概率。由于只有正负两类，因此同时也得到了负类的概率。于是可以用一条式子来表示两类发生的概率：

假设数据点之间独立同分布，则似然可以表示为

对似然取对数，然后加负号变成最小化负对数似然，即为交叉熵损失函数的形式

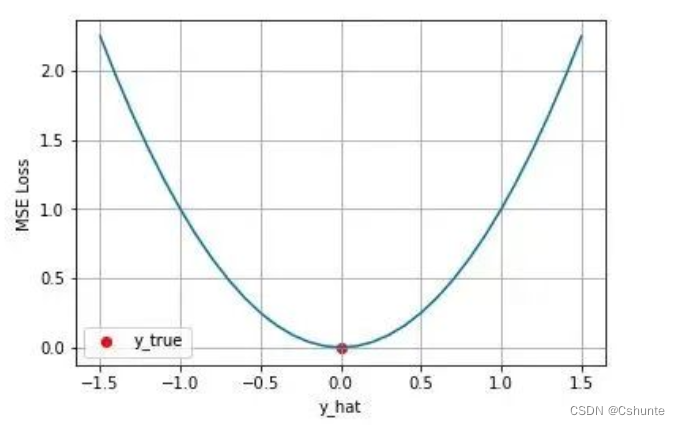
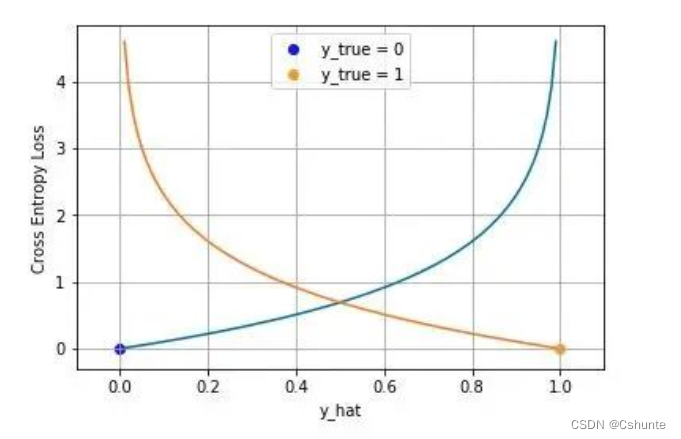
下图是对二分类的交叉熵损失函数的可视化，蓝线是目标值为0时输出不同输出的损失，黄线是目标值为1时的损失。可以看到越接近目标值损失越小，随着误差变大，损失呈指数增长。

多分类：

在多分类的任务中，交叉熵损失函数的推导思路和二分类是一样的，变化的地方是真实值yi现在是一个one-hot向量，同时模型输出的压缩由原来的Sigmoid函数换成Softmax函数。Softmax函数将每个维度的输出范围都限定在（0， 1）之间，同时所有维度的输出和为1，用于表示一个概率分布。