4.1 优化问题
- 基本术语
- 问题的标准表示
- 等价问题
- 参数与谕示问题描述
4.1.1 基本术语




如果
在实际生活中可以这样理解该优化问题,即我们要生产产品,其数量为x,要确定生产数量以使得利润最高,而约束函数则可以理解为在实际产生中受到的限制比如资源消耗等。
问题的定义域:
可行点:
可行集:所以有可行点的集合。
当问题的可行集非空时,我们称为问题是可行的,否则称为不可行。
问题的最优值记为
如果问题不可行,记
如果存在可行解

最优点和局部最优点
如果


如果存在
即,x是关于z的优化问题的解:
全局最优一定是局部最优,局部最优不一定是全局最优。
例子:




min VS minimize
minimize不是min。min是一个取最小值的函数,比如min{0,-1,2}=-1。minimize是优化问题中的一部分,不是对一组数中取出最小值,而是针对一个目标函数,找到使目标函数最小的点。
可行性问题
如果目标函数恒等于零,那么其最优解要么是零(如果可行集非空),要么是∞(如果可行集是空集)。我们称其为可行性问题,有些时候将其写作:
因此,可行性问题可以用来判断约束是否一致,如是,则找到一个满足它们的点。
可以用它来找到函数的定义域(另外还要加上目标函数的隐式约束)。
4.1.2 问题的标准表示
为极小化问题的标准表示形式。
如果是极大问题,即:
极大化问题变极小化问题只需对目标函数取相反数即可得到。
可以将目标函数理解为效用函数。
4.1.3 等价问题
如果从一个问题的解,很容易就能得到另一个问题的解,反之亦然,则称两个问题是等价的。
产生等价问题的变换包括:变量变换、目标函数与约束函数变换、松弛变量、消除等式约束、消除线性等式约束、引入等式约束、优化部分变量、上境图问题形式、隐式与显示约束。
变量变换


那么问题变为:
目标函数与约束函数变换







那么问题变为:
松弛变量

那么问题变为:
消除等式约束
利用参数




消除线性等式约束
如果等式约束均是线性的,即









将
它与原问题等价,不含有等式约束并且减少了rankA个变量。
引入等式约束
考虑这样的问题:
其中


优化部分变量
我们总有:

因此,问题:
等价于:
其中:
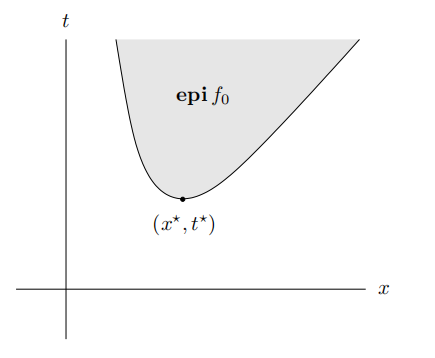
上镜图问题形式
无约束问题的上境图形式问题的几何解释。其目标是寻找上境图中(阴影所示)极小化t的一点,即上境图中最“低”的一点,最优点是(x*,t*)。
隐式和显式约束
上面谈到的不等式约束与等式约束被称为显式约束,他们及目标函数的定义域被称为隐式约束。
4.1.4 参数与谕示问题描述
参数问题描述:对于一个问题为确定目标函数,我们给出函数的系数。即待解决的特定问题被出现在目标和约束函数中的函数参数确定。
谕示问题描述:无法显式地知道f,但对于每个在f的定义域内的x,可以计算得到f(x)。
参考:凸优化第四章凸优化问题 4.1 优化问题
今天的文章凸优化问题的定义_如何证明一个问题是凸优化问题分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/84639.html