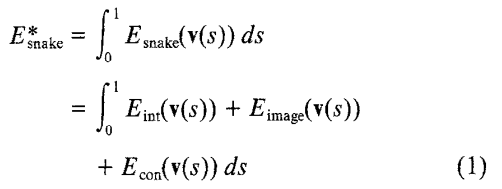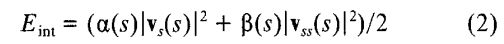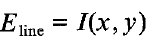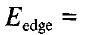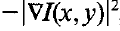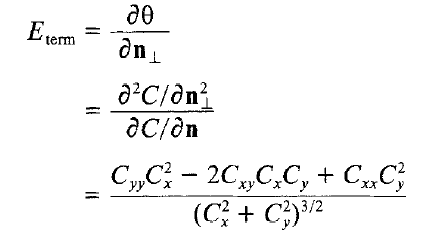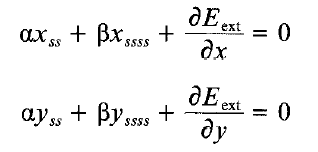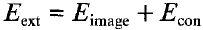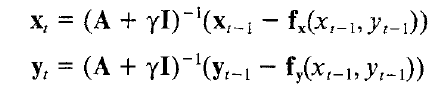snake是一种主动轮廓模型,笨妞对主动轮廓模型的理解:你先给它一个初始轮廓,模型以初始轮廓为基准逐步迭代,来改进图像的轮廓,使其更加精确。主动轮廓模型目前用到了2种:CV和snake。前者没有看算法内部的原理。而snake,以最原始的论文《Snakes: Active Contour Models》为出发点。
1. snake原理
snake在逐步迭代优化过程的目标是能量函数最小化,这个能量函数指的是轮廓能量和图像能量的总和(为什么要最小化这个能量总和,还不太清楚,论文也没有具体说)。snake的目标不像sobel、canny等找到整张图的轮廓。它只搜索你给出的初始轮廓附近,达到轮廓更精确的目标,至少原版的snake只能达到局部优化的目标。
能量函数:
其中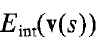
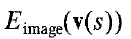
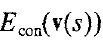
而内部能量由两部分构成:一阶导数的模(称为弹性能量)和二阶导数的模(弯曲能量)
为什么是这样的呢?据说是因为曲线曲率的关系,闭合的轮廓曲线中,凸曲线按照法向量的方向,具有向内的作用力;凹曲线法向量向外,具有向外的力。而曲率计算就是跟一阶导数、二阶导数相关的。很复杂,不甚理解。
在迭代过程中,弹性能量能快速的把轮廓压缩成光滑的圆;弯曲能量将轮廓拉成光滑的曲线或直线,他们的作用是保持轮廓的光滑和连续性。通常alpha越大,轮廓收敛越快;beta越大,轮廓越光滑。
外部图像能量作者分了三种:线性能量,通常更亮度相关;边缘能量,由图像的边缘组成,而边缘可以通过sobel算子计算;终端能量。
线性能量:
边缘能量:
终端(角点)能量:
通常可以根据更期望轮廓趋向于哪方面来选择以上三种能量。在迭代优化过程中,外部能量会使轮廓朝(灰度)高梯度位置靠近。而通常梯度高的位置都是图像中前景与背景的界限或者物体与物体之间、物体内部不同部分的界限,适合用于分割。
对于优化,优化的目标是总能量函数局部极小,通过能量函数极小或者迭代次数来控制迭代的终止。极小化能量函数通过欧拉方程计算解,作者在附录中用了数值方法进行推到,将欧拉方程推到为:
其中
引入外部能量:
再转化为每一步迭代演进过程:
A+ rI为五对角条带矩阵。
2. GVF snake
关于图像能量中line、edge、termatation计算其实都挺复杂的。反倒是计算梯度向量场简单一些。将图像能量由线、边缘、角点的能量替换为梯度向量场,就是GVF snake。
3. 程序
对于snake,skimage里面active_contour函数就是典型的snake算法,借用里面的实现程序:
import numpy as np
import scipy.linalg
from scipy.interpolate import RectBivariateSpline
from skimage.util import img_as_float
from skimage.filters import sobel
def active_contour(image, snake, alpha=0.01, beta=0.1,
w_line=0, w_edge=1, gamma=0.01,
bc='periodic', max_px_move=1.0,
max_iterations=2500, convergence=0.1):
"""Active contour model.
Active contours by fitting snakes to features of images. Supports single
and multichannel 2D images. Snakes can be periodic (for segmentation) or
have fixed and/or free ends.
The output snake has the same length as the input boundary.
As the number of points is constant, make sure that the initial snake
has enough points to capture the details of the final contour.
Parameters
----------
image : (N, M) or (N, M, 3) ndarray
Input image.
snake : (N, 2) ndarray
Initialisation coordinates of snake. For periodic snakes, it should
not include duplicate endpoints.
alpha : float, optional
Snake length shape parameter. Higher values makes snake contract
faster.
beta : float, optional
Snake smoothness shape parameter. Higher values makes snake smoother.
w_line : float, optional
Controls attraction to brightness. Use negative values to attract to
dark regions.
w_edge : float, optional
Controls attraction to edges. Use negative values to repel snake from
edges.
gamma : float, optional
Explicit time stepping parameter.
bc : {'periodic', 'free', 'fixed'}, optional
Boundary conditions for worm. 'periodic' attaches the two ends of the
snake, 'fixed' holds the end-points in place, and'free' allows free
movement of the ends. 'fixed' and 'free' can be combined by parsing
'fixed-free', 'free-fixed'. Parsing 'fixed-fixed' or 'free-free'
yields same behaviour as 'fixed' and 'free', respectively.
max_px_move : float, optional
Maximum pixel distance to move per iteration.
max_iterations : int, optional
Maximum iterations to optimize snake shape.
convergence: float, optional
Convergence criteria.
Returns
-------
snake : (N, 2) ndarray
Optimised snake, same shape as input parameter.
References
----------
.. [1] Kass, M.; Witkin, A.; Terzopoulos, D. "Snakes: Active contour
models". International Journal of Computer Vision 1 (4): 321
(1988).
Examples
--------
>>> from skimage.draw import circle_perimeter
>>> from skimage.filters import gaussian
Create and smooth image:
>>> img = np.zeros((100, 100))
>>> rr, cc = circle_perimeter(35, 45, 25)
>>> img[rr, cc] = 1
>>> img = gaussian(img, 2)
Initiliaze spline:
>>> s = np.linspace(0, 2*np.pi,100)
>>> init = 50*np.array([np.cos(s), np.sin(s)]).T+50
Fit spline to image:
>>> snake = active_contour(img, init, w_edge=0, w_line=1) #doctest: +SKIP
>>> dist = np.sqrt((45-snake[:, 0])**2 +(35-snake[:, 1])**2) #doctest: +SKIP
>>> int(np.mean(dist)) #doctest: +SKIP
25
"""
max_iterations = int(max_iterations)
if max_iterations <= 0:
raise ValueError("max_iterations should be >0.")
convergence_order = 10
valid_bcs = ['periodic', 'free', 'fixed', 'free-fixed',
'fixed-free', 'fixed-fixed', 'free-free']
if bc not in valid_bcs:
raise ValueError("Invalid boundary condition.\n" +
"Should be one of: "+", ".join(valid_bcs)+'.')
img = img_as_float(image)
height = img.shape[0] width = img.shape[1]
RGB = img.ndim == 3
# Find edges using sobel:
if w_edge != 0:
if RGB:
edge = [sobel(img[:, :, 0]), sobel(img[:, :, 1]),
sobel(img[:, :, 2])]
else:
edge = [sobel(img)]
for i in range(3 if RGB else 1):
edge[i][0, :] = edge[i][1, :]
edge[i][-1, :] = edge[i][-2, :]
edge[i][:, 0] = edge[i][:, 1]
edge[i][:, -1] = edge[i][:, -2]
else:
edge = [0]
# Superimpose intensity and edge images:
if RGB:
img = w_line*np.sum(img, axis=2) \
+ w_edge*sum(edge)
else:
img = w_line*img + w_edge*edge[0]
# Interpolate for smoothness:
intp = RectBivariateSpline(np.arange(img.shape[1]),
np.arange(img.shape[0]),
img.T, kx=2, ky=2, s=0)
x, y = snake[:, 0].astype(np.float), snake[:, 1].astype(np.float)
xsave = np.empty((convergence_order, len(x)))
ysave = np.empty((convergence_order, len(x)))
# Build snake shape matrix for Euler equation
n = len(x)
a = np.roll(np.eye(n), -1, axis=0) + \
np.roll(np.eye(n), -1, axis=1) - \
2*np.eye(n) # second order derivative, central difference
b = np.roll(np.eye(n), -2, axis=0) + \
np.roll(np.eye(n), -2, axis=1) - \
4*np.roll(np.eye(n), -1, axis=0) - \
4*np.roll(np.eye(n), -1, axis=1) + \
6*np.eye(n) # fourth order derivative, central difference
A = -alpha*a + beta*b
# Impose boundary conditions different from periodic:
sfixed = False
if bc.startswith('fixed'):
A[0, :] = 0
A[1, :] = 0
A[1, :3] = [1, -2, 1]
sfixed = True
efixed = False
if bc.endswith('fixed'):
A[-1, :] = 0
A[-2, :] = 0
A[-2, -3:] = [1, -2, 1]
efixed = True
sfree = False
if bc.startswith('free'):
A[0, :] = 0
A[0, :3] = [1, -2, 1]
A[1, :] = 0
A[1, :4] = [-1, 3, -3, 1]
sfree = True
efree = False
if bc.endswith('free'):
A[-1, :] = 0
A[-1, -3:] = [1, -2, 1]
A[-2, :] = 0
A[-2, -4:] = [-1, 3, -3, 1]
efree = True
# Only one inversion is needed for implicit spline energy minimization:
inv = scipy.linalg.inv(A+gamma*np.eye(n))
# Explicit time stepping for image energy minimization:
for i in range(max_iterations):
fx = intp(x, y, dx=1, grid=False)
fy = intp(x, y, dy=1, grid=False)
if sfixed:
fx[0] = 0
fy[0] = 0
if efixed:
fx[-1] = 0
fy[-1] = 0
if sfree:
fx[0] *= 2
fy[0] *= 2
if efree:
fx[-1] *= 2
fy[-1] *= 2
xn = np.dot(inv, gamma*x + fx)
yn = np.dot(inv, gamma*y + fy)
# Movements are capped to max_px_move per iteration:
dx = max_px_move*np.tanh(xn-x)
dy = max_px_move*np.tanh(yn-y)
if sfixed:
dx[0] = 0
dy[0] = 0
if efixed:
dx[-1] = 0
dy[-1] = 0
x += dx
y += dy
x[x<0] = 0 y[y<0] = 0 x[x>(height-1)] = height - 1 y[y>(width-1)] = width - 1
# Convergence criteria needs to compare to a number of previous
# configurations since oscillations can occur.
j = i % (convergence_order+1)
if j < convergence_order:
xsave[j, :] = x
ysave[j, :] = y
else:
dist = np.min(np.max(np.abs(xsave-x[None, :]) +
np.abs(ysave-y[None, :]), 1))
if dist < convergence:
break
return np.array([x, y]).T这个程序有个bug,没有对新计算出的轮廓做约束,这样的话如果初始snake比较靠近图像的边,那么轮廓就会溢出到图像外。红色部分是个人做的修改。
另外一个简化的gvf snake程序
file_name = '24_82_11.bmp'
#file_path = os.path.join('cell_split/23-2018-05-1708.57.22', file_name)
img = skimage.color.rgb2gray(skimage.data.imread(file_name))
f = filters.gaussian_gradient_magnitude(img,2.0)
fx = filters.gaussian_filter(f,2.0,(1,0))
fy = filters.gaussian_filter(f,2.0,(0,1))
u = fx.copy()
v = fy.copy()
mu = 0.1
for i in range(10000):
m = (fx**2+fy**2)
ut = mu*filters.laplace(u)-(u-fx)*m
vt = mu*filters.laplace(v)-(v-fy)*m
u += ut
v += vt
t = np.linspace(0,2*np.pi,50)
for t in range(5000):
x2 = filters.gaussian_filter(path,1.0,(2,0),mode='wrap')
x4 = filters.gaussian_filter(x2,1.0,(2,0),mode='wrap')
dx = np.array([u[int(x),int(y)] for y,x in path])
dy = np.array([v[int(x),int(y)] for y,x in path])
delta = np.array([dx,dy]).T
path += 0.001*x2-0.001*x4+1.0*delta
#print(path.shape)
path[:,0][path[:,0]>129] = 129
path[:,1][path[:,1]>105] = 105这个gvf snake基本的骨架是对的,但是太简单了,效果确实不好。
今天的文章snake算法总结分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/8479.html