关系数据库理论
关系模式的组成
一个关系模式应当是一个五元组R(U,D,DOM,F)
这里R是符号化的元组语义
- U为一组属性
- D为属性组U中的属性所来自的域
- DOM为属性到域的映射
- F为属性组U上一组数据依赖(是一组数据依赖的集合)
由于D,DOM与模式涉及关系不大,因此本章中把关系模式看作一个三元组:R<U, F>,当且仅当U上一个关系r满足F时,r称为关系模式R<U, F>的一个关系
第一范式1NF
每一个分量必须是不可分的数据项
数据依赖
定义:数据依赖是一个关系内部属性和属性之间的一种约束关系。这种约束关系是通过属性间值的相等与否来体现出来的数据间的相互关系。
人已经提出了许多类型的数据依赖,其中最重要的是函数依赖和多值依赖。其中:
函数依赖:属性间的依赖关系类似于数学中的函数f(x),自变量x确定以后,相应的函数值y也就唯一的确定了。
函数依赖关系设置有误关系模式容易存在的问题
-
数据冗余
-
更新异常
-
插入异常
-
删除异常
一个好的模式应当不会发生插入异常,删除异常和更新异常,数据冗余尽可能少
规范化
以上问题都是由于存在于模式中的某些数据依赖引起的,所以规范化要讨论的问题,就是用规范化理论改造关系模式来消除其中不合适的数据依赖。
函数依赖
定义:设R(U)是属性集U上关系模式,X,Y是U的子集。若多R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等,而在Y的属性值不等,则称X函数确定Y或Y函数依赖于X,记为X—>Y。即t2[x1]=y2[x2]则t1[Y]=t2[Y]。
PS:函数依赖不是关系模式R上的某个或某些关系满足的约束条件,是R上的所有的一切关系都要满足
一些概念:
-
X->Y,但Y∈X,则称X->Y是平凡函数依赖
-
X->Y,但Y不属于X,则称X->Y是非平凡函数依赖
-
在R(U)中,若X->Y,并且对于X的任何一个真子集X‘,都有X’不决定Y,则称Y对X是完全函数依赖,决定方只有一个时必为完全函数依赖。例如:course表中cno->cname
-
若X->Y,但Y不完全函数依赖于X,则称Y对X部分函数依赖,决定方必为2个或2个以上。例如:student表中(sno,ssex)->sname
-
若x->y 且y->x则记为x<->y,记为相互依赖,例如:一个班只有一个班长,一个班长也只对应一个班级,二者一一对应。
-
在R(U)中,如果X->Y(Y不属于X,否则平凡依赖),Y不决定X(否则相互依赖),Y->Z(Z不属于Y否则平凡依赖)则称Z对X传递函数依赖。
码
候选码:如果关系中的某一属性或属性组的值能唯一地标识一个元组,则称该属性或属性组组为候选码; 例如在不重名的student表中,候选码有两个:sno和sname,但在sc表中候选码只有一个,即为(sno,cno)属性组。
主码:如果一个关系有多个候选码,则选定其中一个为主码;
主属性:包含在任何一个候选码中的属性;
非主属性:不包含在任何候选码中的属性称为非主属性或非码属性。
全码:整个属性组都是候选码
PS:在R<U ,F>中,设K为R(U)中的属性或属性集合,若K完全函数依赖于K,则K为R的候选码。如果U函数依赖于K,即K->U,则称K为超码。候选码是最小超码。
外码:关系模式R中属性或属性组X并非R的码,但X是另一个关系模式的码,则称X为R的外部码,也称外码。主表是R表,从表是另外一个关系模式的表。例如:sc(sno,cno,grade)是sno不是sc的码,却是student的码,所以sno是sc的外码。
范式
关系数据库中的关系是要满足一定要求的,满足不同程度要求的为不同范式。
范式是符合某一种级别的关系模式的集合。
一个低一级的范式的关系通过模式分解可以转换为若干个高一级范式的关系模式的集合,这种过程就叫规范化
第二范式2NF
定义:若R∈1NF,且每个非主属性完全函数依赖于任何一个候选码,则R∈2NF。
终极要求就是:消除部分依赖。
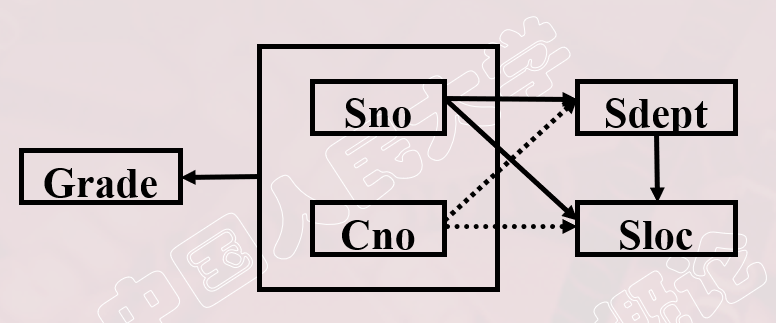
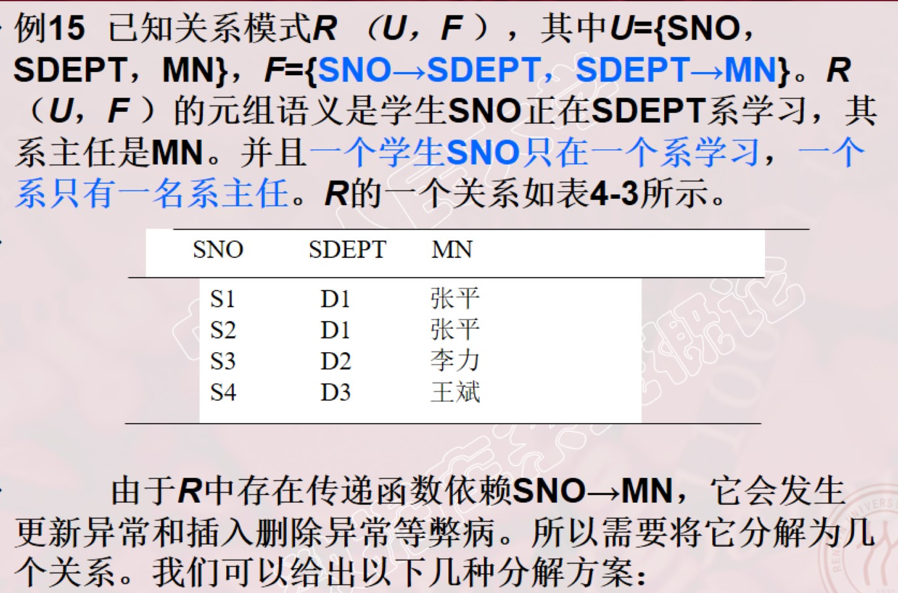
S-L-C(Sno,Sdept,Sloc,Cno,Grade), Sloc为学生的住处,并且每个系的学生住在同一个地方。S-L-C的码为(Sno,Cno)。
函数依赖有:
- (Sno,Cno)→Grade
- Sno→Sdept, (Sno,Cno)→Sdept
- Sno→Sloc, (Sno,Cno)→Sloc
- Sdept→Sloc
非主属性Sdept、Sloc并不完全依赖于码。关系模式S-L-C不属于2NF。
会导致问题如下:
出现这种问题的原因:
例子中有两类非主属性:
- 一类如Grade,它对码完全函数依赖
- 另一类如Sdept、Sloc,它们对码不是完全函数依赖
解决方法:
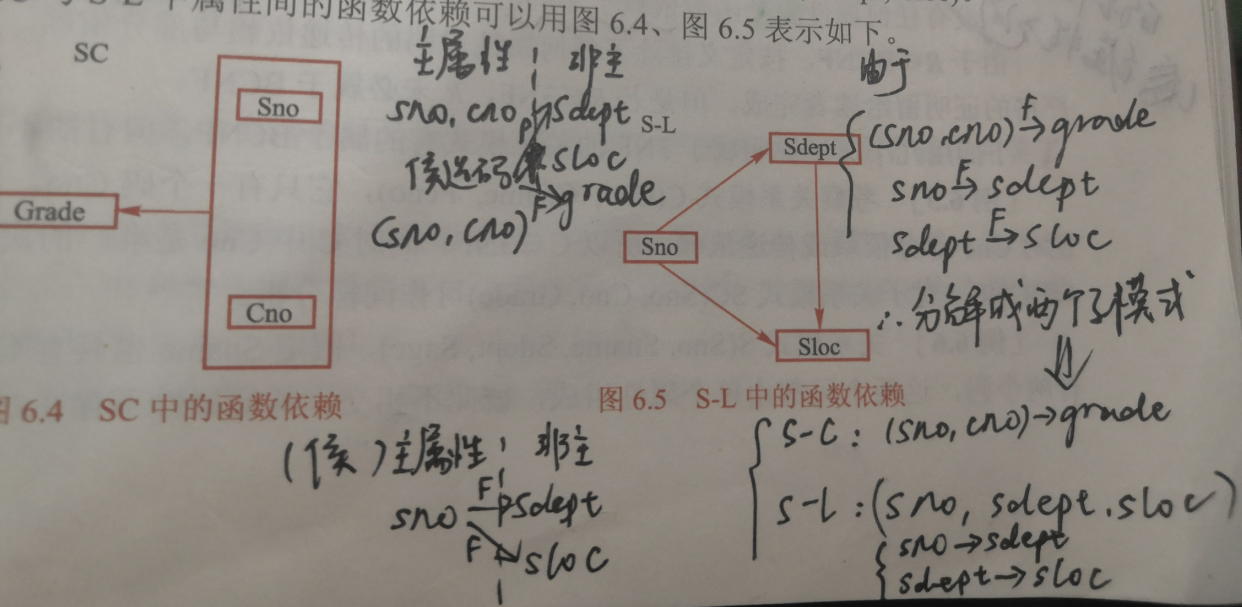
用投影分解把关系模式S-L-C分解成两个关系模式
- SC(Sno,Cno,Grade)
- S-L(Sno,Sdept,Sloc)
SC的码为(Sno,Cno),SL的码为Sno,这样使得非主属性对码都是完全函数依赖了
第三范式3NF
定义:设关系模式R<U,F>∈1NF,若R中不存在这样的码X、属性组Y及非主属性Z(Z ⊇ Y), 使得X→Y,Y→Z成立,Y 不决定X不成立,则称R<U,F> ∈ 3NF。
终极目的:消除部份依赖,传递依赖
PS:3NF只讨论了非主属性的依赖关系,所以要在3NF的基础上讨论主属性的依赖关系,所以就有了BCNF。
例子:
SC没有传递依赖,因此SC ∈ 3NF
S-L中Sno →Sdept( Sdept ↛ Sno), Sdept→Sloc,可得Sno → Sloc。
解决的办法是将S-L分解成:
- S-D(Sno,Sdept)∈ 3NF
- D-L(Sdept,Sloc)∈ 3NF
BC范式BCNF
背景:BCNF(Boyce Codd Normal Form)由Boyce和Codd提出,比3NF更进了一步。通常认为BCNF是修正的第三范式,有时也称为扩充的第三范式。
定义:设关系模式R<U,F>∈1NF,若X →Y且Y 不属于 X时X必含有码,则R<U,F>∈BCNF。
换言之,在关系模式R<U,F>中,如果每一个决定属性集都包含候选码,则R∈BCNF。
如果一个关系数据库中的所有关系模式都属于BCNF,那么在函数依赖范畴内,它已实现了模式的彻底分解,达到了最高的规范化程度,消除了插入异常和删除异常。3NF的“不彻底”性表现在可能存在主属性对码的部分依赖和传递依赖。
性质:
- 所有非主属性都完全函数依赖于每个候选码
- 所有主属性都完全函数依赖于每个不包含它的候选码
- 没有任何属性完全函数依赖于非码的任何一组属性
例1:
考察关系模式C(Cno,Cname,Pcno)
它只有一个码Cno,没有任何属性对Cno部分依赖或传递依赖,所以C∈3NF。同时C中Cno是唯一的决定因素,所以C∈BCNF。
例2:
关系模式S(Sno,Sname,Sdept,Sage),假定Sname也具有唯一性,那么S就有两个码,这两个码都由单个属性组成,彼此不相交。
其他属性不存在对码的传递依赖与部分依赖,所以S∈3NF。
同时S中除Sno,Sname外没有其他决定因素,所以S也属于BCNF。
例3:
关系模式SJP(S,J,P)中,S是学生,J表示 课程,P表示名次。每一个学生选修每门课程的成绩有一定的名次,每门课程中每一名次只有一个学生(即没有并列名次)。
由语义可得到函数依赖: (S,J)→P;(J,P)→S (S,J)与(J,P)都可以作为候选码。
关系模式中没有属性对码传递依赖或部分依赖,所以SJP∈3NF。
除(S,J)与(J,P)以外没有其他决定因素,所以SJP∈BCNF。
例4:
关系模式STJ(S,T,J)中,S表示学生,T表示教师,J表示课程。每一教师只教一门课。每门课有若干教师,某一学生选定某门课,就对应一个固定的教师。
由语义可得到函数依赖:(S,J)→T;(S,T)→J;T→J
这里(S,J)和(S,T)都是候选码,T不是候选码,因为T无法决定S
因为没有任何非主属性对码传递依赖或部分依赖,STJ ∈ 3NF。
因为T是决定因素,而T不包含码,所以STJ ∈ BCNF关系。
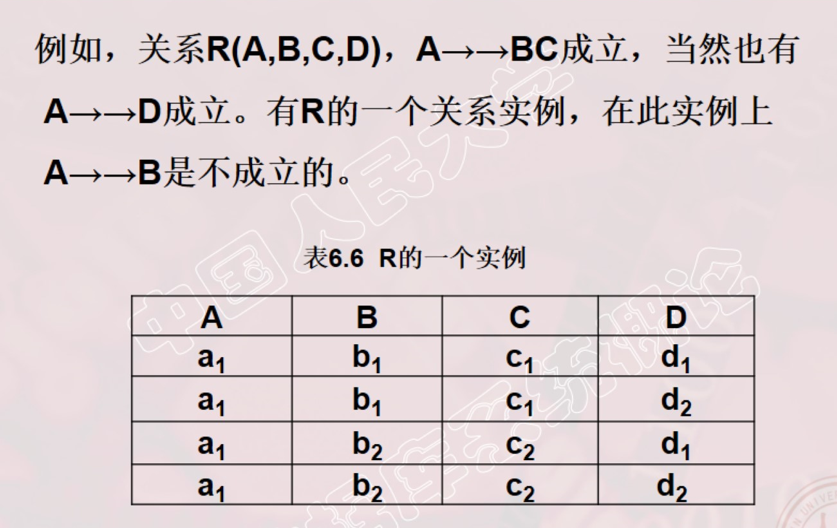
多值依赖
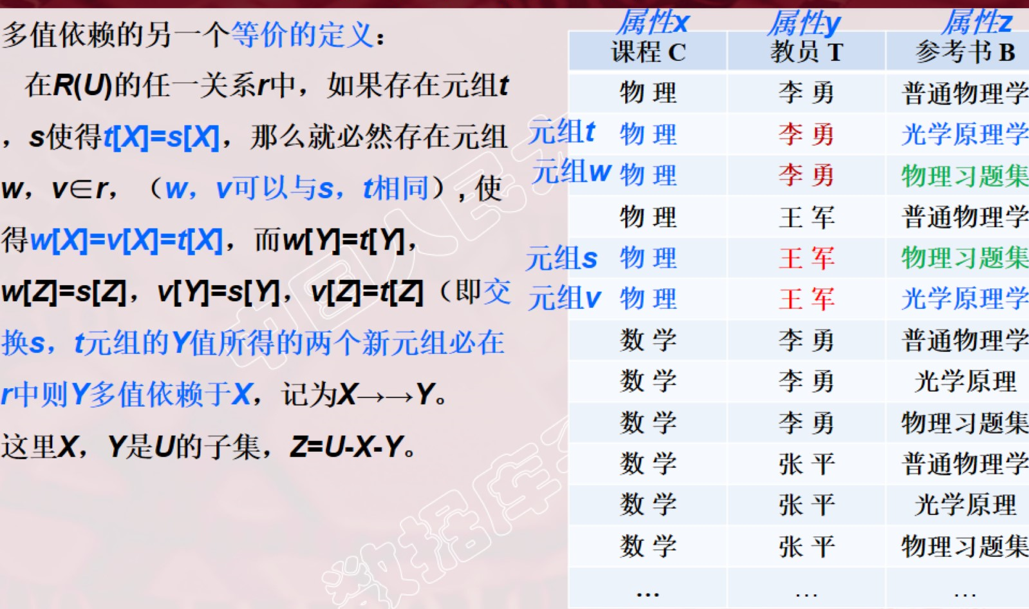
定义:设R(U)是属性集U上的一个关系模式。X,Y,Z是U的子集,并且Z=U-X-Y。关系模式R(U)中多值依赖X→→Y成立,当且仅当对R(U)的任一关系r,给定的一对(x,z)值,有一组Y的值,这组值仅仅决定于x值而与z值无关。
例 :Teaching(C, T, B)。对于C的每一个值,T有一组值与之对应,而不论B取何值。因此T多值依赖于C,即C→→T。
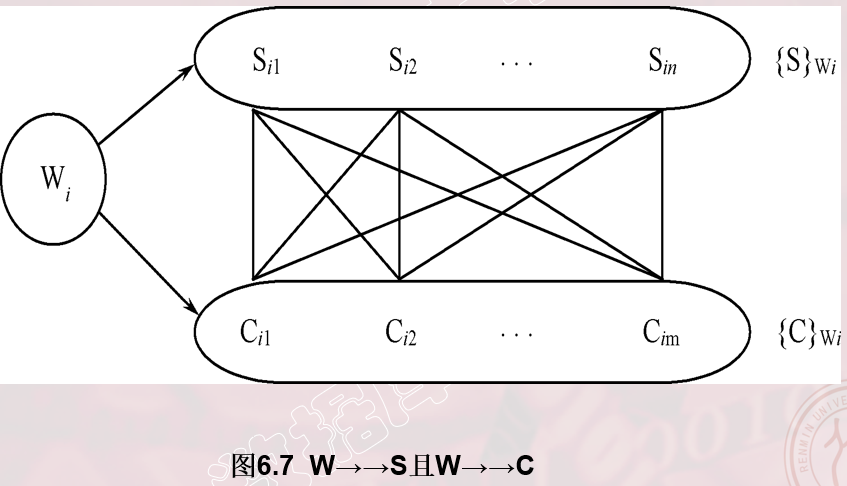
平凡多值依赖和非平凡多值依赖
若X→→Y,而Z为空,则称X→→Y为平凡多值依赖。否则称X→→Y为非平凡多值依赖。
性质
- 传递性
- 函数依赖可以看作是多值依赖的特殊情况
- 对称性
多值依赖与函数依赖的区别
(1)多值依赖的有效性与属性集的范围有关
(2)若函数依赖X→Y在R (U)上成立,则对于任何Y‘ Y均有X→Y’ 成立。多值依赖X→→Y若在R(U)上成立,不能断言对于任何Y’ Y有X→→Y’ 成立。
4NF
定义:关系模式R<U,F>∈1NF,如果对于R的每个非平凡多值依赖X→→Y(Y ⊈ X),X都含有码,则R<U,F>∈4NF。
4NF就是限制关系模式的属性之间不允许有非平凡且非函数依赖的多值依赖。4NF所允许的非平凡多值依赖实际上是函数依赖。
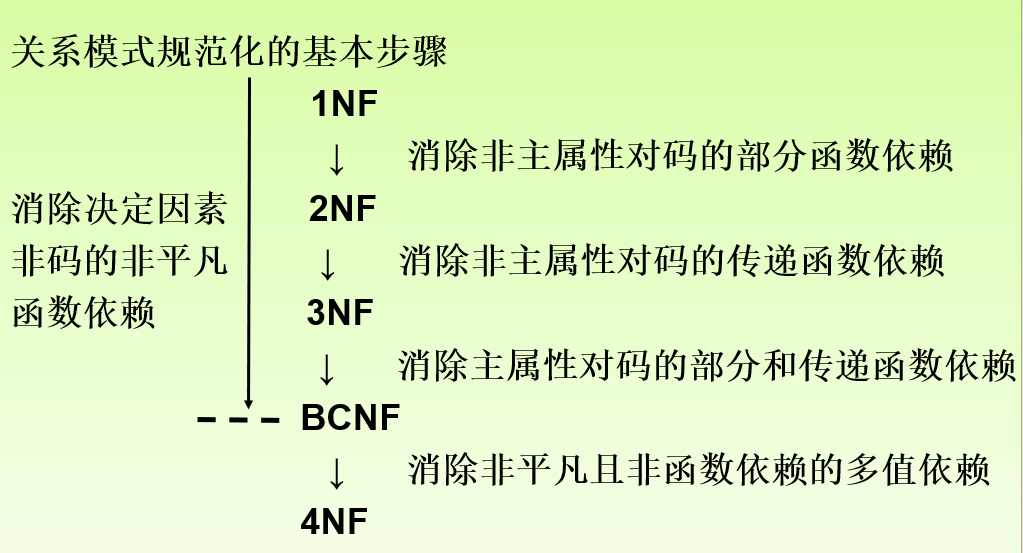
规范化小结
规范化的基本思想是逐步消除数据以来中不合适的部分。
数据依赖的公理系统
定义:对于满足一组函数依赖F的关系模式 R <U,F>,其任何一个关系r,若函数依赖X→Y都成立(即r中任意两元组t、s,若t[X]=s[X],则 t[Y]=s[Y]),则称F逻辑蕴涵X →Y。
Armstrong公理系统
设U为属性集总体,F是U上的一组函数依赖, 于是有关系模式R <U,F >。对R <U,F> 来说有以下的推理规则:
- 自反律(reflexivity rule):若Y 属于 X 属于 U,则X →Y 为F所蕴涵。
- 增广律(augmentation rule):若X→Y为F所蕴涵,且Z 属于U,则XZ→YZ 为F所蕴涵。
- 传递律(transitivity rule):若X→Y及Y→Z为F所蕴涵,则X→Z 为F所蕴涵。
定理 6.1
阿姆斯特朗推理的规则是正确的
证明
自反律证明:
设Y 属于X 属于 U 。
对R <U,F> 的任一关系r中的任意两个元组t、s:
若t[X]=s[X],由于Y 属于X,有t[Y]=s[Y],
所以X→Y成立,
自反律得证。
增广律证明:
设X→Y为F所蕴涵,且Z 属于U。
对R<U,F> 的任一关系r中任意的两个元组t、s:
若t[XZ]=s[XZ],则有t[X]=s[X]和t[Z]=s[Z];
由X→Y,于是有t[Y]=s[Y],
所以t[YZ]=s[YZ],XZ→YZ为F所蕴涵,
增广律得证。
传递律证明:
设X→Y及Y→Z为F所蕴涵。
对R<U,F> 的任一关系r中的任意两个元组t、s:
若t[X]=s[X],由于X→Y,有t[Y]=s[Y];
再由Y→Z,有t[Z]=s[Z],
所以X→Z为F所蕴涵,
传递律得证。
三条推理规则
-
合并规则(union rule):由X→Y,X→Z,有X→YZ。
-
伪传递规则(pseudo transitivity rule):由X→Y,WY→Z,有XW→Z。
-
分解规则(decomposition rule):由X→Y及Z属于Y,有X→Z。
引理6.1
X→A1 A2…Ak成立的充分必要条件是X→Ai成立(i=1,2,…k)
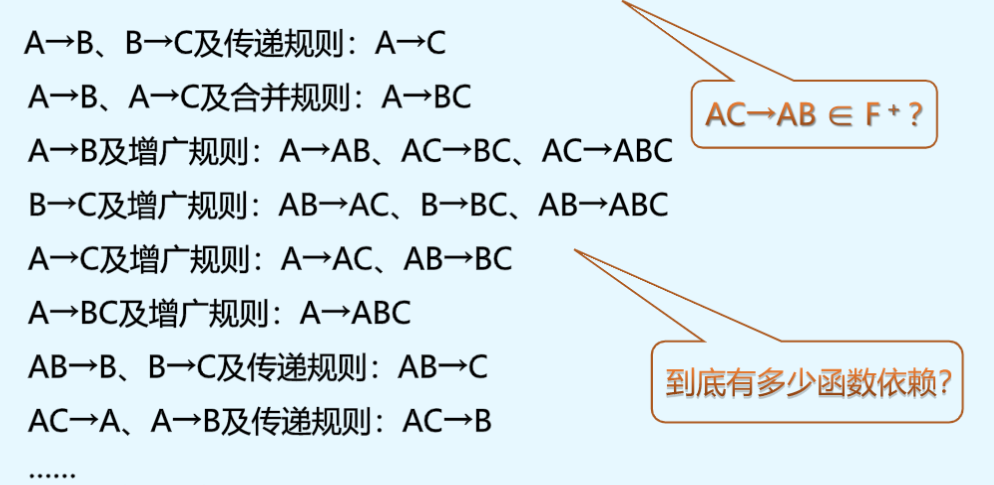
闭包
定义6.12(F闭包)
在关系模式R<U,F>中为F所逻辑蕴涵的函数依赖的全体叫作F的闭包,记为F +。
定义6.13(X闭包)
设F为属性集U上的一组函数依赖,X、Y 属于U, XF+={ A|X→A能由F根据Armstrong公理导出},XF+称为属性集X关于函数依赖集F的闭包。
引理6.2
设F为属性集U上的一组函数依赖,X、Y 属于 U,X→Y能由F根据Armstrong公理导出的充分必要条件是Y 属于XF+。
算法6.1(求X闭包)
如何求属性集X(X 属于U)关于U上的函数依赖集F的闭包XF+ ?
例子:
有效性完备性
定理6.2(有效性完备性)
阿姆斯特朗公理系统是有效的、完备的。
有效性:由F 出发根据Armstrong公理推导出来的每一个函数依赖一定在F +中
完备性:F +中的每一个函数依赖,必定可以由F出发根据Armstrong公理推导出来
最小函数依赖集
定义6.14(闭包等价)
如果G+=F+,就说函数依赖集F覆盖G(F是G的覆盖,或G是F的覆盖),或F与G等价。两个函数依赖集等价是指它们的闭包等价
证明:
引理6.3
F+ = G+ 的充分必要条件是F 属于 G+和G属于 F+ 。
定义6.15(最小函数依赖)
如果函数依赖集F满足下列条件,则称F为一个极小函数依赖集,亦称为最小依赖集或最小覆盖。
(1)F中任一函数依赖的右部仅含有一个属性。
(2)F中不存在这样的函数依赖X→A, 使得F与
F-{X→A}等价。
(3)F中不存在这样的函数依赖X→A, X有真
子集Z使得F-{X→A}∪{Z→A}与F等价。
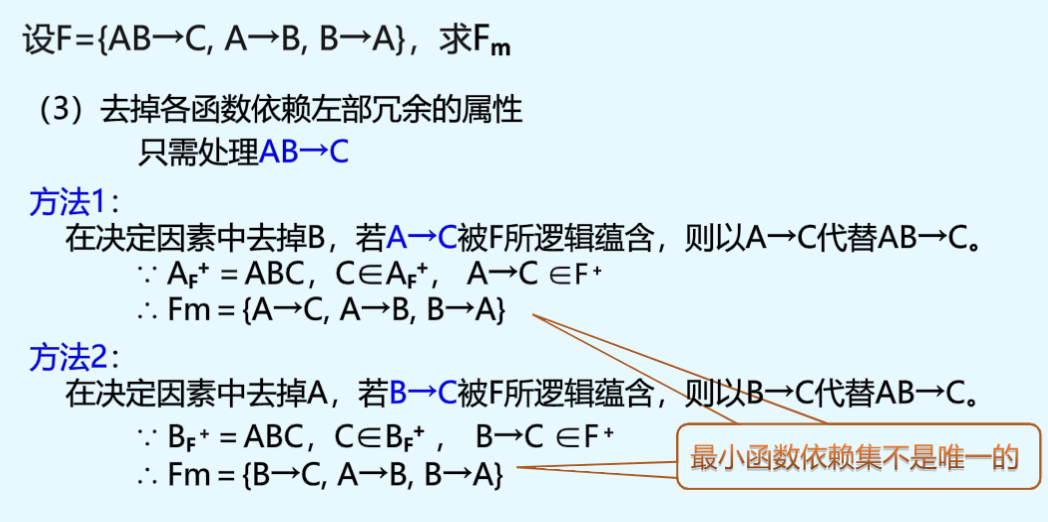
寻找最小函数依赖集算法描述
例子:
定理6.3
每一个函数依赖集F均等价于一个极小函数依赖集Fm。此Fm称为F的最小依赖集。
PS:在R<U,F>中可以用与F等价的依赖集G来取代F
原因:两个关系模式R,<U,F>,R,<u,G>,如果F与G等价,那么R,的关系一定是Rz的关系。反过来,R的关系也一定是R,的关系。
候选码的确定
决定方为X或X的子集,X1→Y,X’→A且X‘∈X1则X1→AY(无限循环),X1→A1A2A3……An。若A1A2……An=U则说明X1为候选码。
例子:
寻找候选键K的方法
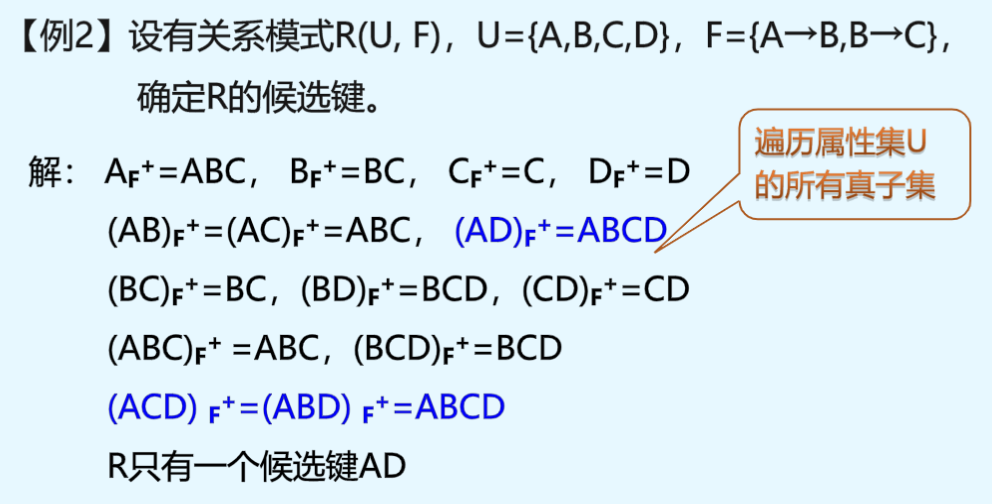
- 方法一:遍历属性集U的所有真子集
- 方法二:逐─排除U中冗余属性
- 方法三:快速确定K中主属性
方法一例子:
方法二例子:
方法三例子:
L类:仅出现在函数依赖左部的属性;
R类:仅出现在函数依赖右部的属性;
LR类:在函数依赖左右两边均出现的属性;
N类:在函数依赖左右两边均未出现的属性。
- 定理1:若X是R的L类属性,则X必为R的主属性。
- 定理2:若X是R的R类属性,则X必为R的非主属性。
- 定理3:若X是R的N类属性,则X必为R的主属性。
模式分解
关系模式设计得不好会带来很多问题。为了避免这些问题的发生,有时需要把一个关系模式分解为几个关系模式,这就是关系模式的分解。把低一级的关系模式分解为若干个高一级的关系模式的方法不是唯一的。只有能够保证分解后的关系模式与原关系模式等价,分解方法才有意义。
三种模式分解等价的定义:
- 分解具有无损连接性:通过自然联接可以恢复到原来的关系模式
- 分解要保持函数依赖:分解后的关系模式能保持原有的函数依赖
- 分解既要保持函数依赖,又要具有无损连接性
定义6.16 (模式分解ρ)
关系模式R<U,F>的一个分解ρ :ρ={ R1<U1,F1>,R2<U2,F2>,…,Rn<Un,Fn>}
定义6.17
模式分解的三个定义
- 分解具有无损连接性
- 分解要保持函数依赖性
- 分解既要保持函数依赖,又要保持无损连接性。
这三个定义是实行分解的三条不同的准则,按照不同的分解准则,模式所能达到的分离程度各不相同,各种范式就是对分离程度的测度。
例子:
无损连接
定义:设ρ={ R1(U1,F1),R2(U2,F2),…,Rk(Uk,Fk)}是R (U,F )的一个分解,r是R (U,F )的一个关系。定义mρ(r)=∏R1(r)⋈ ΠR2(r)⋈…⋈ ΠRk(r),即mρ(r)是r在ρ中各关系模式上投影的自然连接。这里ΠRi(r)={t.Ui│t属于r}。
定义6.18(无损连接)
把分解后的关系做自然联接必然包含分解前的关系,这就是说分解是不会丢失信息的。因为此处的分解是用投影把原关系的某些信息取出来,对每列属性值都不会丢失信息,因而分解后再做自然联接其结果必然包含原来的关系,而且有可能多出来一些无效元组信息。
例子:
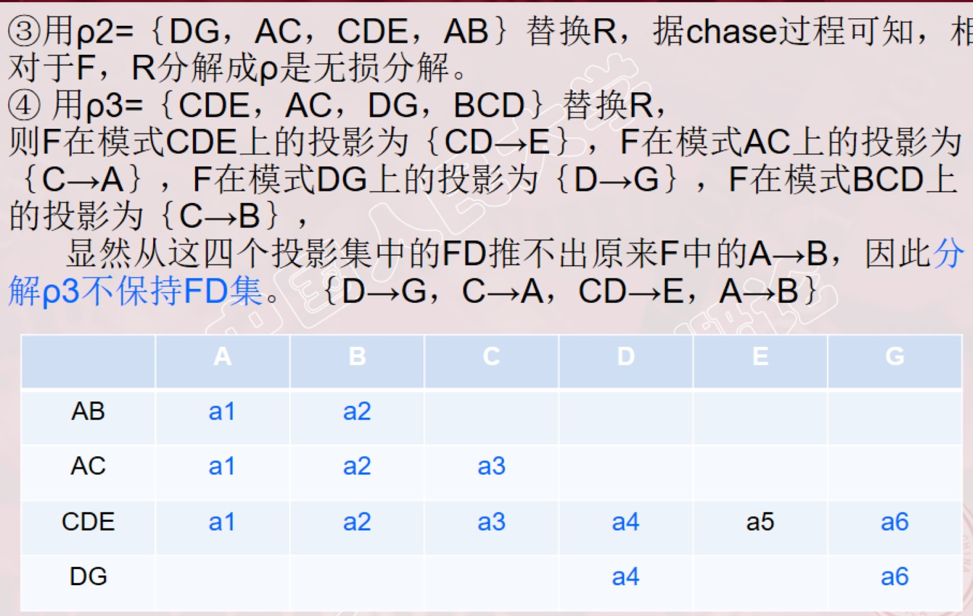
算法6.2(判断无损连接)
判别一个分解的无损连接性
方法(构造法):
- 构造一个k行n列的表。每一行对应分解中的一个关系模式,即第i行对应关系模式Ri;每一列对应一个属性名,即第j列对应于属性名Aj。如果Aj∈Ui,则在第i行第j列上填上符号aj,否则填上符号bij。
- 反复检查F中的每一个函数依赖FDi,并修改表中元素。其方法为:取F中的每一函数依赖X→Y,在X所对应的列中寻找具有相同符号的那些行,然后将这些行中Y列上的值改为相同的符号。如果其中有aj,则将这些列上的bij全部改为aj,若其中无aj,则改为bij,其中i是这些行的行号最小值。
- 如果在某次更改后有一行是全a,即a1,a2,…,an,则算法终止,ρ具有无损联接性;如果直到表格不能再修改为止也没有发现这样的行,则ρ不具有无损联接性。
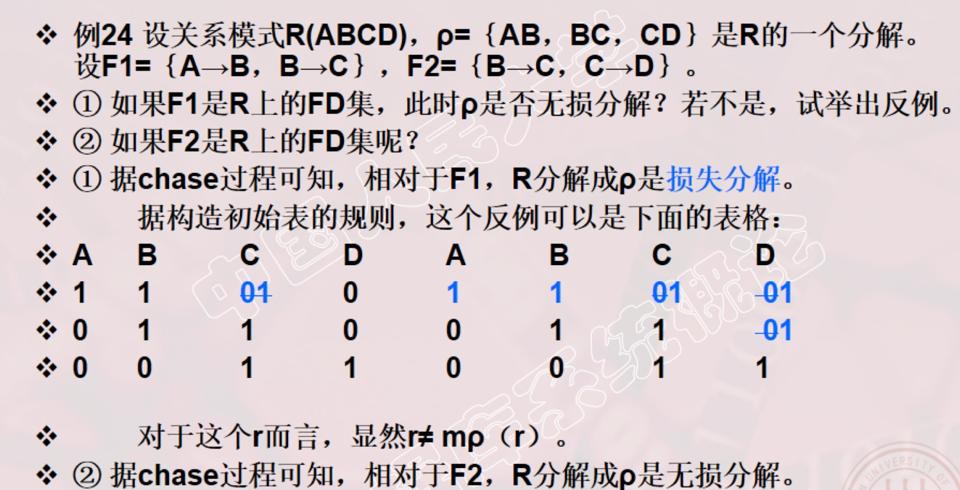
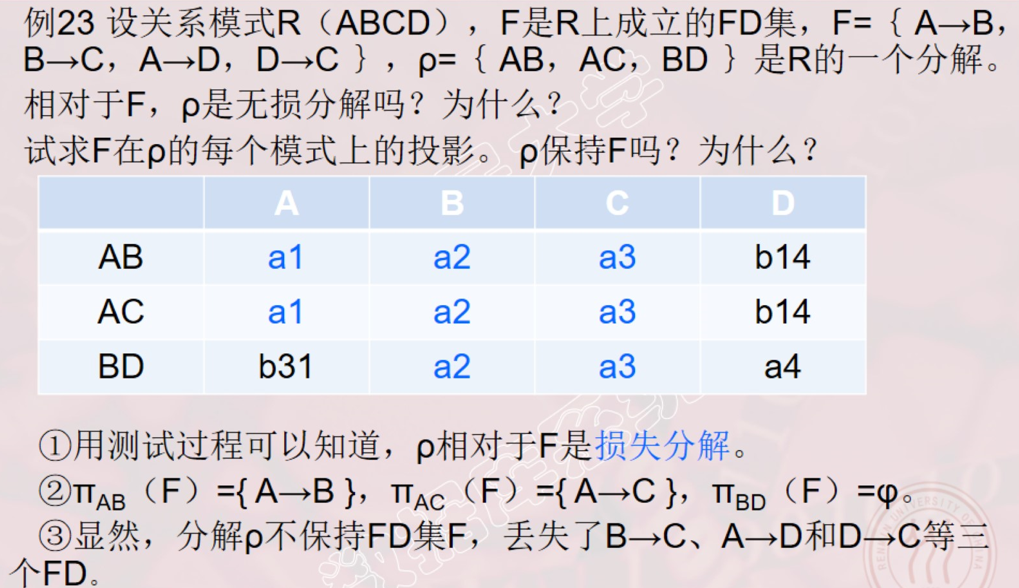
例子:
定理6.4
算法终止时,表中有一行a1,a2……an则p为无损连接。
定理6.5
对于R<U,F> 的一个分解ρ={R1<U1,F1>,R2<U2,F2>},如果U1∩U2→U1-U2∈F+或U1∩U2→U2-U1∈F+,则ρ具有无损连接性
(即属性集的交集能决定其属性集的差集是蕴含在函数依赖集F中)
函数依赖
定义6.19(函数依赖)
设关系模式R (U,F )的一个分解ρ={ R1(U1,F1),R2(U2,F2),…,Rk(Uk,Fk)},如果F等价于(∪Fi) ,则称分解ρ具有依赖保持性。
PS:保持函数依赖和无损连接没有必然的联系。
例子:
- 第1种分解方法既不具有无损连接性,也未保持函数依赖,它不是原关系模式的一个等价分解
- 第2种分解方法既未保持函数依赖,也不具有无损连接性
- 第3种分解方法具有无损连接性,但未持函数依赖
- 第4种分解方法既具有无损连接性,又保持了函数依赖
算法6.3(转化为3NF保持函数依赖)
如果要求分解保持函数依赖,那么模式分解总可以达到3NF,但不一定能达到BCNF;如果要求分解既保持函数依赖,又具有无损联接性,那么模式分离可以达到3NF,但不一定能达到BCNF。
方法:
- 最小函数依赖集
- 找出“孤儿”属性U0,剩下属性记为U
- 相同左部原则进行合并
- 每一组函数依赖所涉及的全部属性形成一个属性集Ui。若Ui包含于Uj(i不等于j)就去掉Ui。
例子:
算法6.4(转化3NF保持函数依赖和无损连接)
方法:
- 最小函数依赖集
- 相同左部原则进行合并
- 找出“孤儿”属性,确定候选码为(左部+孤儿)。若无孤儿属性则找出函数依赖关系中的候选码。
- 模式分解为p∪(候选码)= M
- 若某个UI,候选码包含于Ui,则将M中把(候选码)去掉,只留下p即为最后结果。若Ui包含于X,则在M中把p中的Ui去掉,留下即为最终结果。
例子:
模式分解例题
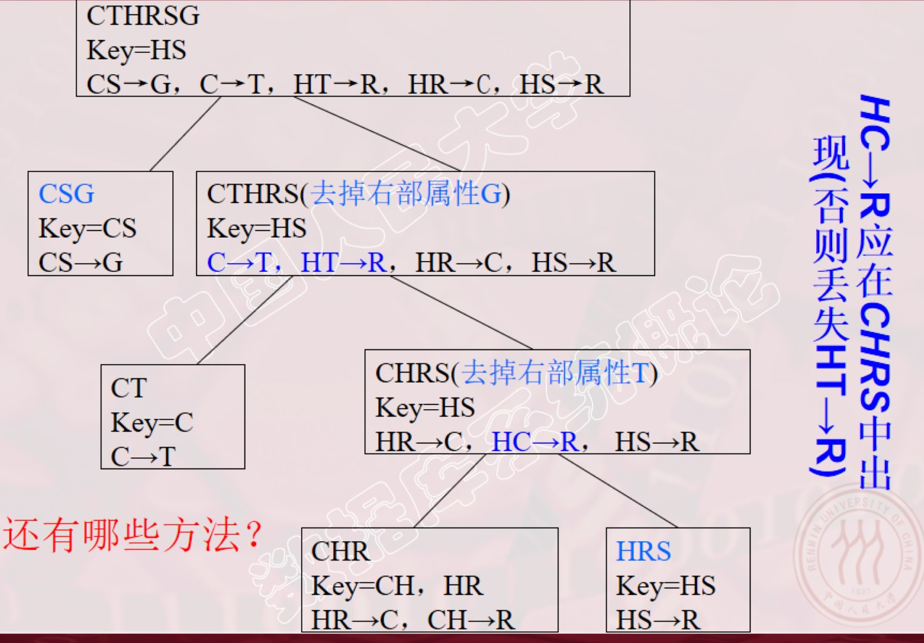
算法6.5(转换为BCNF的无损连接)
方法:
- 最小函数依赖
- 找到关系模式中候选码
- 从F中随机找一个X→Y,保证其为BCNF分离出去。剩余的再进行分离,如若存在已分离出去的函数依赖的非主属性,则需要替换其中的非主属性为分离出去函数依赖的主属性。直到分离到最后都为BCNF结束。
例子:
模式分解原则
今天的文章关系数据库理论分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/8506.html