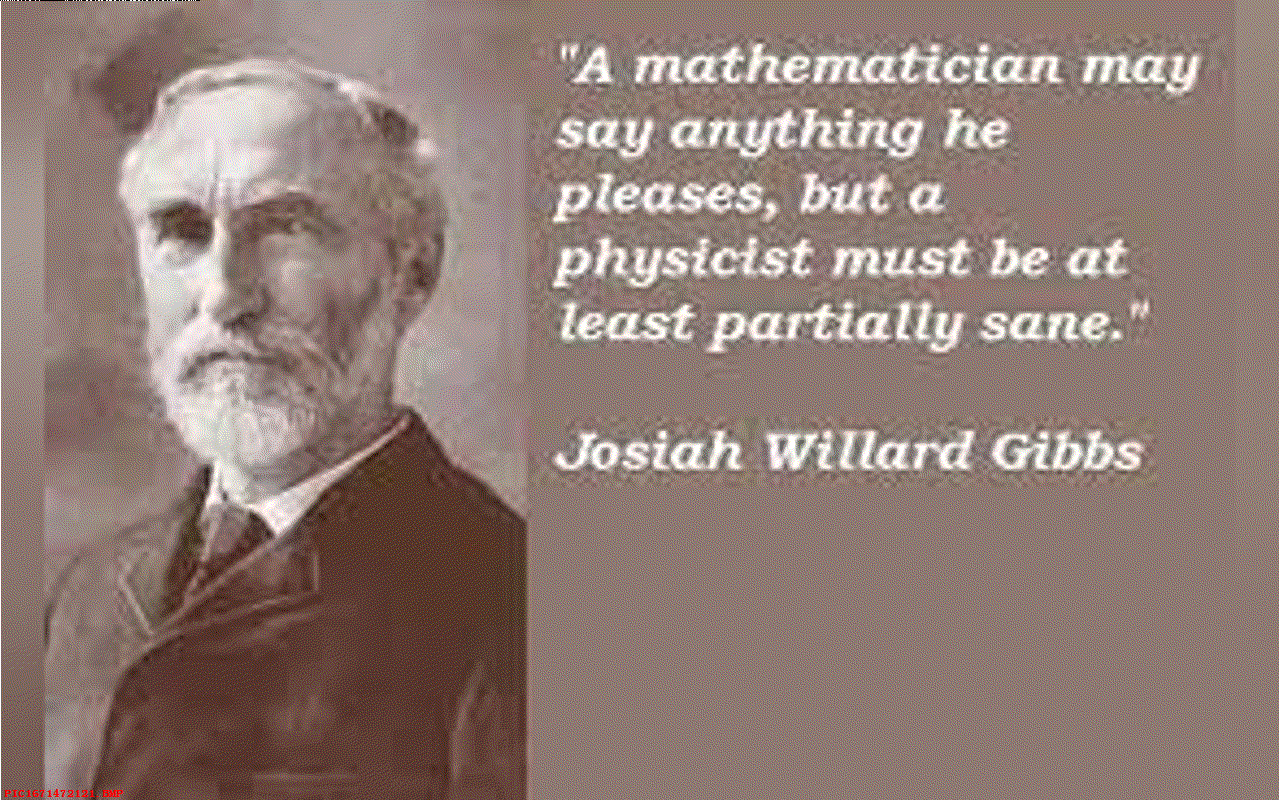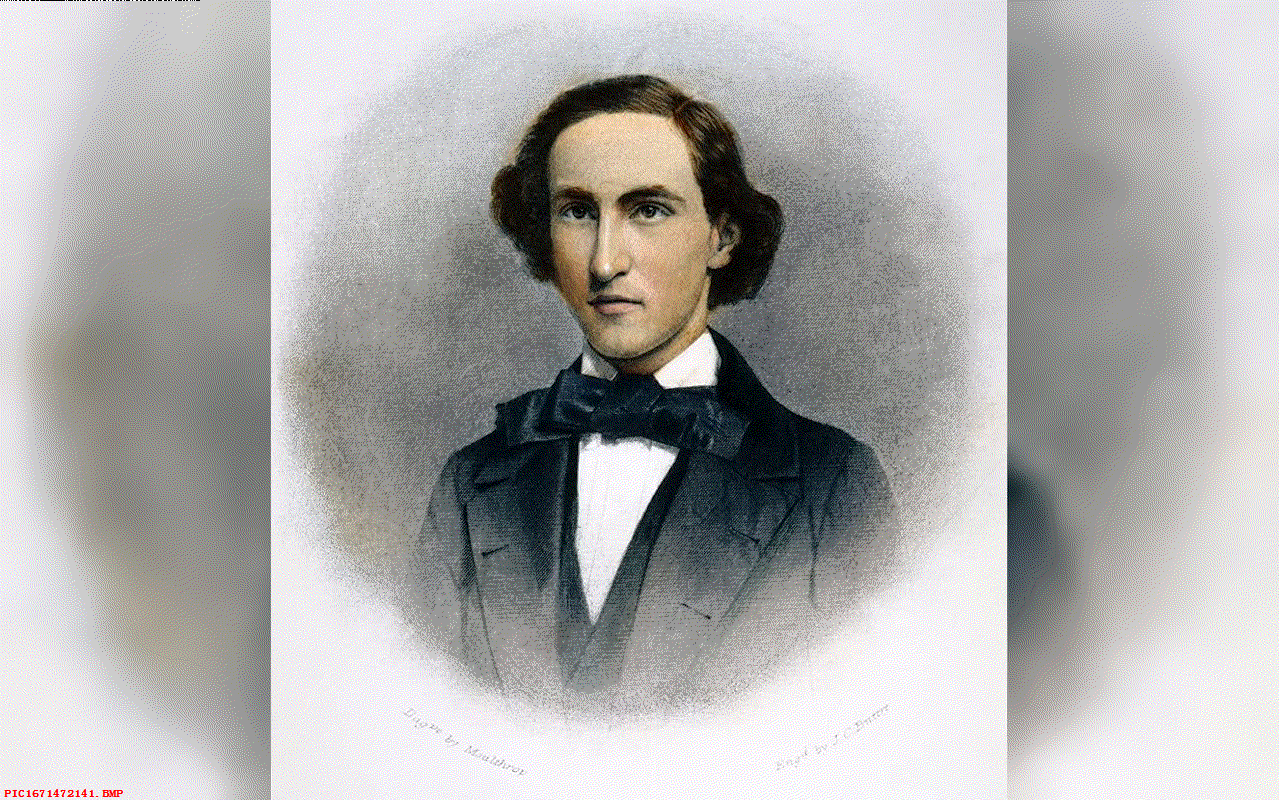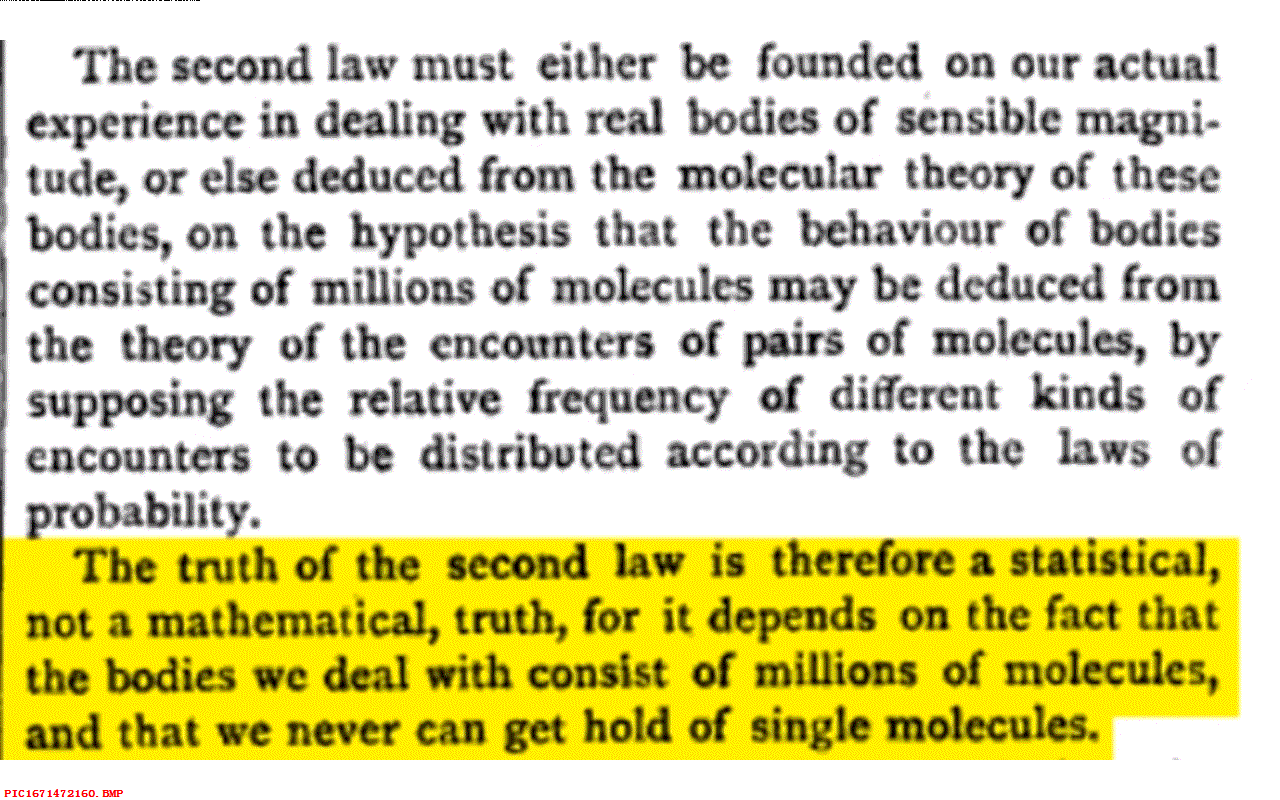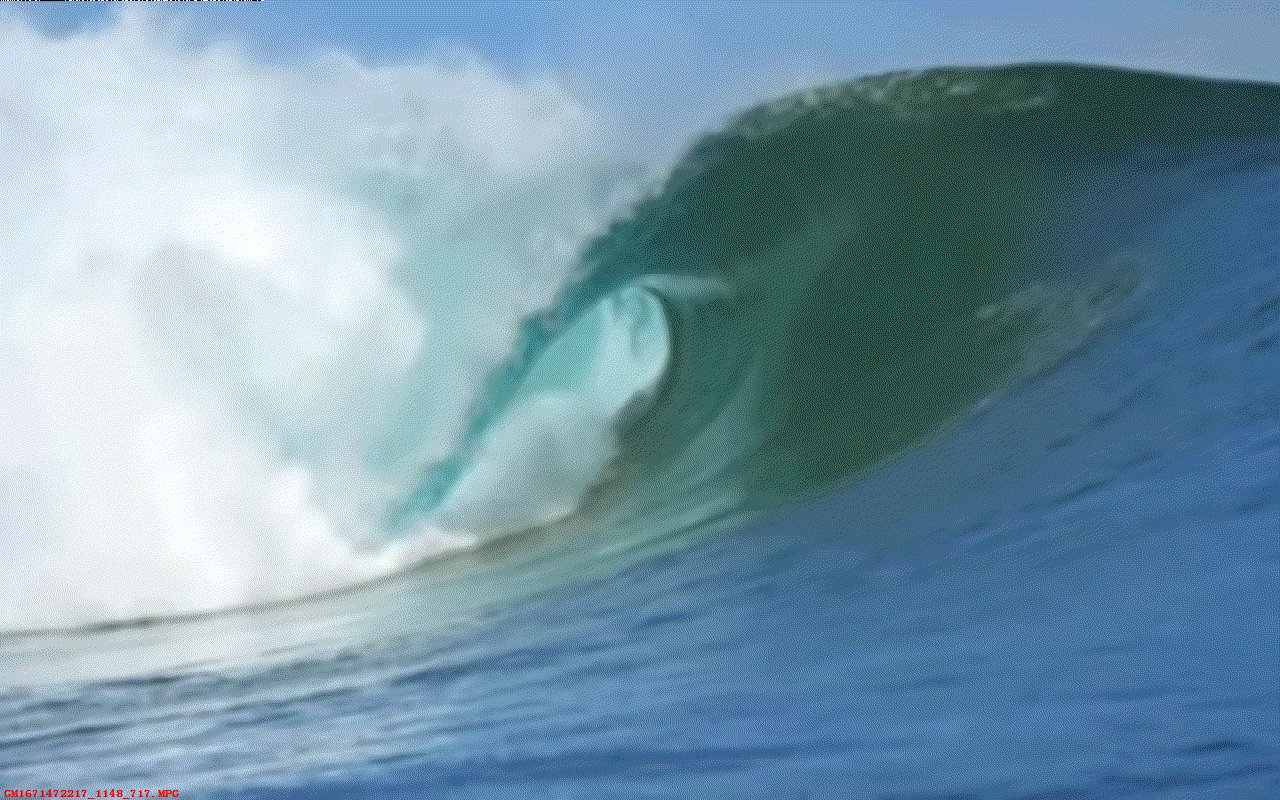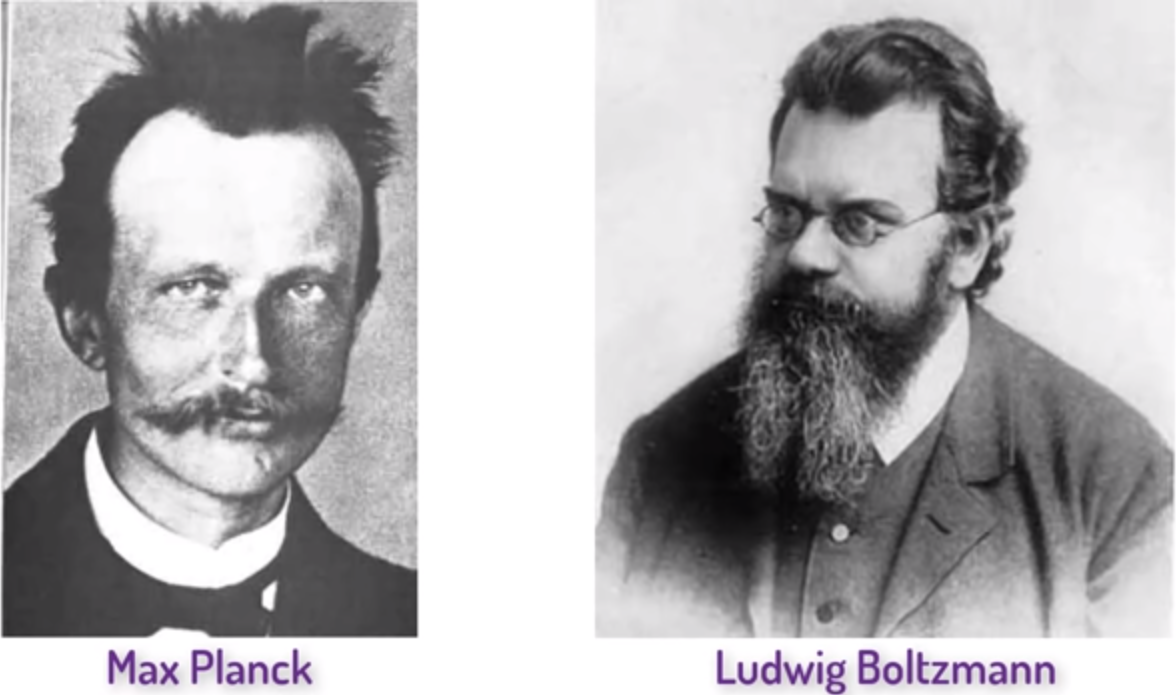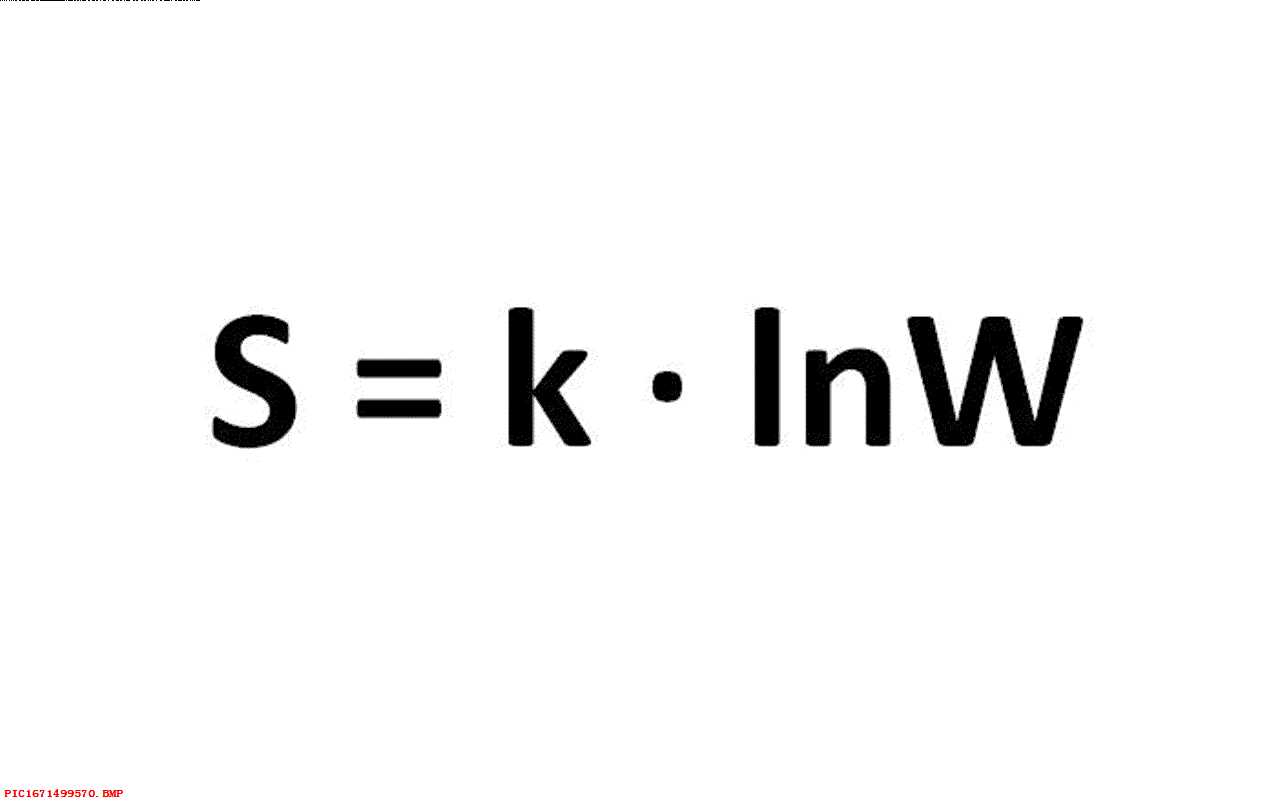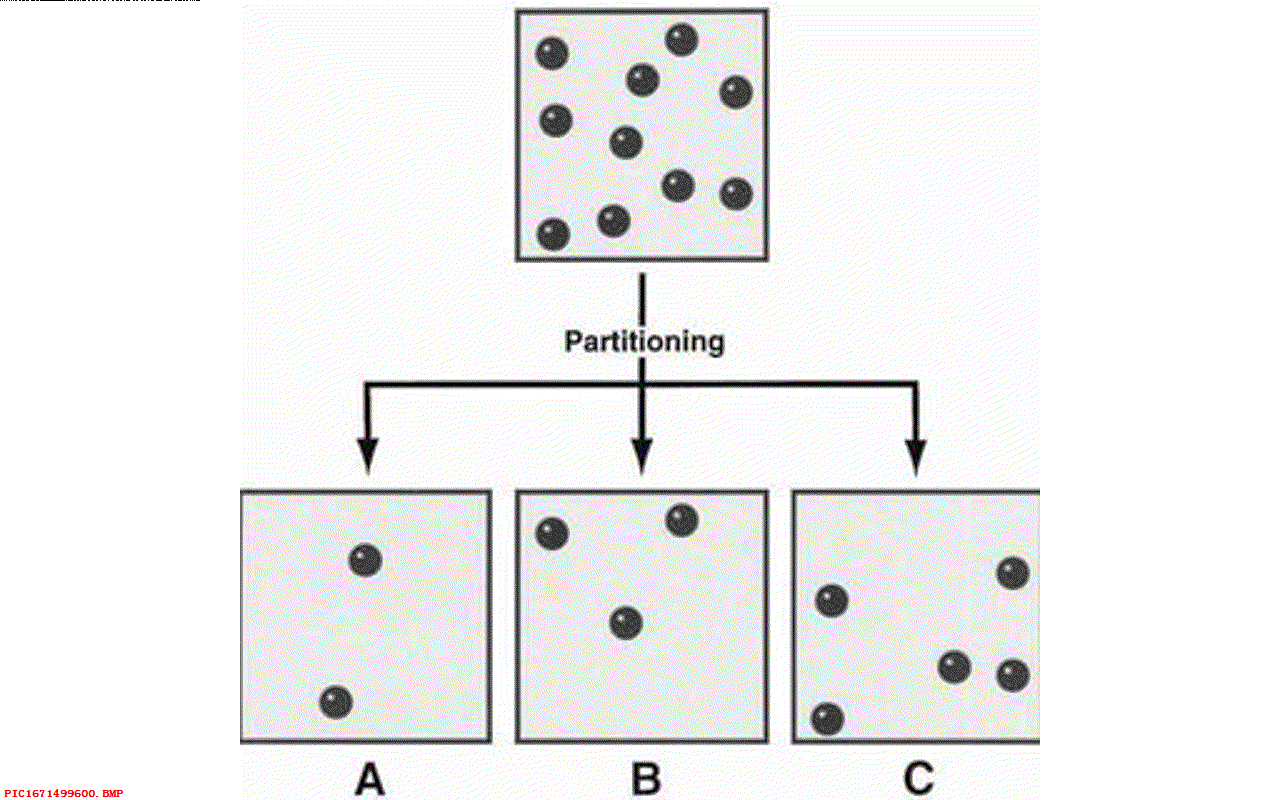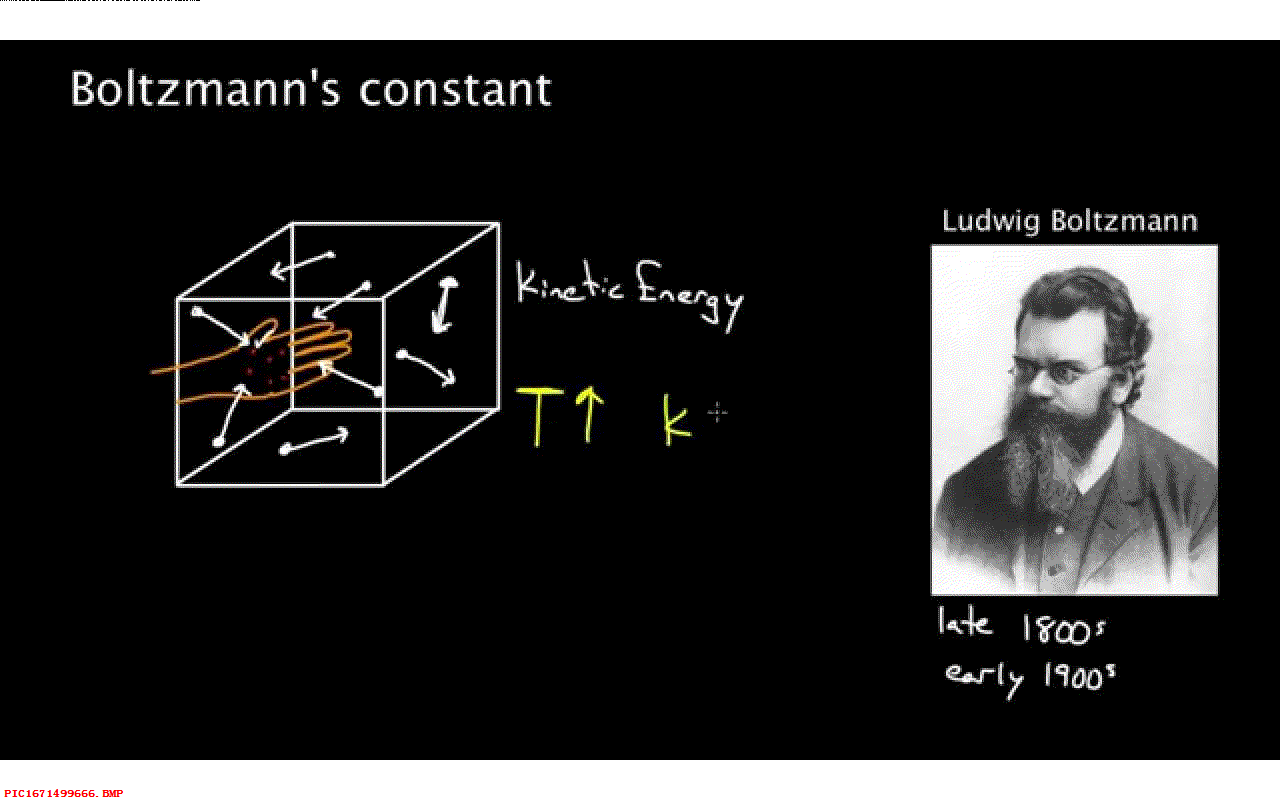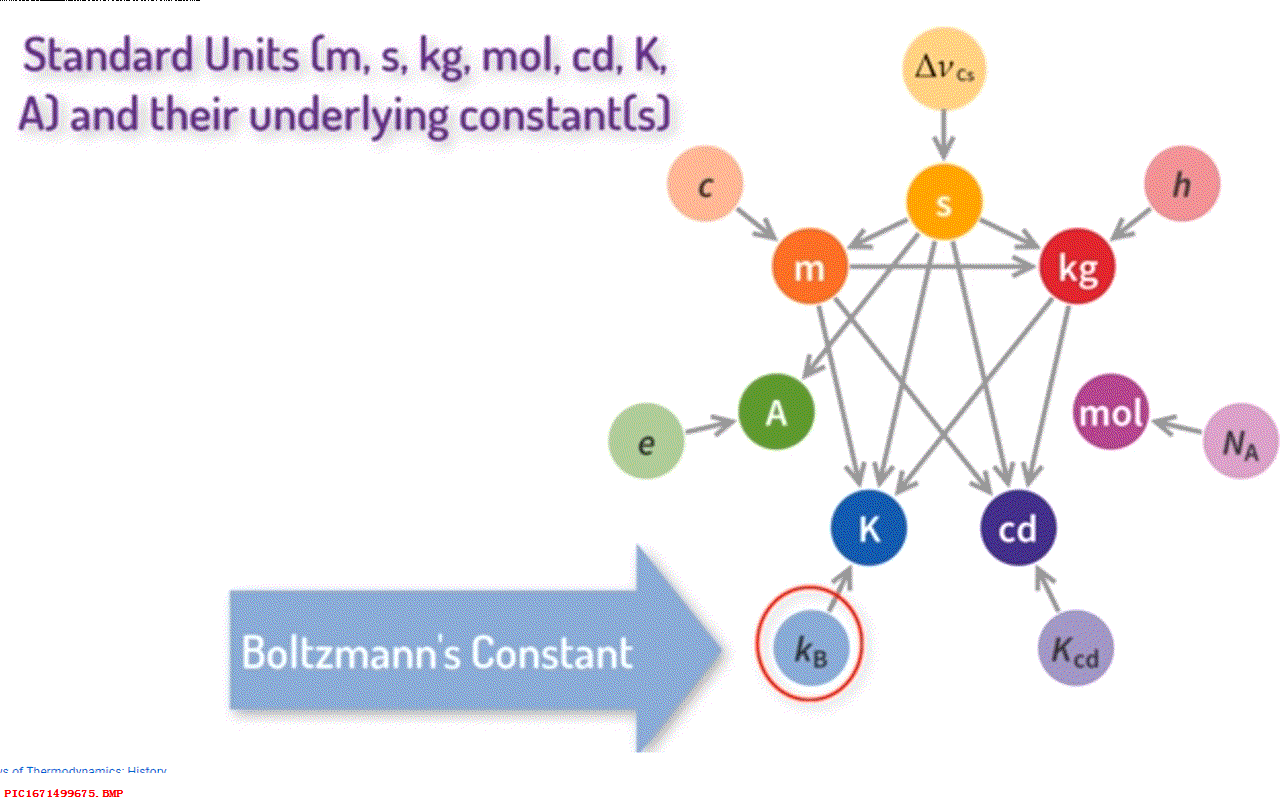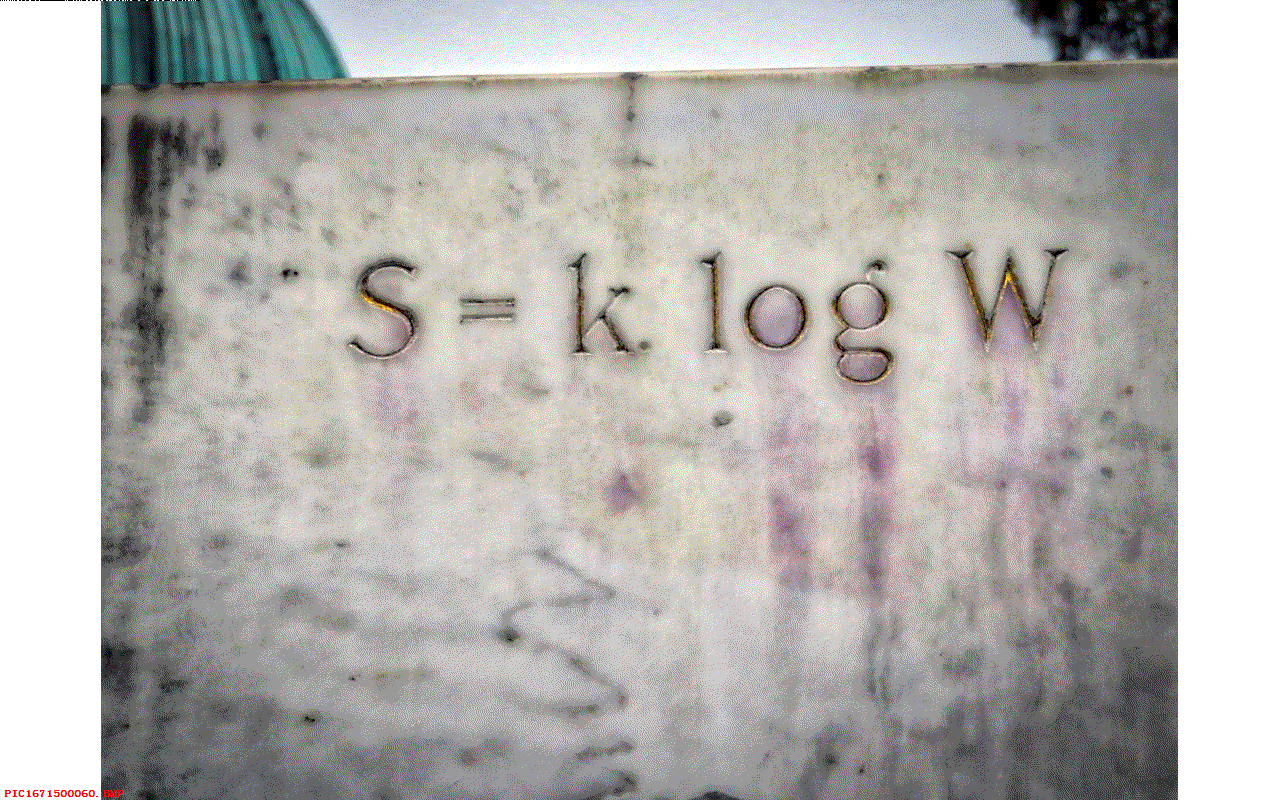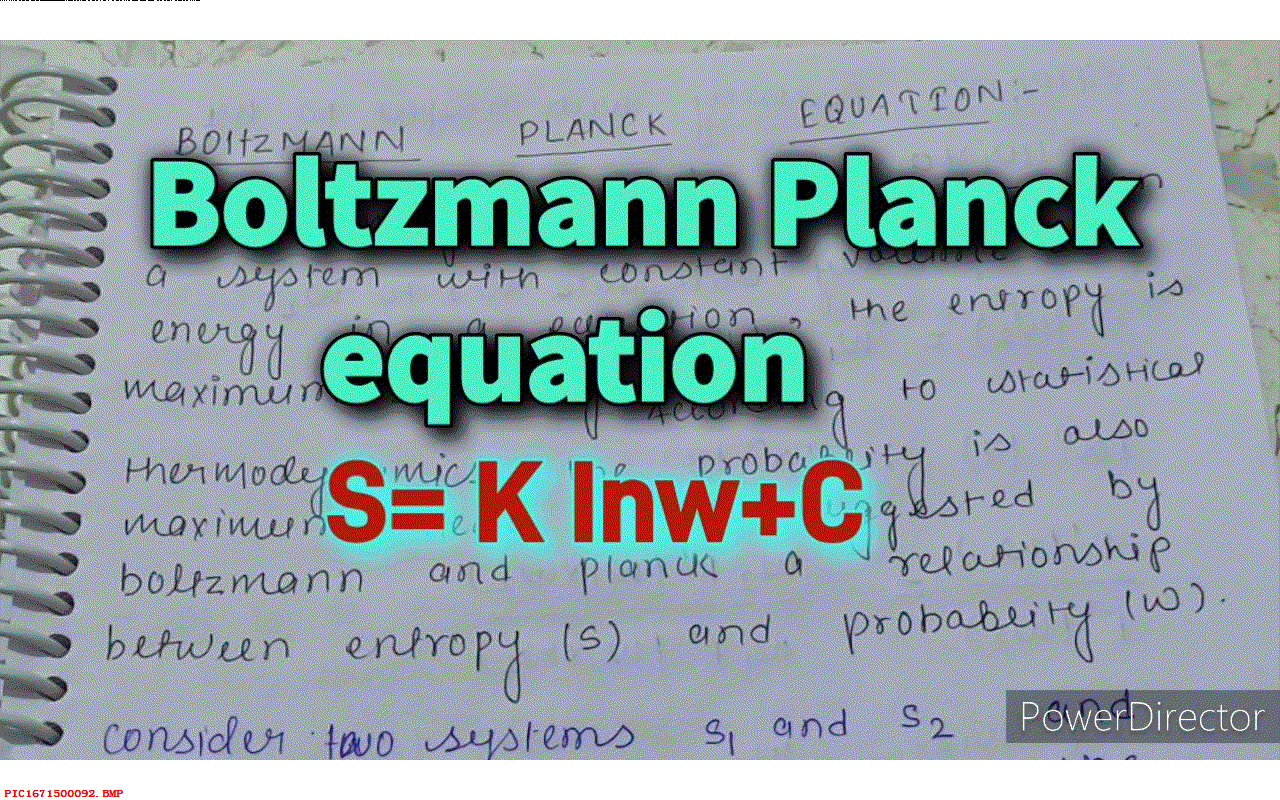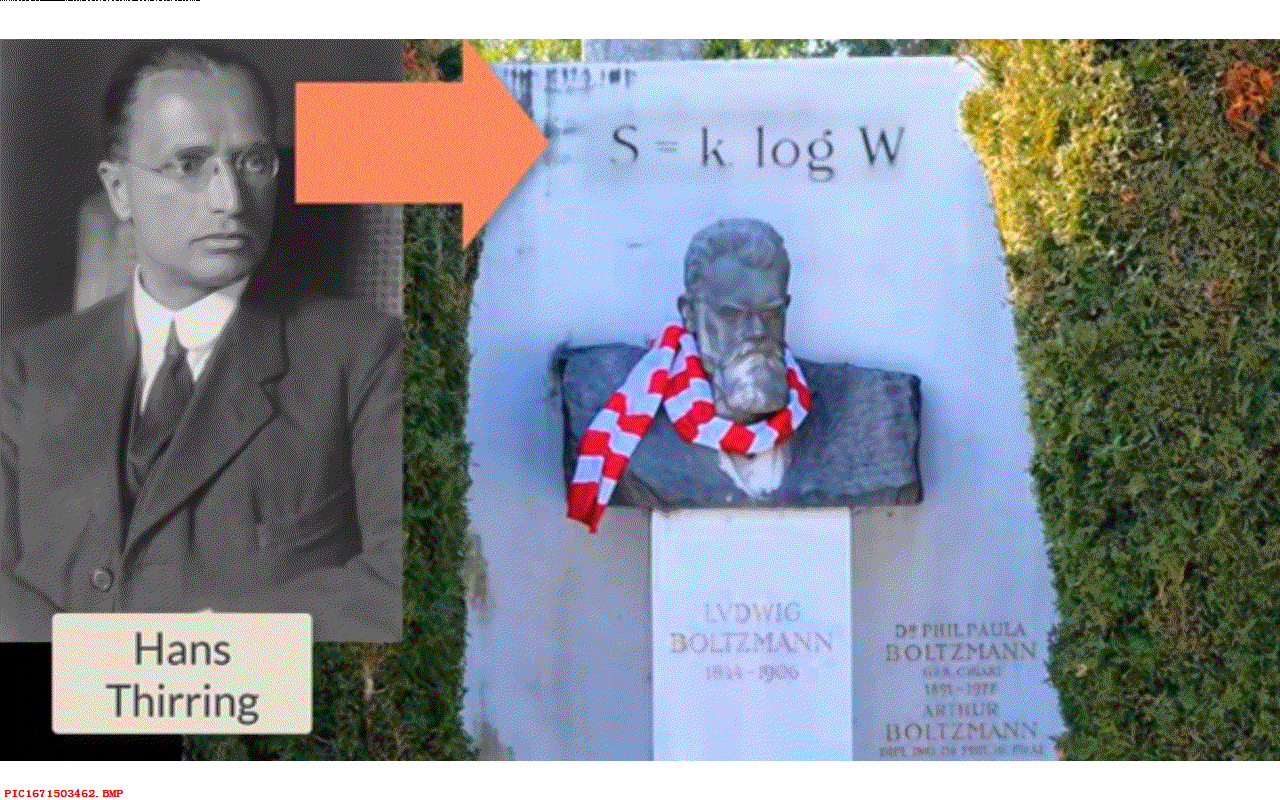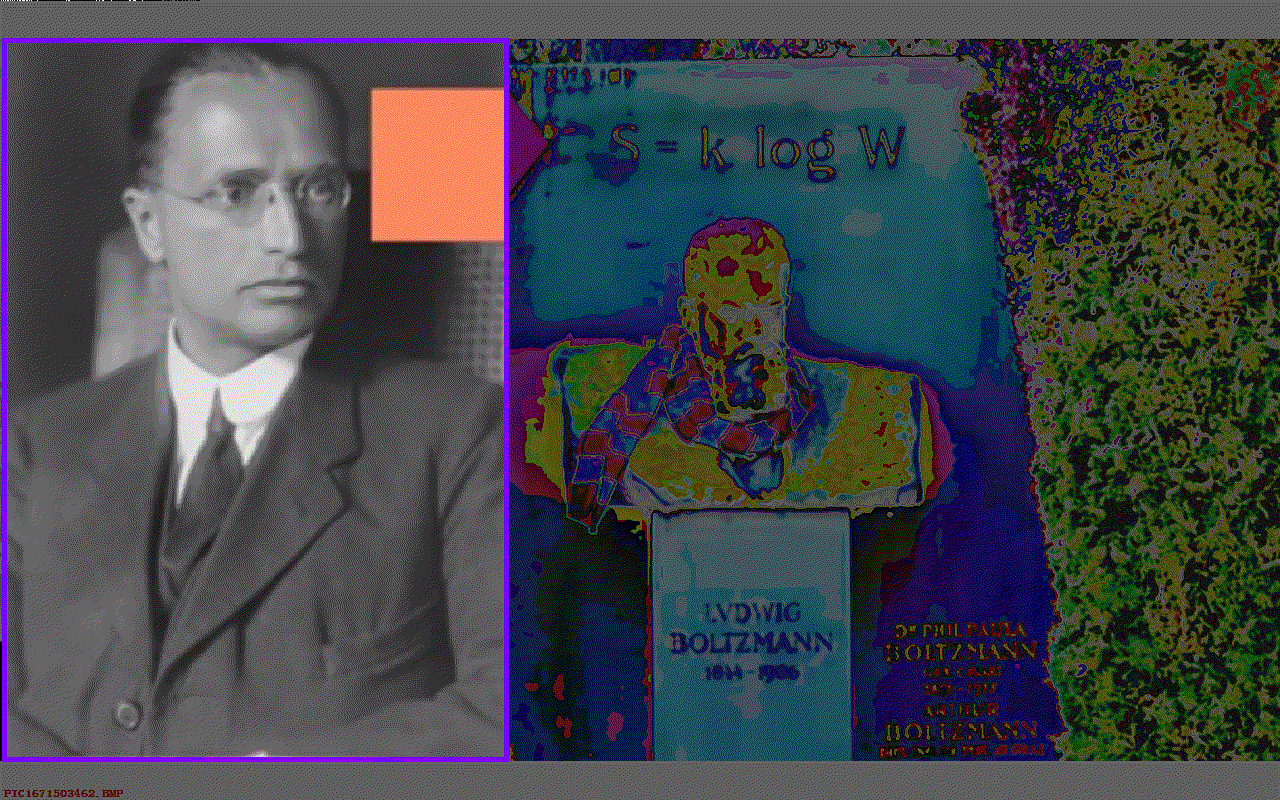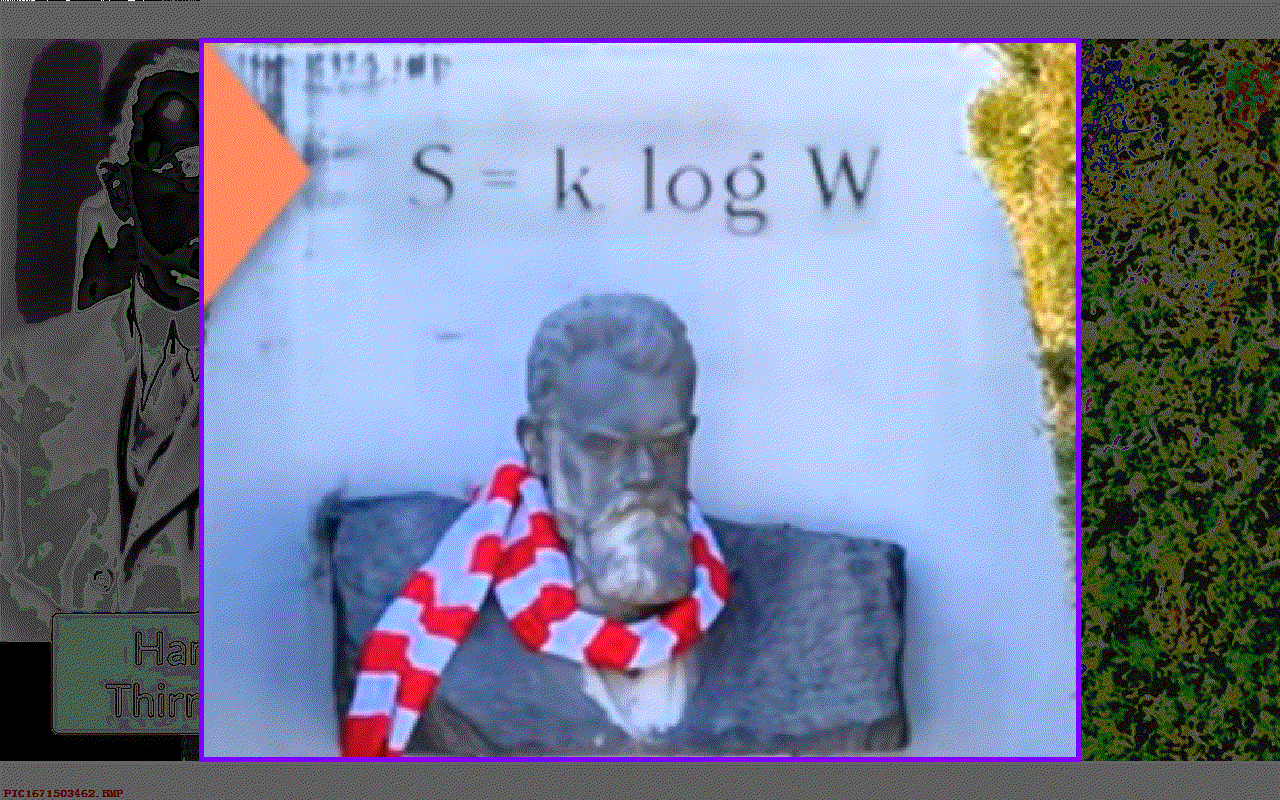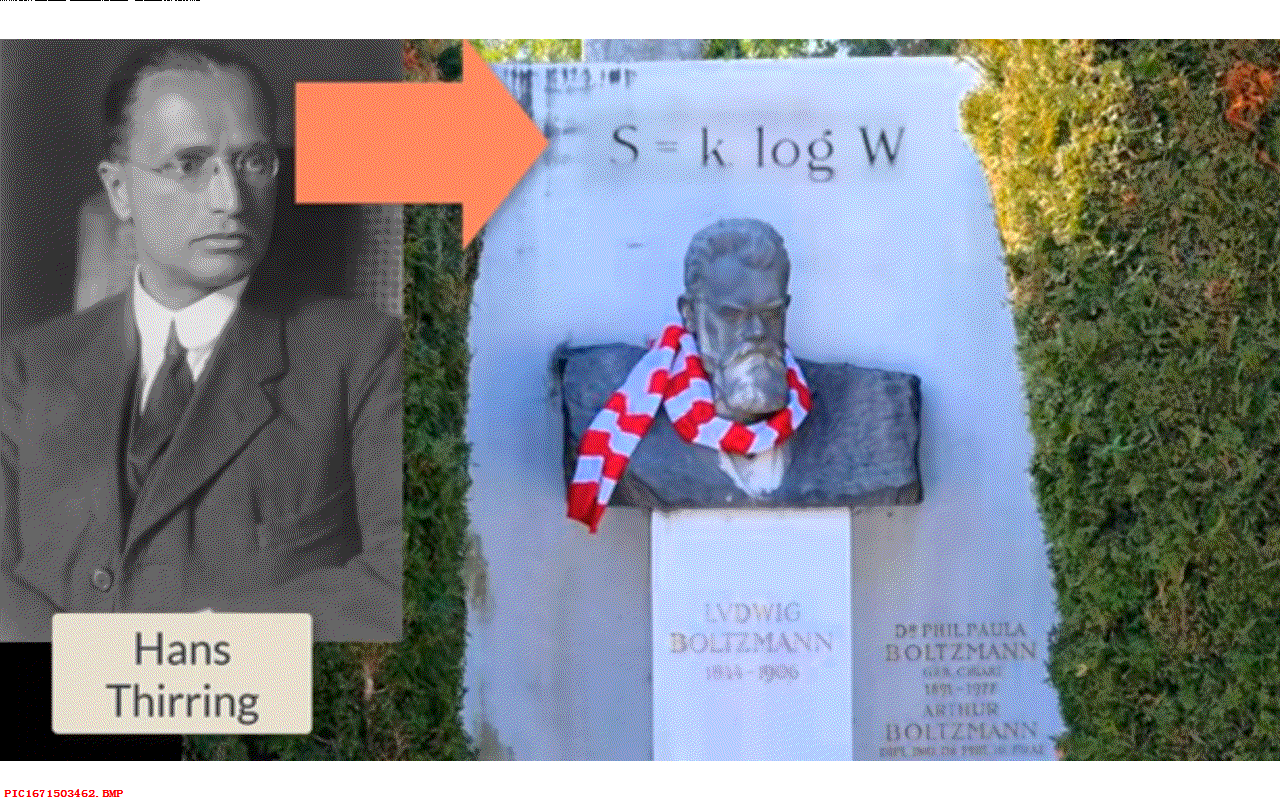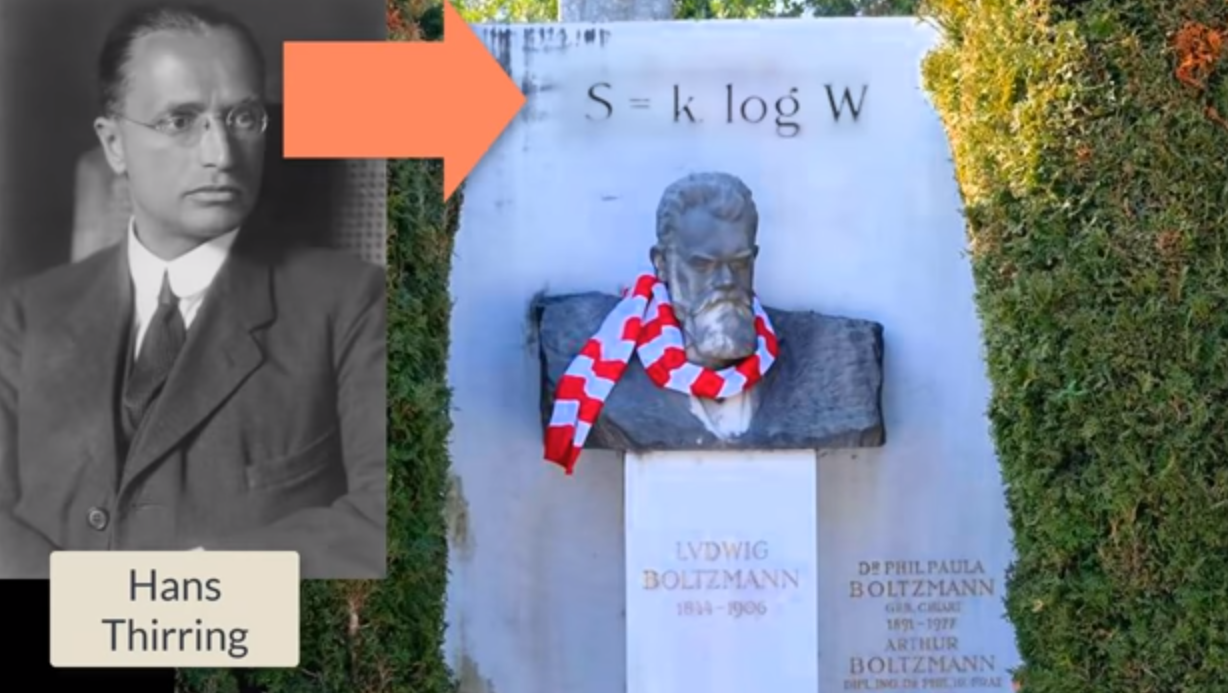玻尔兹曼熵公式 s=klnω_玻尔兹曼常数k与R的关系

• Boltzmanns Entropy Equation: A History from Clausius to Planck

玻尔兹曼熵等式最初是由马克思·普朗克在1900年创建的。那么为什么普朗克创见的这个等式却最终刻在了玻尔兹曼的墓碑上了呢？ Kathy老师利用最原始的资料来解释这个有名却令人困惑的方程。

01 Boltzmann熵等式

一、背景介绍

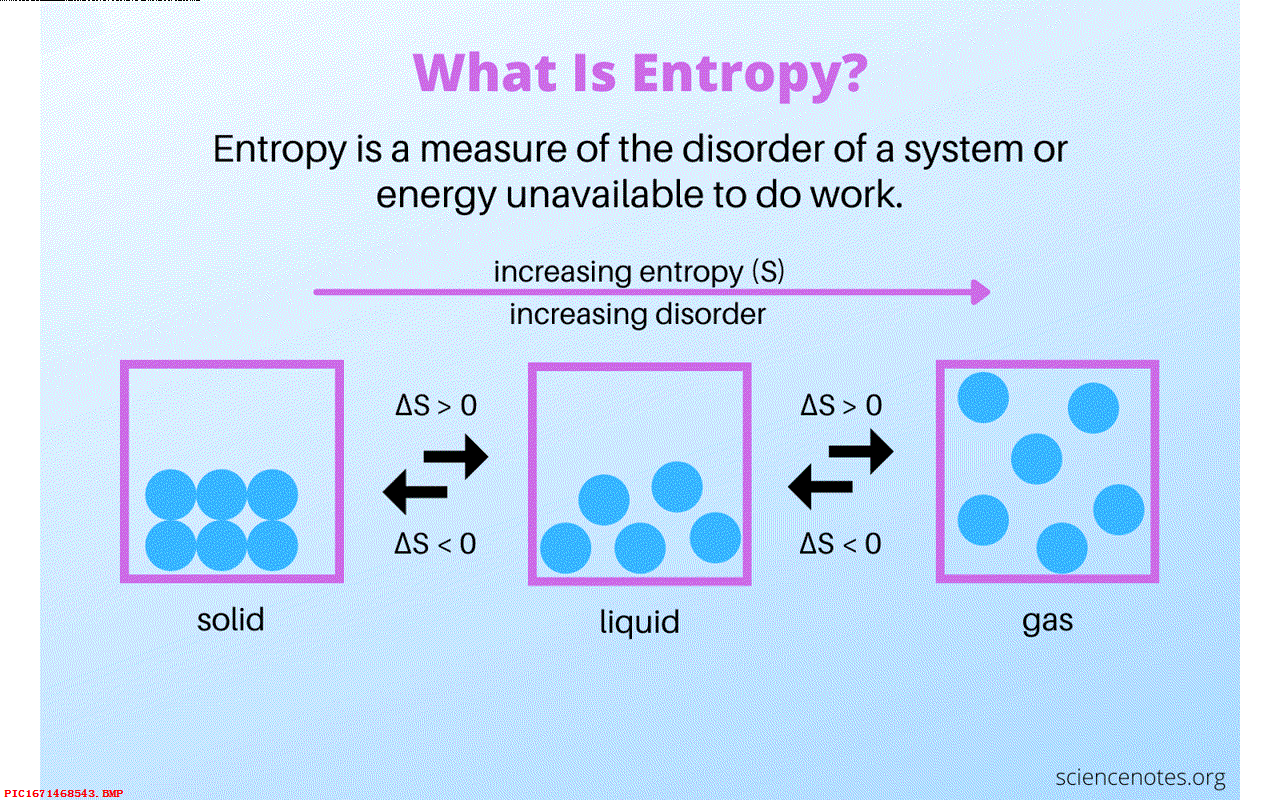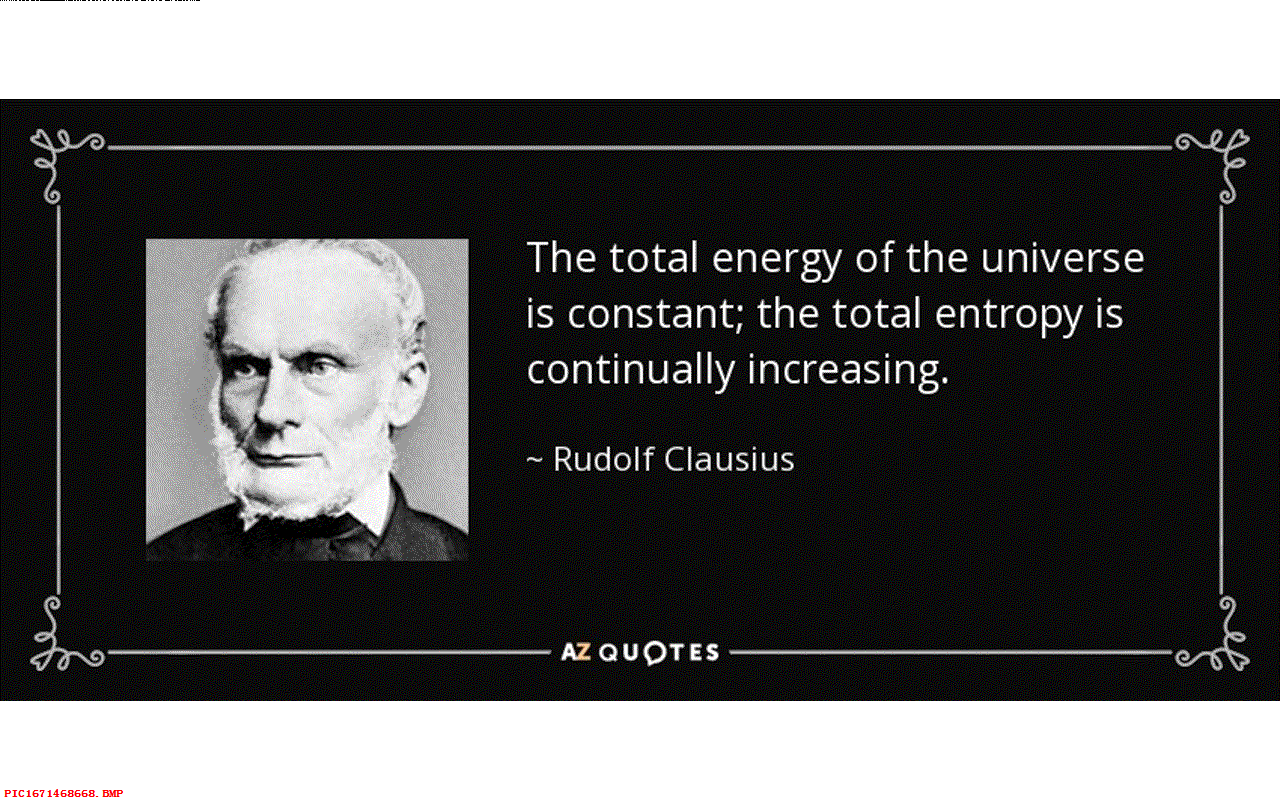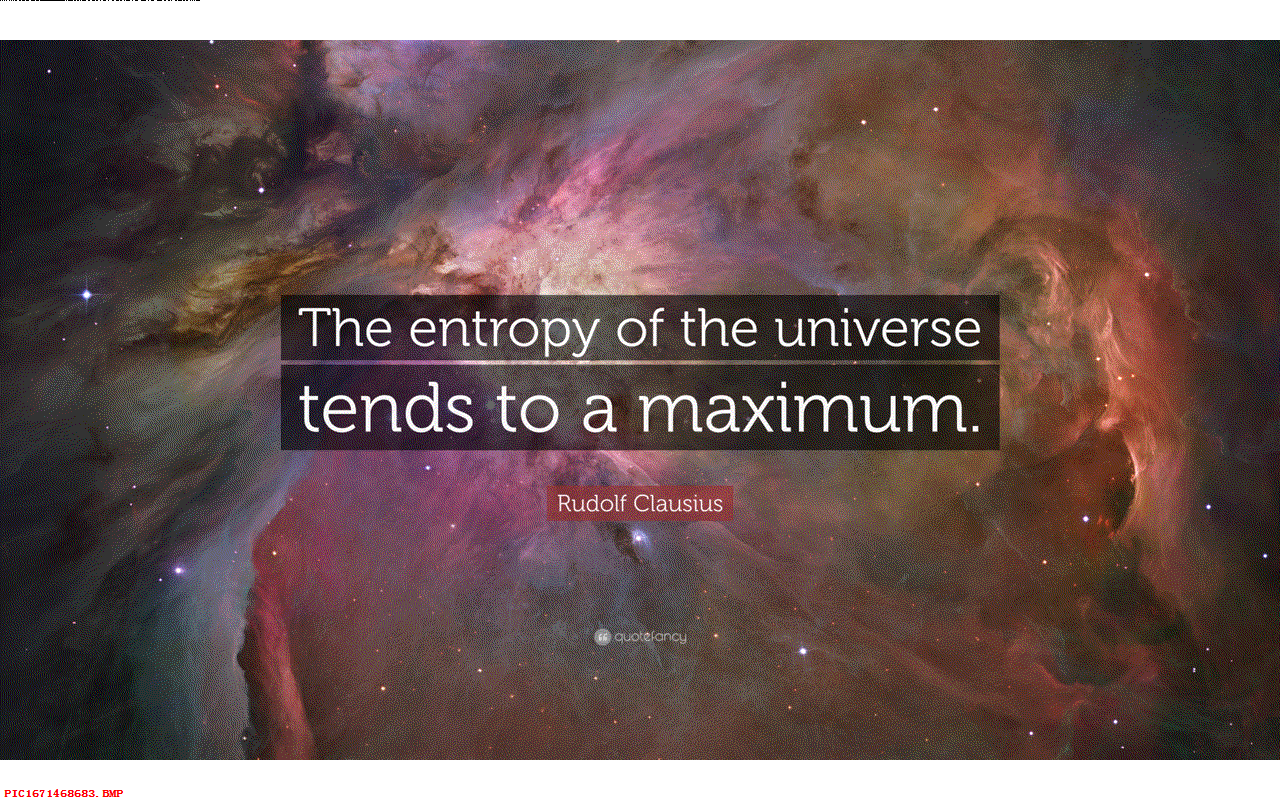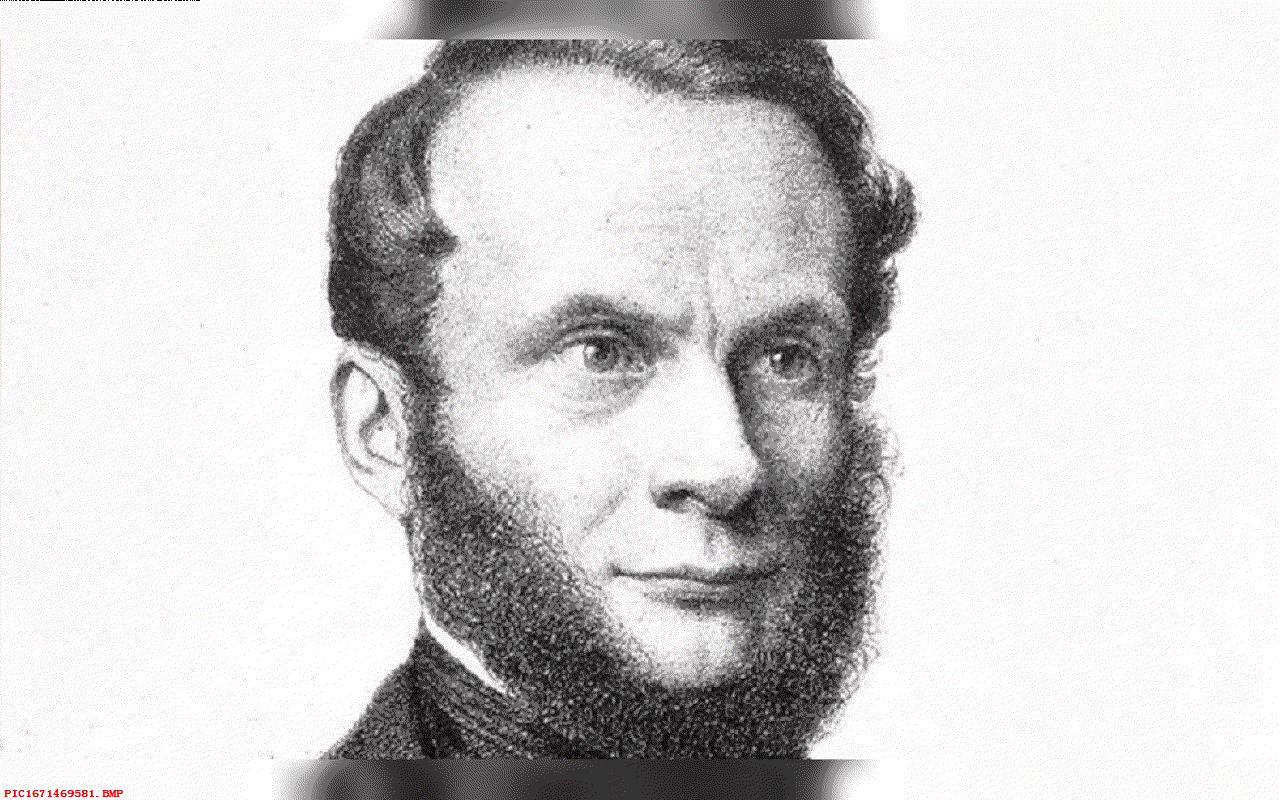
  玻尔兹曼熵公式也许是物理中所有公式中最难的方程了, 这并不是因为公式本身多么令人困惑，恰恰相反， 这个公式只有两个变量、一个常量以及对数函数。  两个变量分别代表了物理量熵， 以及不同能量状态的概率。 公式的困难来自于这两个大多数人难以理解的物理量。  所以我想透过历史迷雾去探寻这个公式是由谁写的？为什么写下这个公式？

  我发现这个公式是由马克思·普朗克在1900年创立的， 这与1901年的现代采用的公式几乎相同。 咦！等一等。为什么这个公式被人称为玻尔兹曼公式呢？ 公式中的常量被称为玻尔兹曼常数呢？ 要是普朗克首先提出了这个公式，为什么后来这个公式被刻在玻尔兹曼的墓碑上了呢？ 好吧，下面让我们听听Kathy老师来给我们解答这个疑问吧。

二、熵的起源

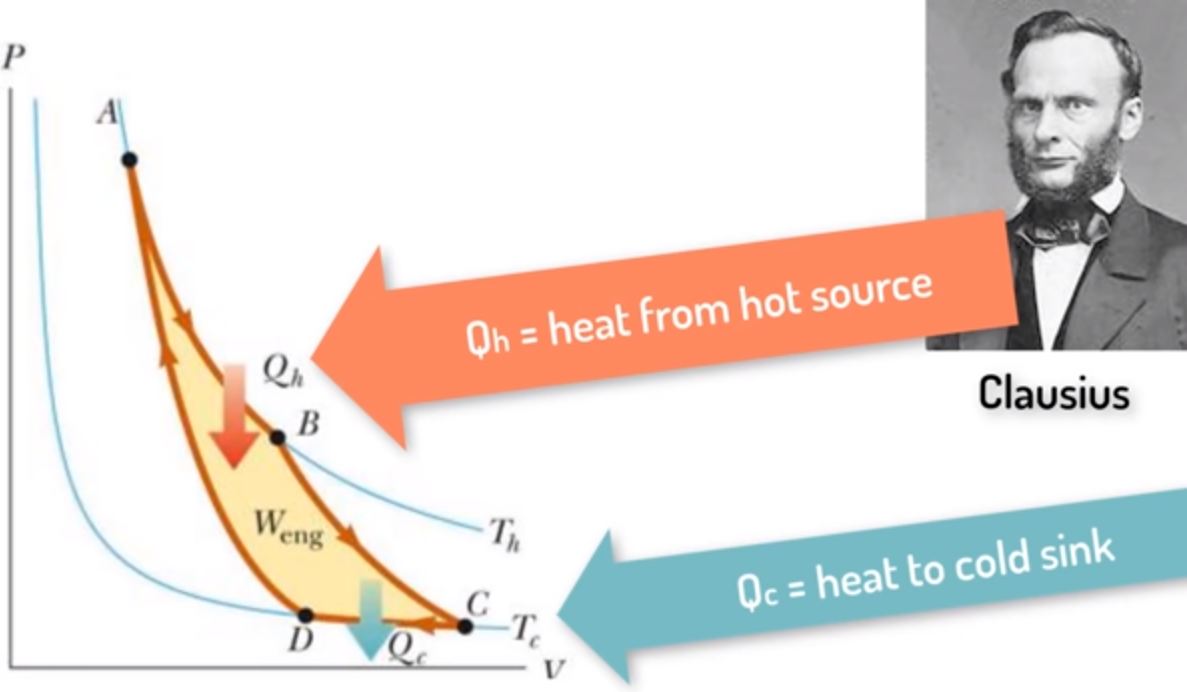
  首先让我们从关于熵的概念起源说起。 在1854年，一位德国科学家名叫鲁道夫·克劳修斯注意到物体在低温下所吸收少量的热量效果与在高温下吸收更多的热量的效果相同。 他于是将热量除以温度称为等效值，他后来称这个等效值为熵。 到了1862年，克劳修斯发现一个物体的熵的减少需要另外物体的熵的增加，因此任何封闭系统过程中总熵的变化大于等于0。 到了1865年克劳修斯把温度的等效值称为熵，使用字母 s 来表示， 并提出了热力学第二定律，也就是现在我们所说的宇宙的熵增定理。

  下面稍微花点时间介绍一下热力学中的概率的历史由来，这还得从德国人鲁道夫·克劳修斯谈起。 在1857年，克劳修斯第一篇介绍热量等效值论文发表后三年后， 克劳修斯撰文阐述温度反映了物体中分子的运动，也首先描述了物体分子的旋转、振动以及直线运形式， 即便有了很多限制，克劳修斯也发现物体分子运动的速度大的惊人。 比如，氢气分子在0摄氏度下运动速度居然超过五倍音速。

三、热扩散运动

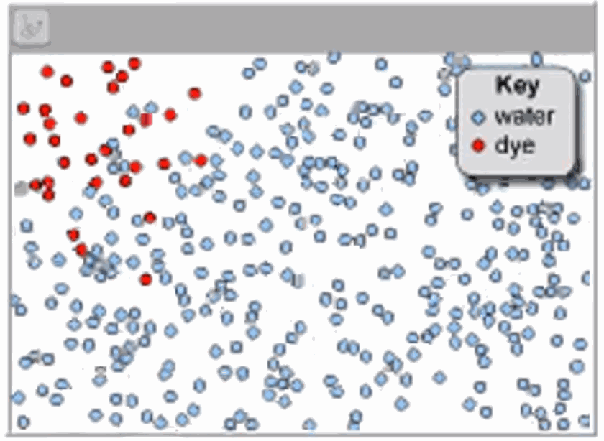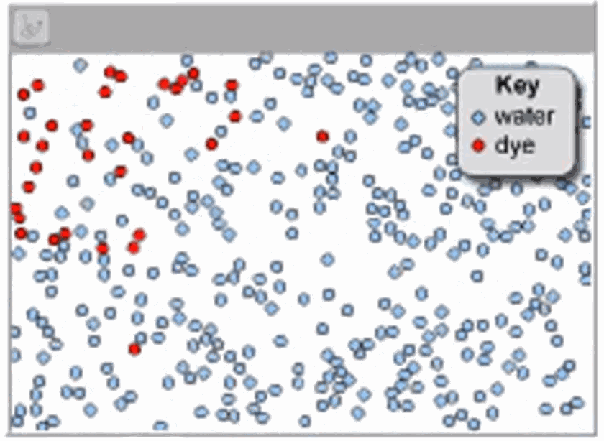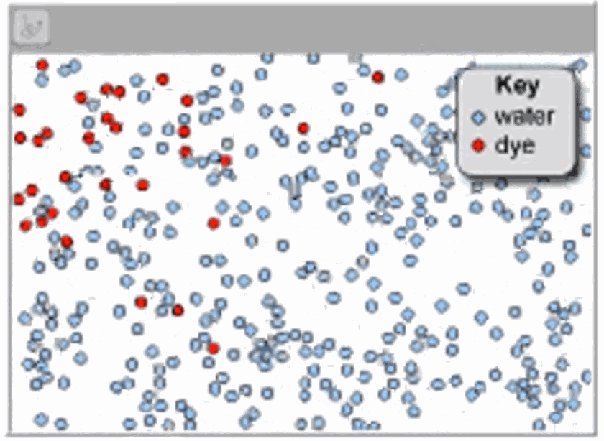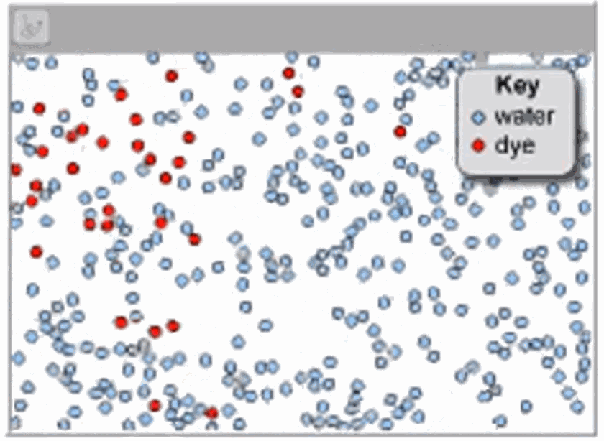
  读了克劳修斯论文之后，另外一位科学家发表论文进行反驳。 如果气体分子果真运动那么快，为啥香烟的烟雾并没有像声音那样快速充满整个房间呢？  克劳修斯认为这的确是一个有趣的反对意见，但并不说明他的理论错误，他也找到解释这个问题的方法。 气体分子运动的的确很快，但并不很远，这样就可以解释的很清楚了。 换句话说，在烟雾或者其它气体中存在着极其巨大数量的分子朝着各种方向运动，  但没有运动多长距离就碰到其它分子并改变方向，因此即便单个分子运动速度非常高，但气体本身扩散过程还是非常缓慢。 由此克劳修斯提出了一个新的概念，叫平均游程长度，即分子两次碰撞之间运动的平均距离长度。

  一位名叫弗雷德里克·格思里英国科学家，他是克劳修斯的粉丝，他掌握英语和德语两种语言， 他把克劳修斯的工作翻译成英语，在1859年2月发表。 三个月后，一位27岁的苏格兰科学家，名叫詹姆斯·克拉克·麦克斯韦在给一位朋友的信中写道， 克劳修斯的论文启发了他去测量分子的平均游程，方式是通过比较它与其它相关的现象。 从1860年到1866年，麦克斯韦发表了一系列的关于气体动力学理论的文章， 他承认正是因为克劳修斯的工作促使了气体动力学理论得以充分发展。 同一期间，麦克斯韦也发表了一系列关于电磁方面的论文，最终形成众所周知的麦克斯韦方程。

  1861年发生了一件有趣的事情，一天麦克斯韦困在人群中，迈克·法拉第在人群外冲他喊道， 吼吼，麦克斯韦你怎么困在人群里出不来了呀？ 别人不行，你应该是个例外呀。  显然法拉第这是暗指麦克斯韦在热力学统计方面的工作。

四、玻尔兹曼

  然而，如果说克劳修斯对于麦克斯韦的理论还是有点小意见的话，直到另外一位德国科学家，名叫路德维格·玻尔兹曼进入这个领域并参与其中。 玻尔兹曼比麦克斯韦年轻了13岁，他是1863年上大学，他的一位导师就非常欣赏玻尔兹曼的聪明。 据玻尔兹曼后来回忆道，他给我了一些麦克斯韦的论文， 说实在的那个时候我还不会英文，于是他又给我了一本英文语法书。 玻尔兹曼竭尽全力翻译阅读麦克斯韦论文很快并准备发表自己关于气体理论的论文， 三年后他便获得关于气体动力学方面的博士学位，那时他才25岁，并获得了全职教授职位。

  除了他那超人的智力，玻尔兹曼非同一般的教学能力也令其名声大振。 丽莎·迈特纳称他是其所见到的最好的老师，非常幽默，比如有一次玻尔兹曼说他数学一直很好， 只是在数自己喝完的啤酒杯的时候例外，这暗喻着实际情况。  他有时候会向动物学教授咨询如何去给母牛挤奶。

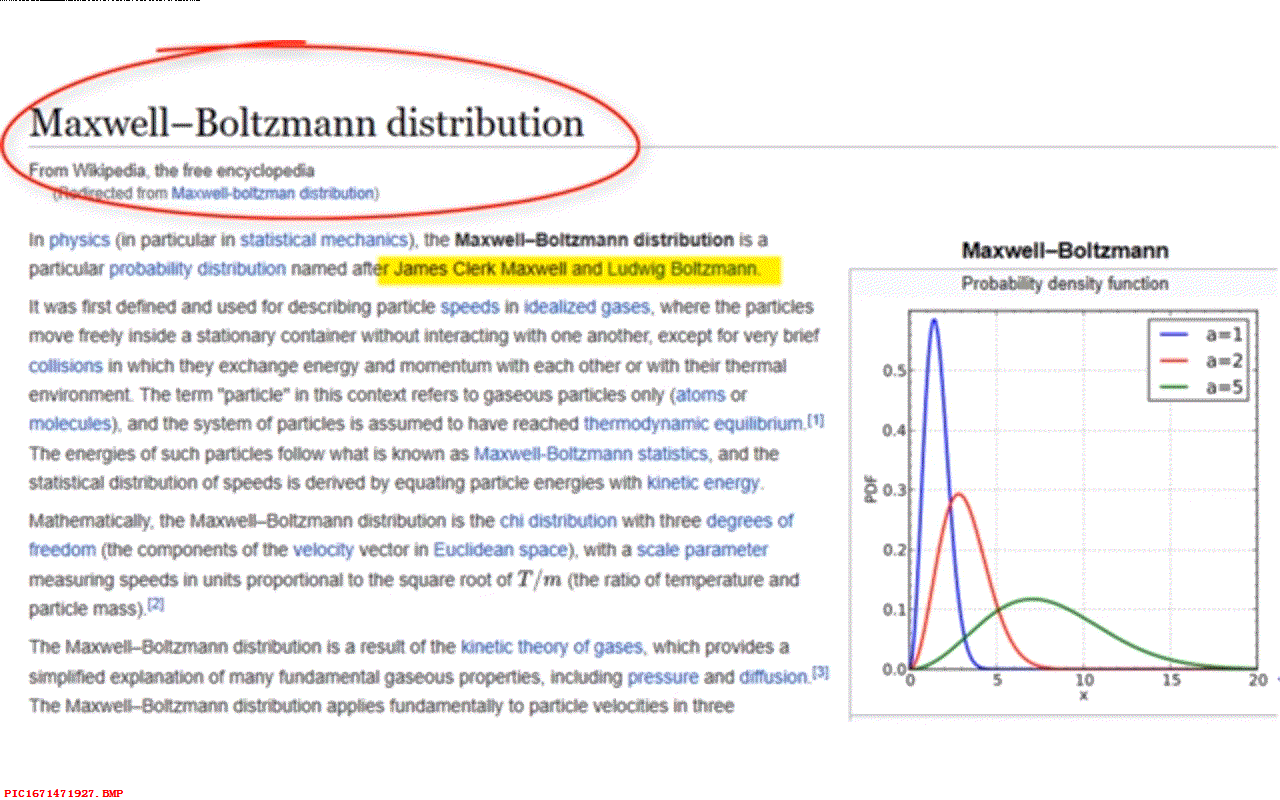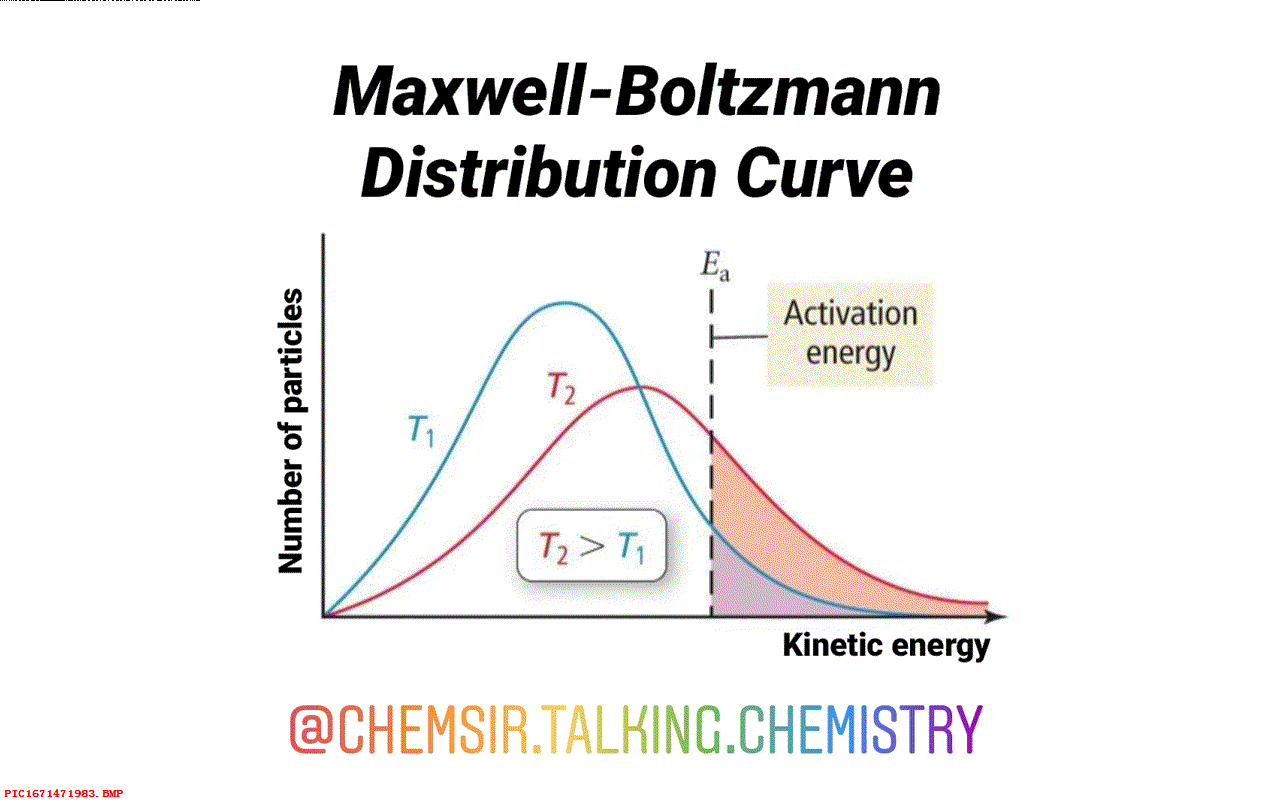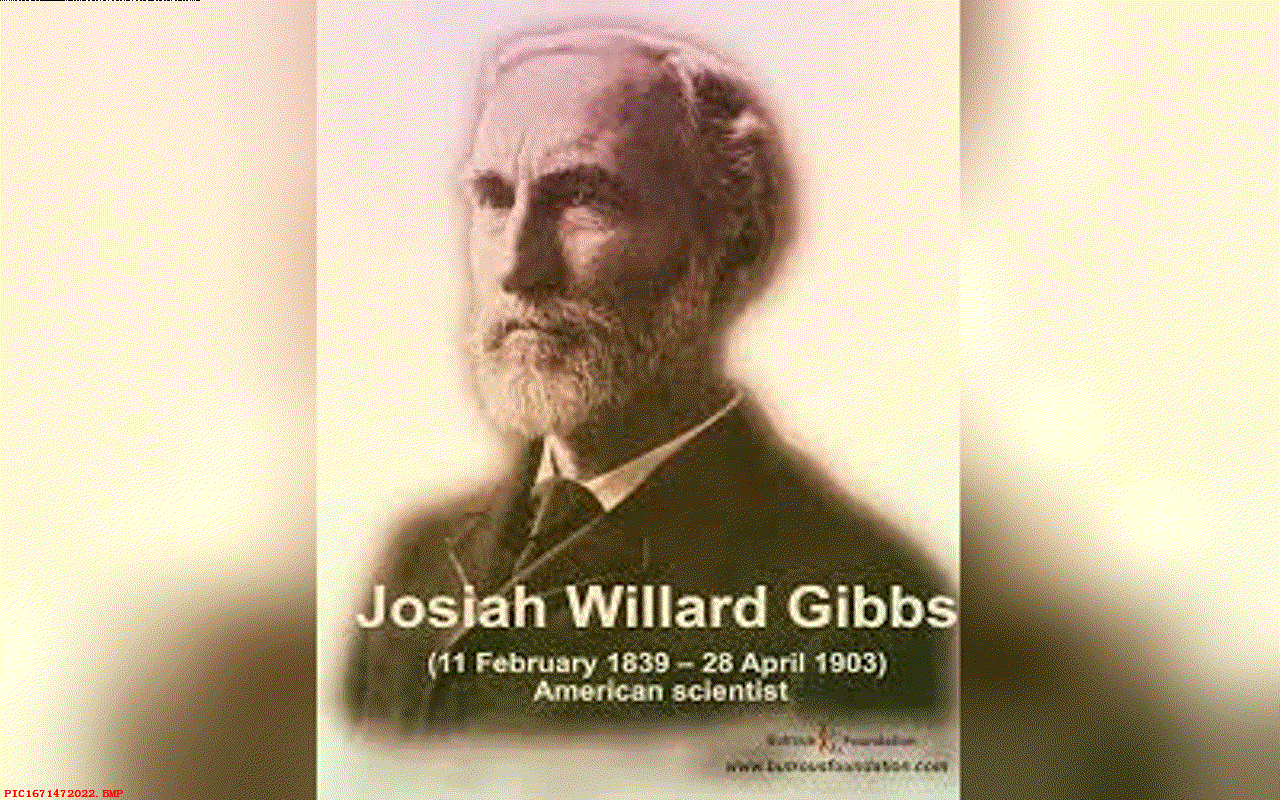
  麦克斯韦和玻尔兹曼关于热统计力学的研究，给出了麦克斯韦-玻尔兹曼分布， 即气体中不同速度的分子概率分布方程，这个分布被应用至今。 麦克斯韦开始倍感困惑的熵的概念，后来被一位名叫约西亚·吉布斯的美国人给澄清了，他使用自己关于分子统计研究中的方法来研究熵。

  吉布斯的工作让麦克斯韦确定热力学第二定律真实含义是统计意义上的，而不是数学真理。 这是因为它涉及到由成千上万无数分子组成的物体，我们无法确定其中单个分子的状态。 正像麦克斯韦给朋友所做的有趣的比喻。 热动力学定律所描述的正如我们把一杯水倒入大海之后，你再也无法将它们取出组成相同的一杯水了。

  谁知高傲的克劳修斯对于麦克斯韦把他的热力学定律贬低到如此浅显很不满意，但他的确遇到了大麻烦。 第一个麻烦是1870年，克劳修斯参加了俄法战争，他在组织救护队的时候受伤了。 第二个麻烦是五年后，1875年，克劳修斯的老婆在生孩子的时候不幸去世。克劳修斯不得不放下研究工作，一边教学一边抚养他的六个孩子。 克劳修斯直到临近去世还在从事教学工作。

五、玻尔兹曼与熵

  年轻的玻尔兹曼在麦克斯韦的鼓动下开始研究统计学与熵的关系。 早在1872年，玻尔兹曼写到，物体中的分子数量是如此之多，运动如此之快，我们只能感知它们的平均值，因此关于热的动力学问题就是概率论的问题。 从1877年开始，玻尔兹曼便投身研究概率统计与熵之间的关系。他先从一个关于纸牌游戏的概念开始思考， 对于任何随机的五张牌恰好是1,2,3,4,5的可能性非常小，这是因为随着时间演化均匀分布的可能性比起任何特殊分布要多的多。  人们可以计算出不同状态的相对数量。

  1877年十月，玻尔兹曼给出了计算这种分布的公式， 最终给出了一篇充满公式的50页的论文（至今还是没有被翻译的德文）， 论文中他将分子的能量分割成不同的间隔，对于不同情况分别进行了讨论。 论文中他写到，将这些数学分析方法应用到第二定律，我们可以获得通常被称为熵的数量，就是不同问题中不同状态的概率。 然后玻尔兹曼并没有将与概率相关的熵的公式与这个新的定义的概率联系起来。

  另外感到惊讶的是，麦克斯韦与玻尔兹曼两个人都从他们各自长着科学脑袋的老婆那里获得了帮助。 凯瑟琳·麦克斯韦并没有受过科学和数学方面的训练，但记录表明她在实验方面给了她丈夫以帮助。 实际上，在1877年麦克斯韦的一个朋友给他写信索要流体粘度方面的数据， 他回信到，我的天生绝配的另外一半帮我做了所有关于动力理论方面的实际工作，不过现在她在忙别的研究工作。当她闲下来我就会让你得到想要的答案了。

  玻尔兹曼的老婆也不是吃素的，名叫恒瑞特·玻尔兹曼，在她上中学的时候就想学习物理和数学了。 甚至在玻尔兹曼的建议下想方设法去旁听一些课程。 甚至在求婚的时候，玻尔兹曼称她为数学家，并称对我来说，如果妻子对于丈夫的努力不理解和痴迷，爱情无法持久。他们只是生活中的朋友，并不能共同奋斗。 恒瑞特不仅需要忙于照顾五个孩子，还需要处理玻尔兹曼低落的情绪。

  麦克斯韦和玻尔兹曼共同工作了许多年。 到了1877春天詹姆斯·克拉克·麦克斯韦病倒了， 并在两年后，1879年11月因胃癌去世，年仅48岁。 恒瑞特、路德维格·玻尔兹曼继续发表关于统计、热学、概率、以及熵方面的论文。然而他们越来越感到在德国被孤立起来了。 因为分子的存在在当时还是相当前卫的概念，在已存在的物理架构中并不流行。

六、普朗克

  现在我们反过头来介绍一下马克思·普朗克。普朗克比玻尔兹曼年轻14岁。 在1877年，也就是麦克斯韦病倒的那一年，玻尔兹曼发表了关于概率的长文。 普朗克来到研究生院，发现那里所有的研究者教授的课程都非常差，这令他感到非常沮丧，他决定自己阅读论文原文。 过了几年，他后来回忆道，一天我偶然阅读了鲁道夫·克劳修斯的论文，立即就被论文的流畅的写作风格、清晰的推理过程深深吸引，随着对论文的阅读的深入我越来越激情澎湃，非常欣赏书中对于热动力学第二定律清晰的公式描述。

  两年后，1879年普朗克获得了他的博士学位，研究内容就是热力学第二定律。 不过他认为在他研究的日子里没有一个物理学家对他产生了影响，并对论文内容有所了解。 即使最相近领域的研究人员对于答辩毫无兴趣。 甚至克劳修斯也对他的论文毫不关心，普朗克去他的房间拜访过好几次都毫无回应。

  尽快如此，1889年马克思·普朗克还是设法在柏林大学获得了教授职位。 普朗克于是和被称为能量学派的学者卷入了一场争论。 能量学派相信能量，而不是熵，不承认分子理论，也不赞同使用绝对零度作为温度测量基准。 在争论中，普朗克发现一个奇怪的理论的守护者，名叫路德维格·玻尔兹曼。 在1896年，玻尔兹曼还将与能量学派的争论进行了发表， 争论内容是对于年青一代来说关于热力学第二定律的有效性哪一种观点更方便呢？ 年轻气盛的普朗克也觉得这个玻尔兹曼也顺带攻击了他。普朗克从来都不喜欢玻尔兹曼的统计理论，他曾说到，我认为熵增定律并不像能量守恒那样普遍适用。 玻尔兹曼把前者当做概率定理，所以在他后来研究原子的整个过程中的玻尔兹曼对其都漠不关心甚至有些敌意。

七、普朗克与熵

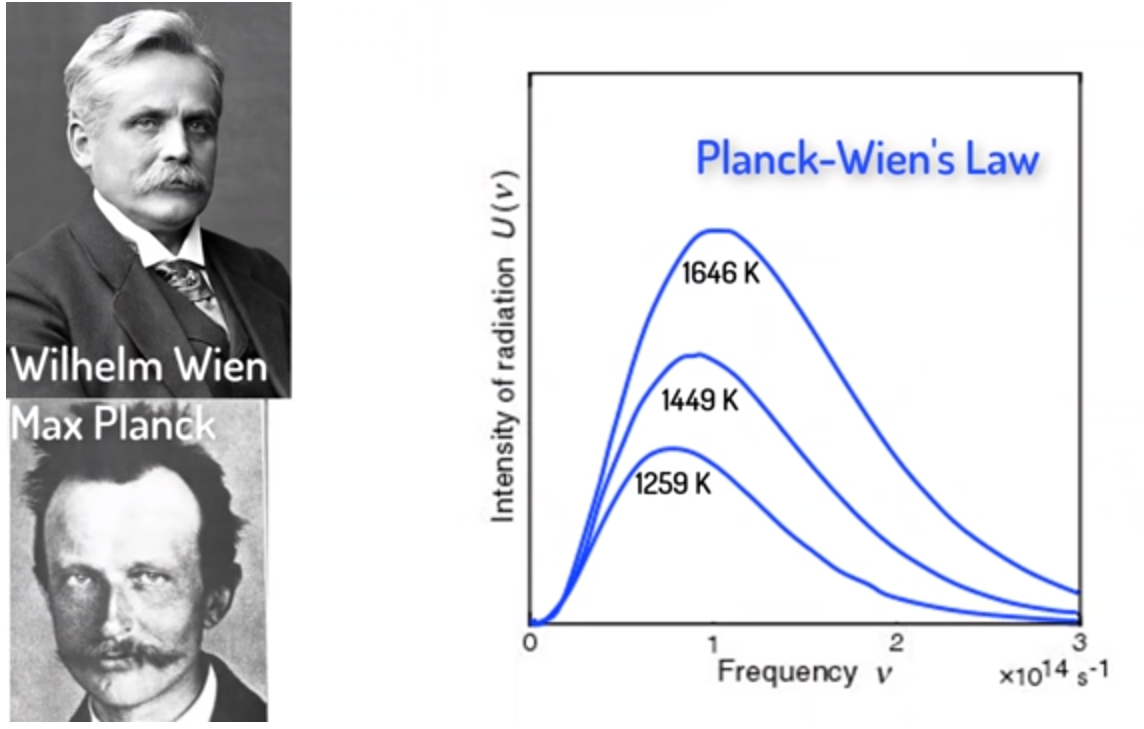
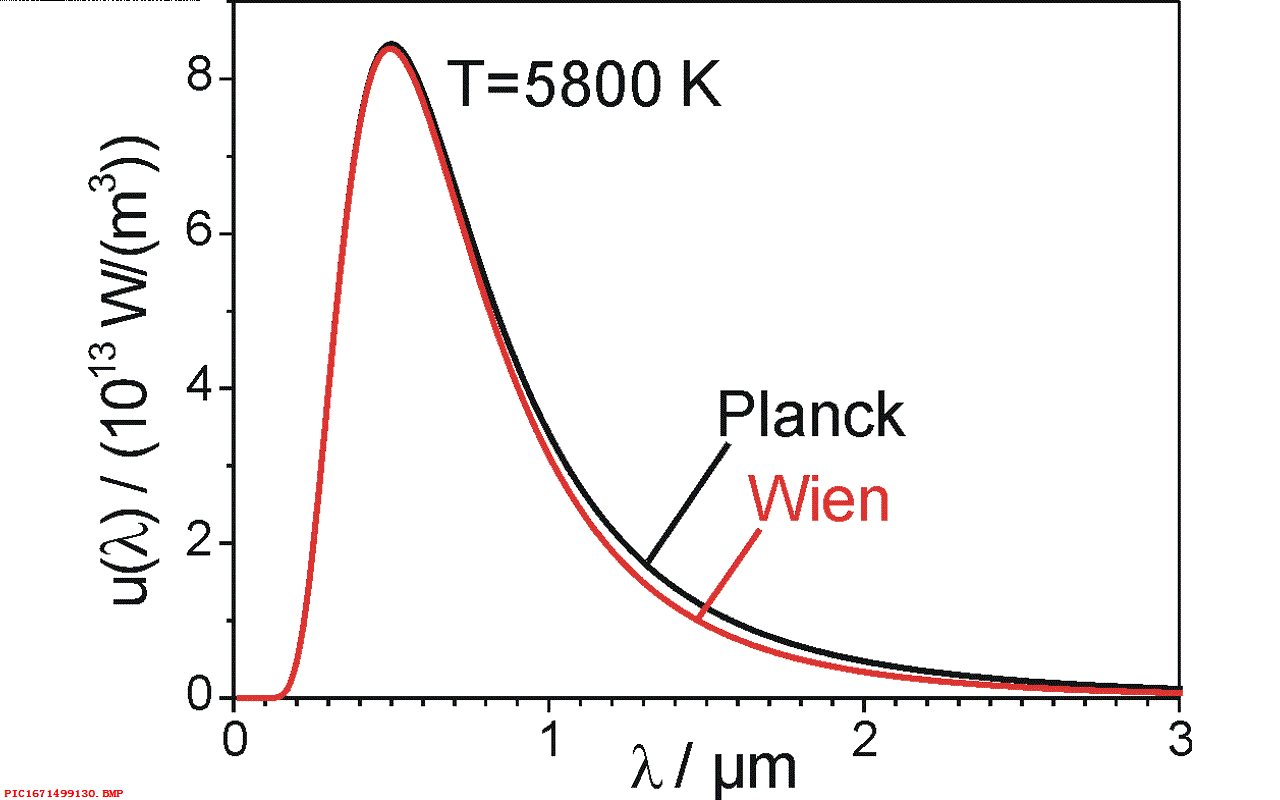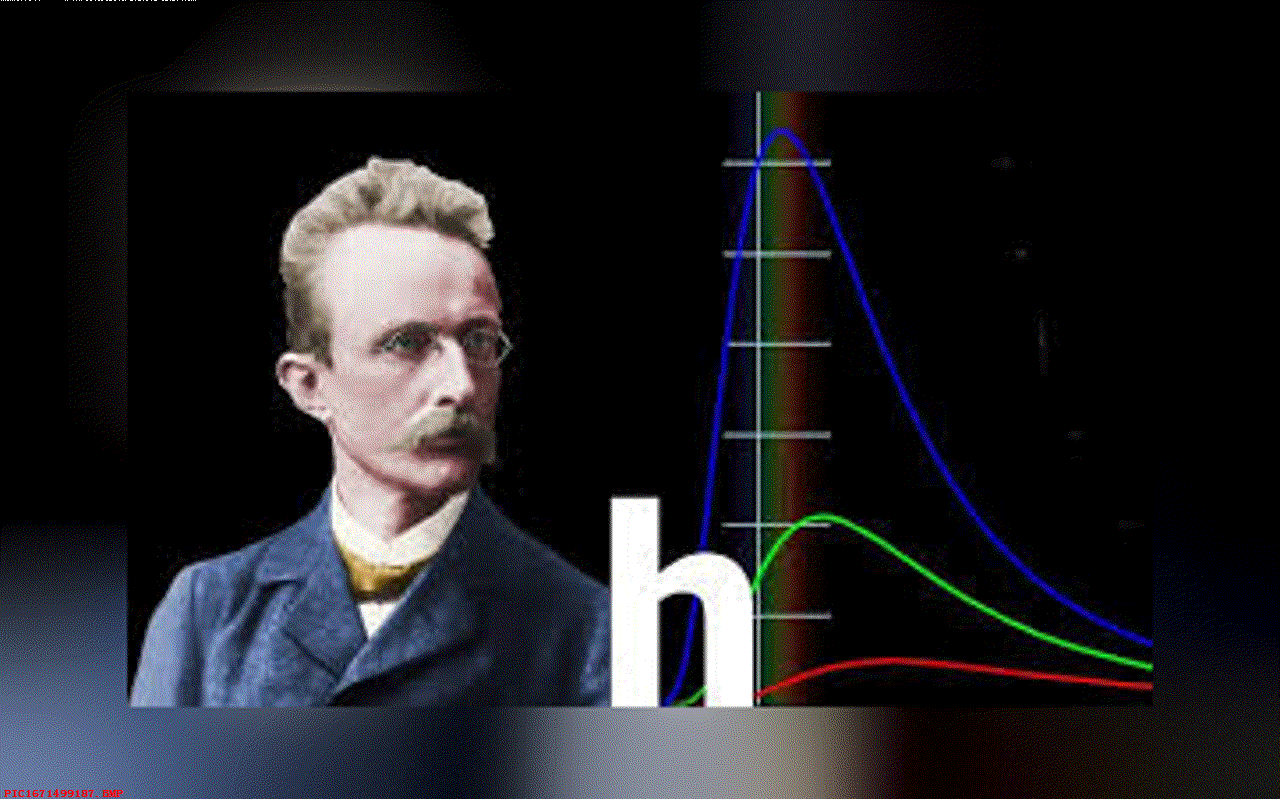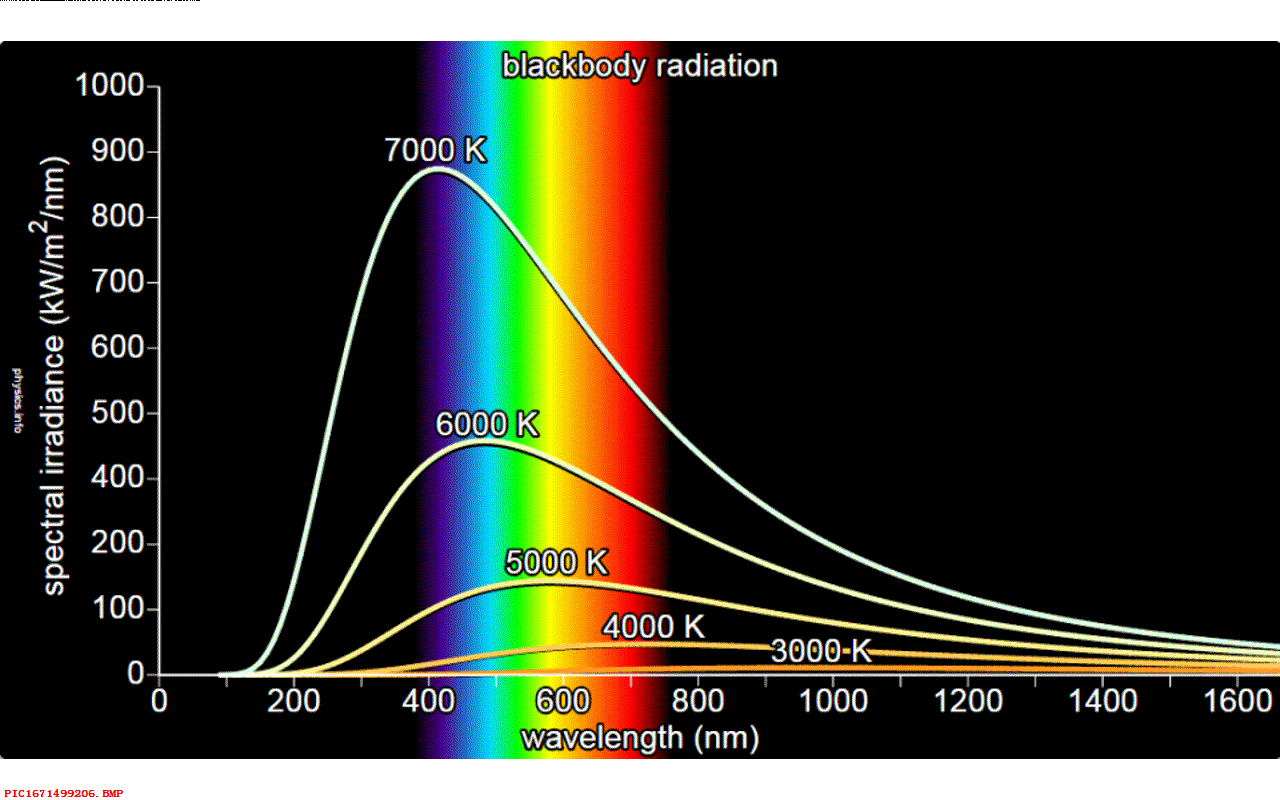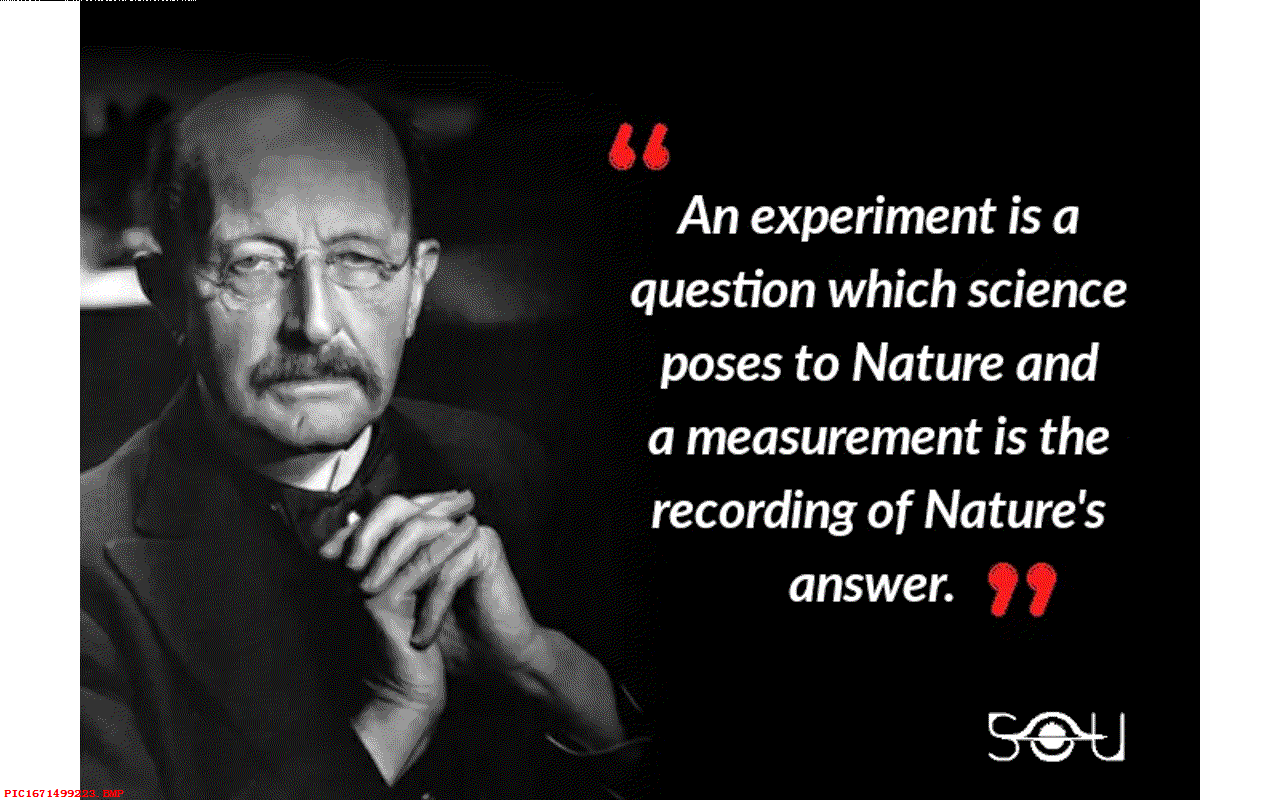
  同时，普朗克开始转向新的研究领域，这最终使他不得不接受玻尔兹曼关于概率的理论。 在1894年普朗克的一位好友，名叫威廉·维恩，他使用了一个方程来刻画黑体辐射能量分布曲线，这个方程是基于实验数据得到的，并没有多少理论能够支持这个公式。 普朗克认为他有解决这个理论问题的独特的方法，这是因为他对熵的概念有别人没有过的担忧。 几年后他回忆道，世事无常，原来对于熵毫无兴趣的同事们现在对待熵都跟打了鸡血似的兴奋起来。  到了1899年，普朗克发表了他的研究结果，不久这个公式被称为普朗克-维恩定理。

  但是这个公式在光谱低频率段效果并不好。 到了1900年十月份，一位实验研究人员告诉普朗克需要调整他的方程。 为此普朗克随手对公式进行了调整，低频和高频段与维恩公式都符合的很好。 实验人员很满意，但普朗克却开始抓狂了。 一位理论物理学家不仅仅是对实验数据给出一个描述的方程，他们需要从最基础理念来将公式推导出来。

  他后来回忆道，整整六年我一直都在对黑体辐射问题的答案苦苦寻觅。 对于该问题的重要性和求解答案我心知肚明，我需要在不违反热力学两个定理的前提下不惜代价去找到理论解释。 自己形容当时就像抓住一根救命稻草那样，他转向了玻尔兹曼关于熵的统计方法。

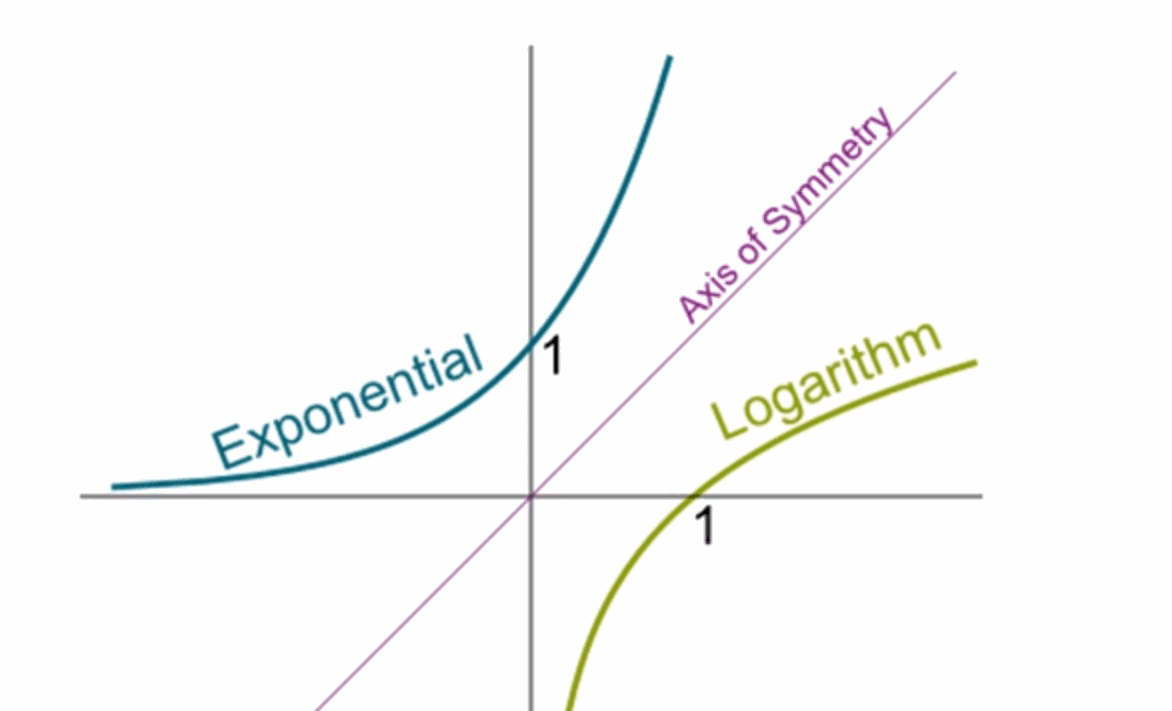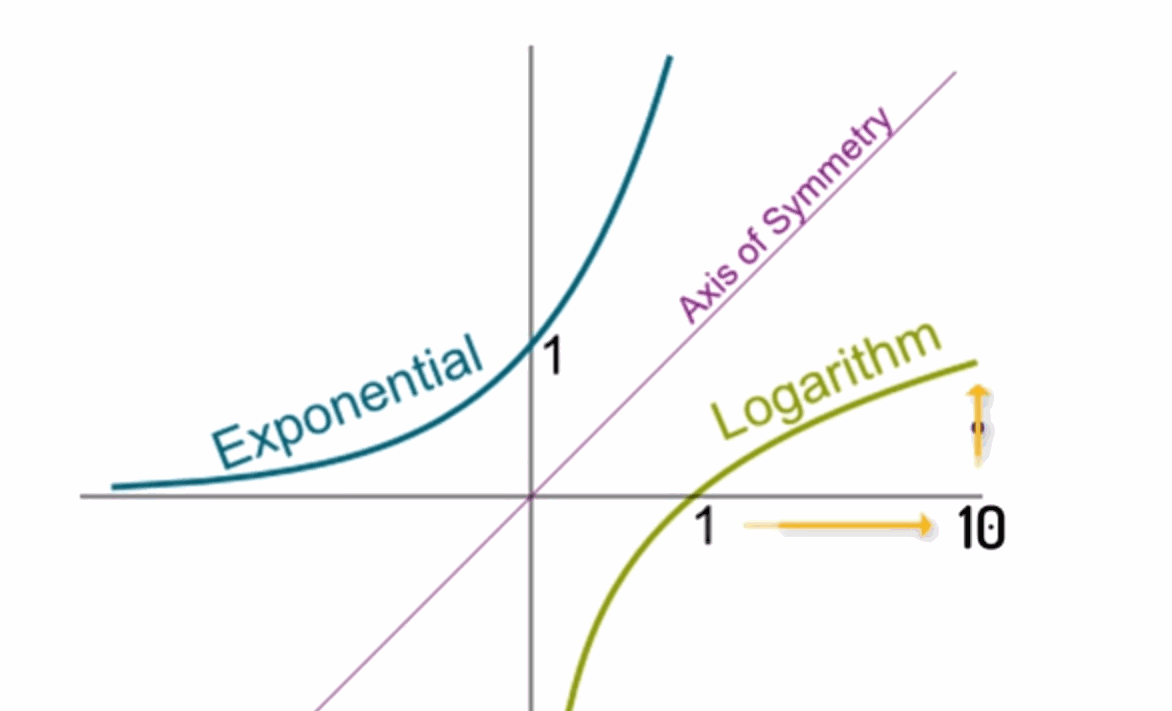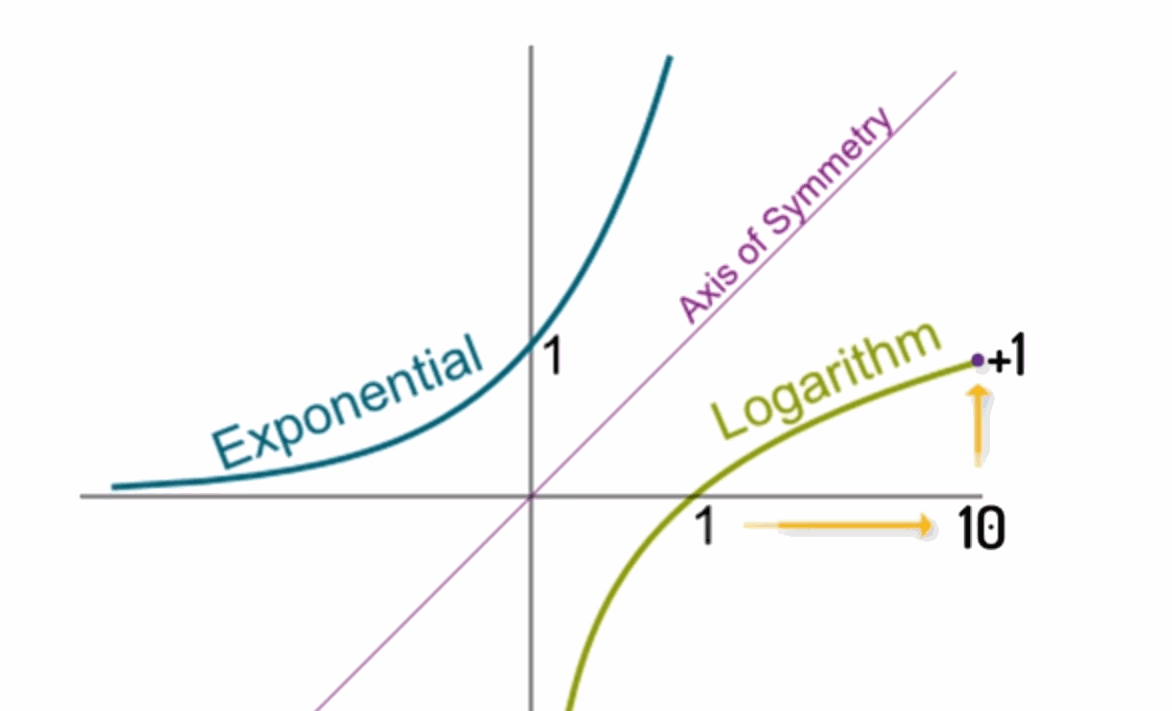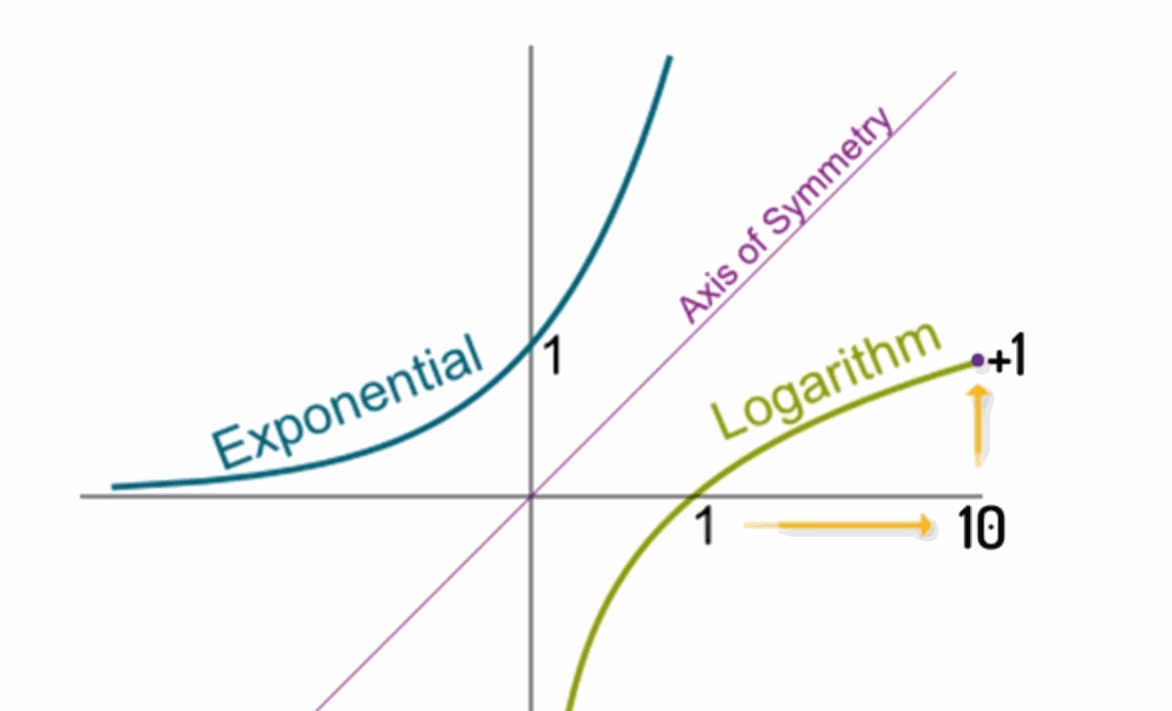
  经过几周没日没夜的工作， 普朗克得出了如下的结论， 既然熵 s 是一个相加的量，但概率 W 是相乘的量，因此我就得到一个简单的假设，那就是 s 等于k 乘以 log(W)，k 是通用常量。l og函数是指数函数的反函数，自变量乘以10，它对应的对数值增加1，对数可以把相乘运算转换成相加运算。

八、熵公式的应用

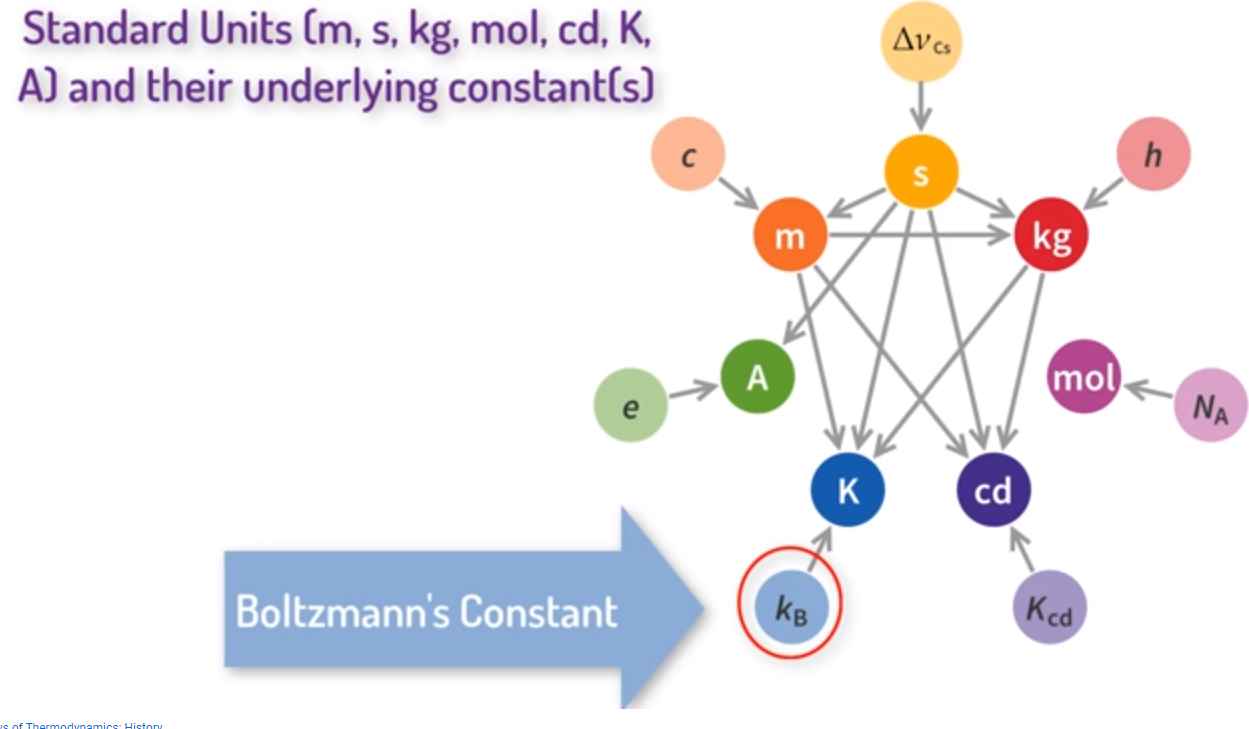
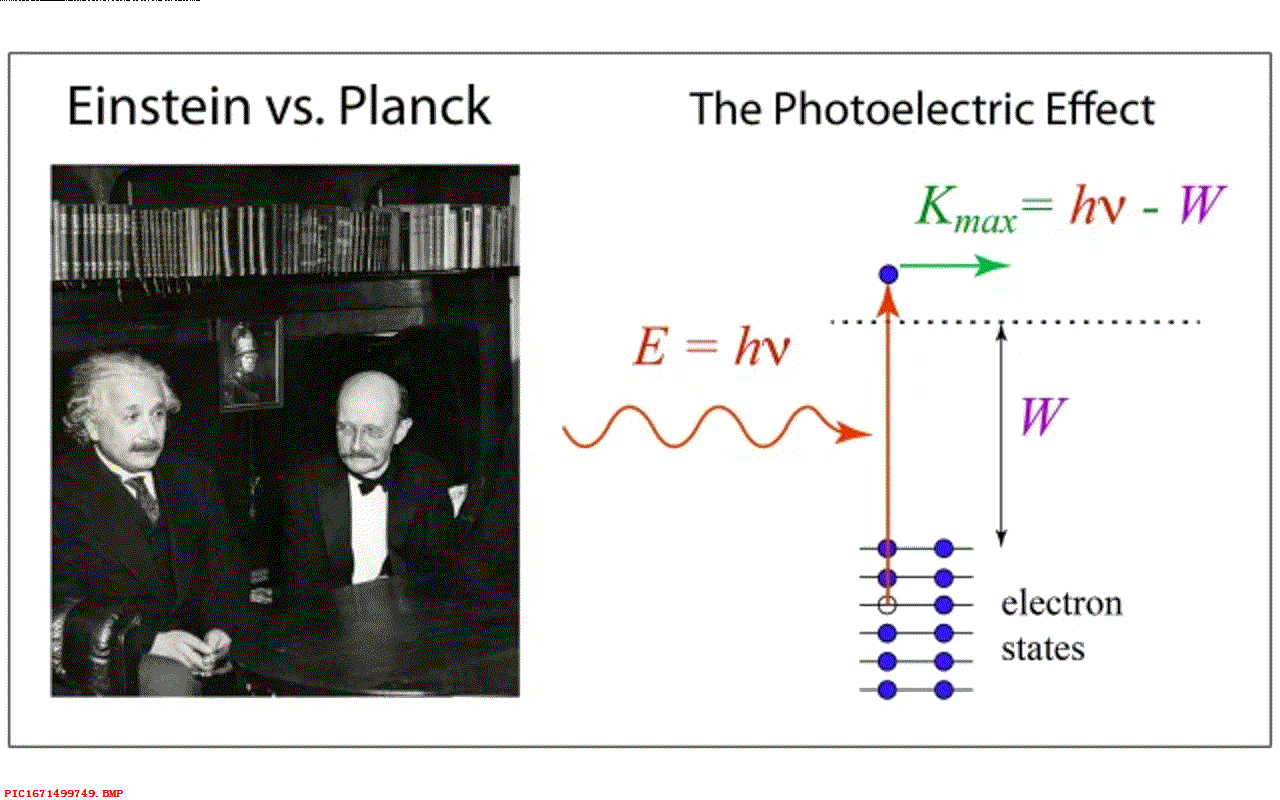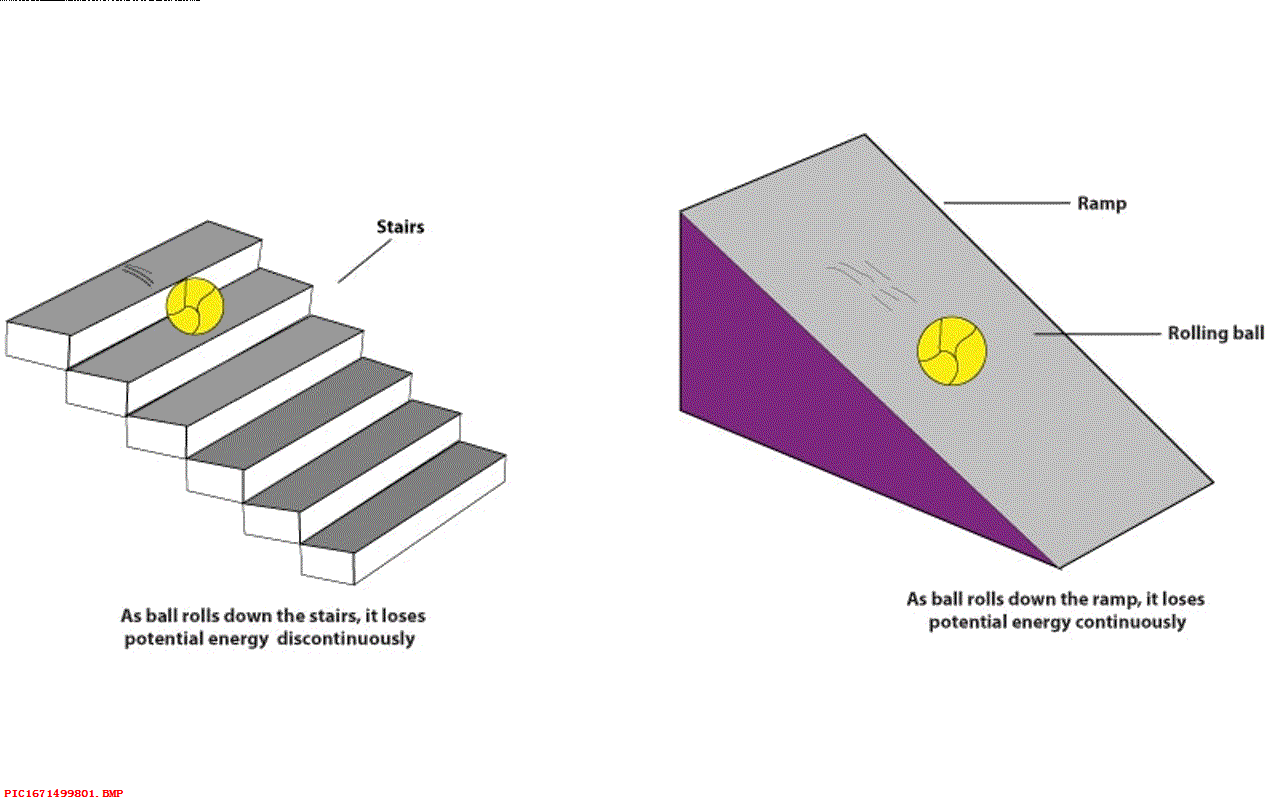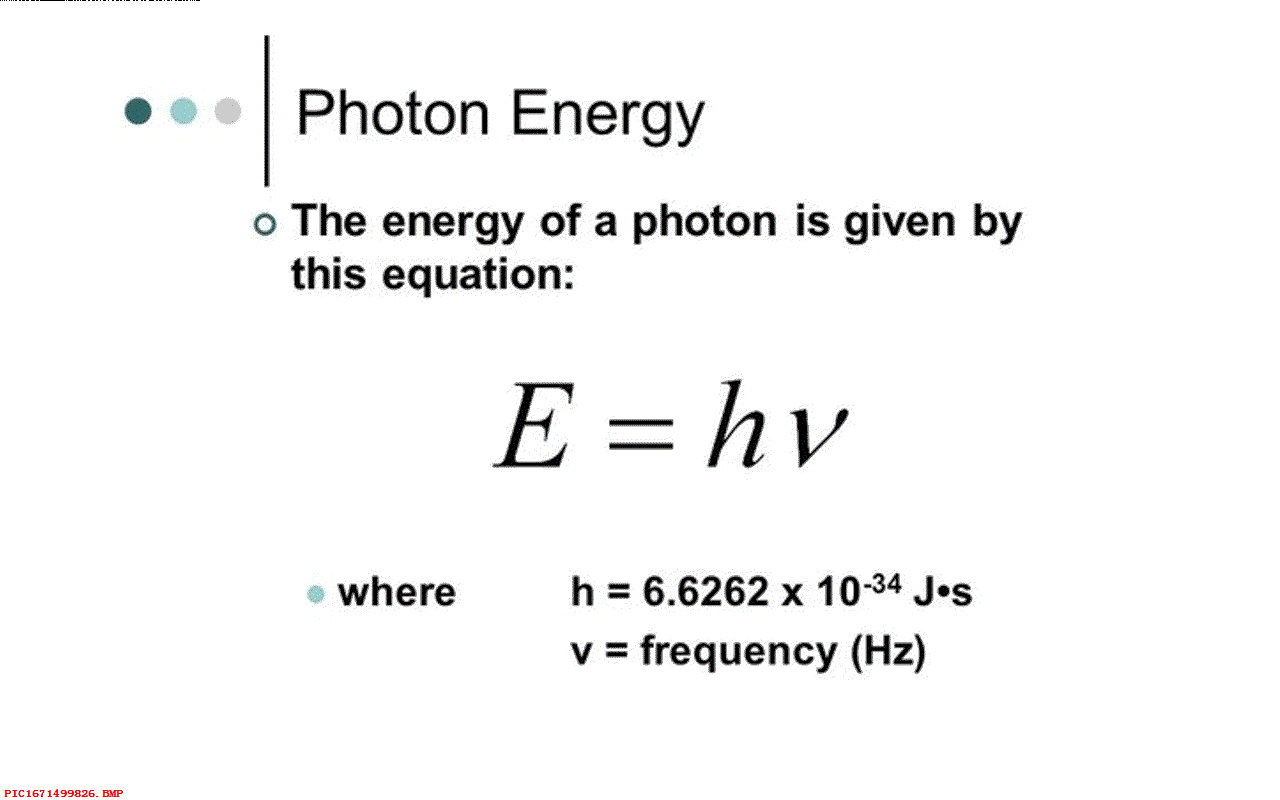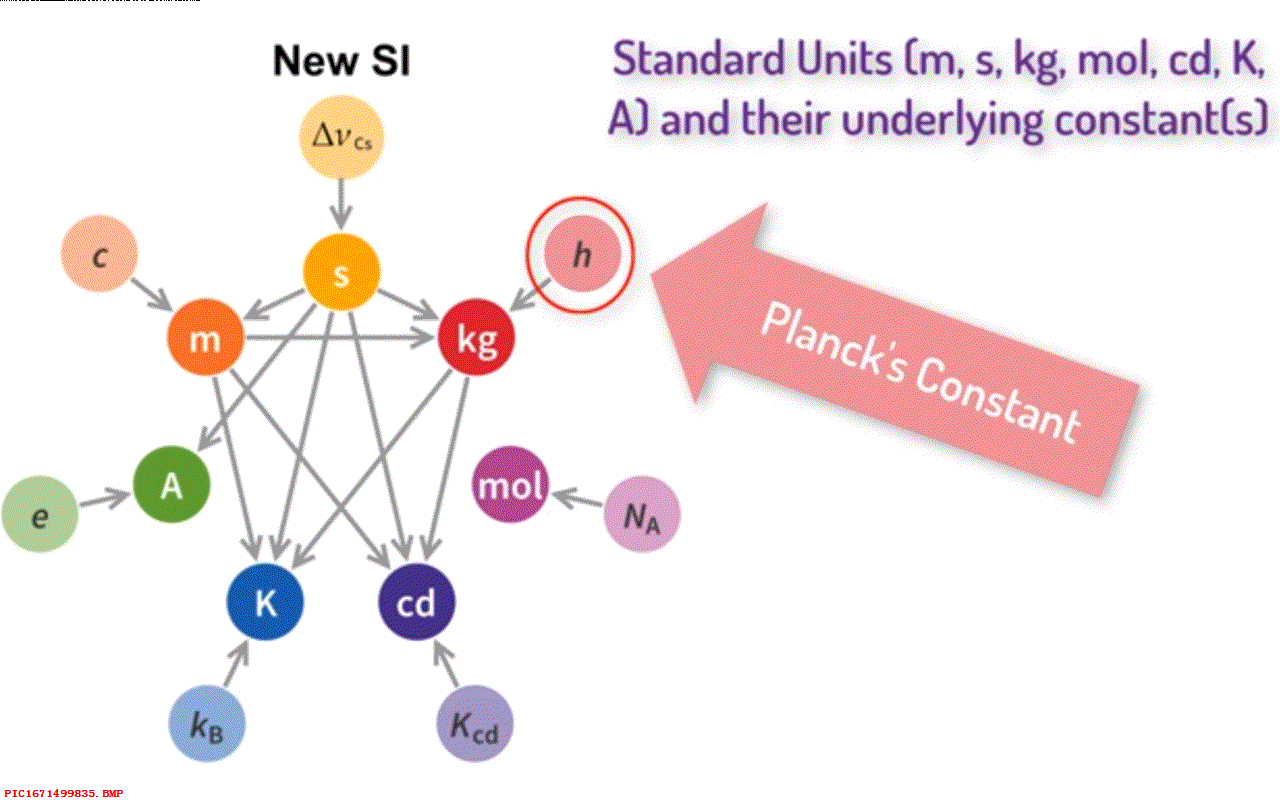
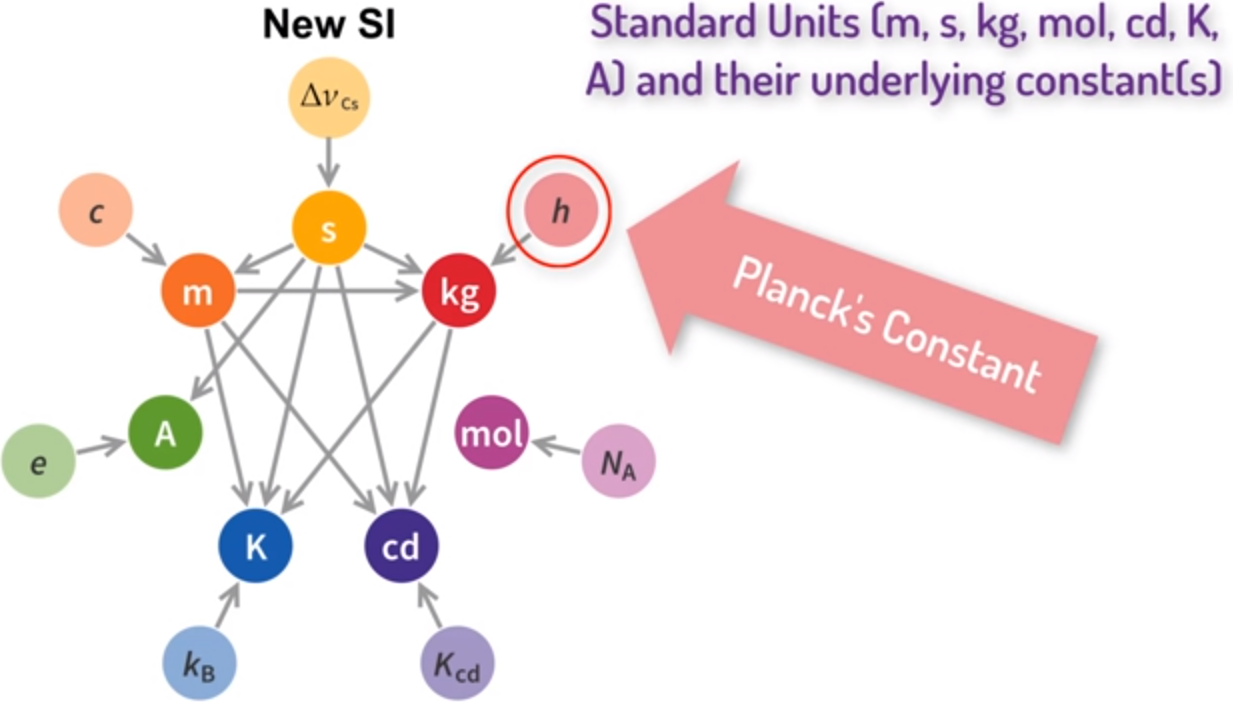
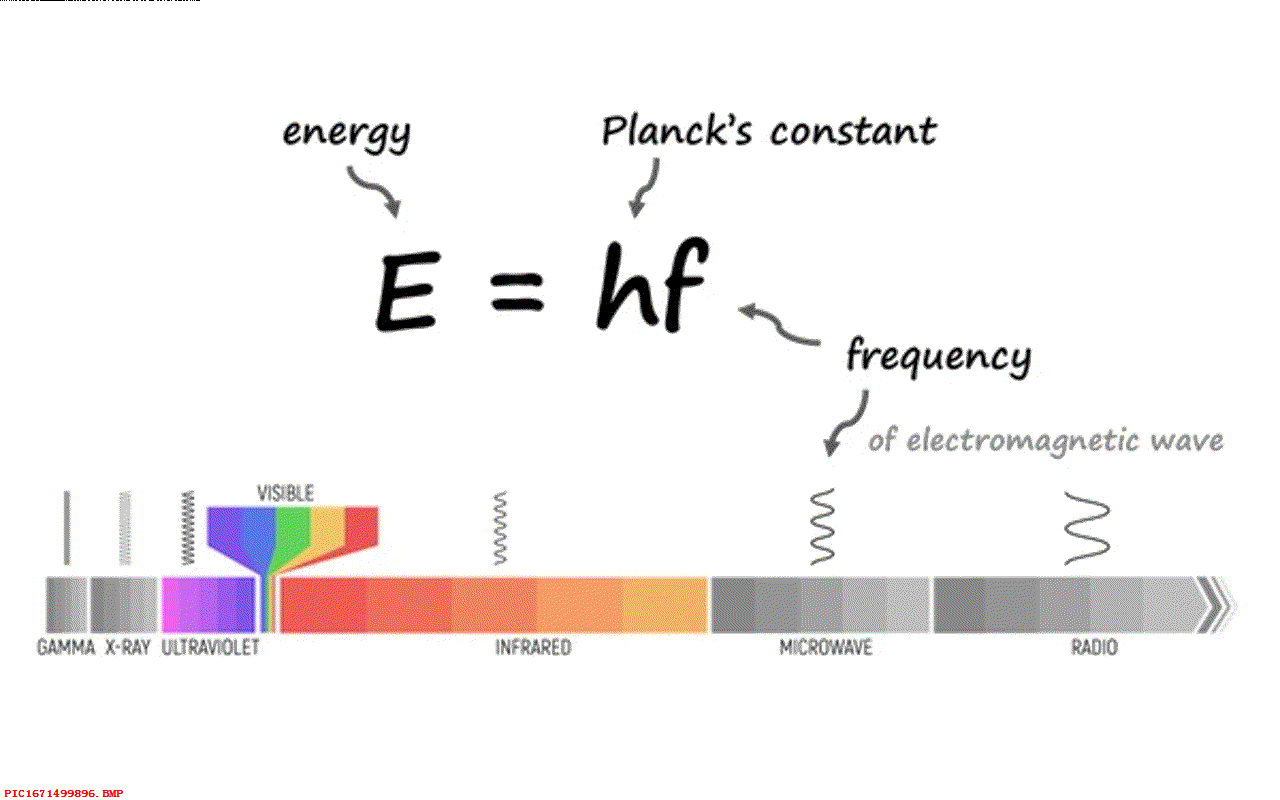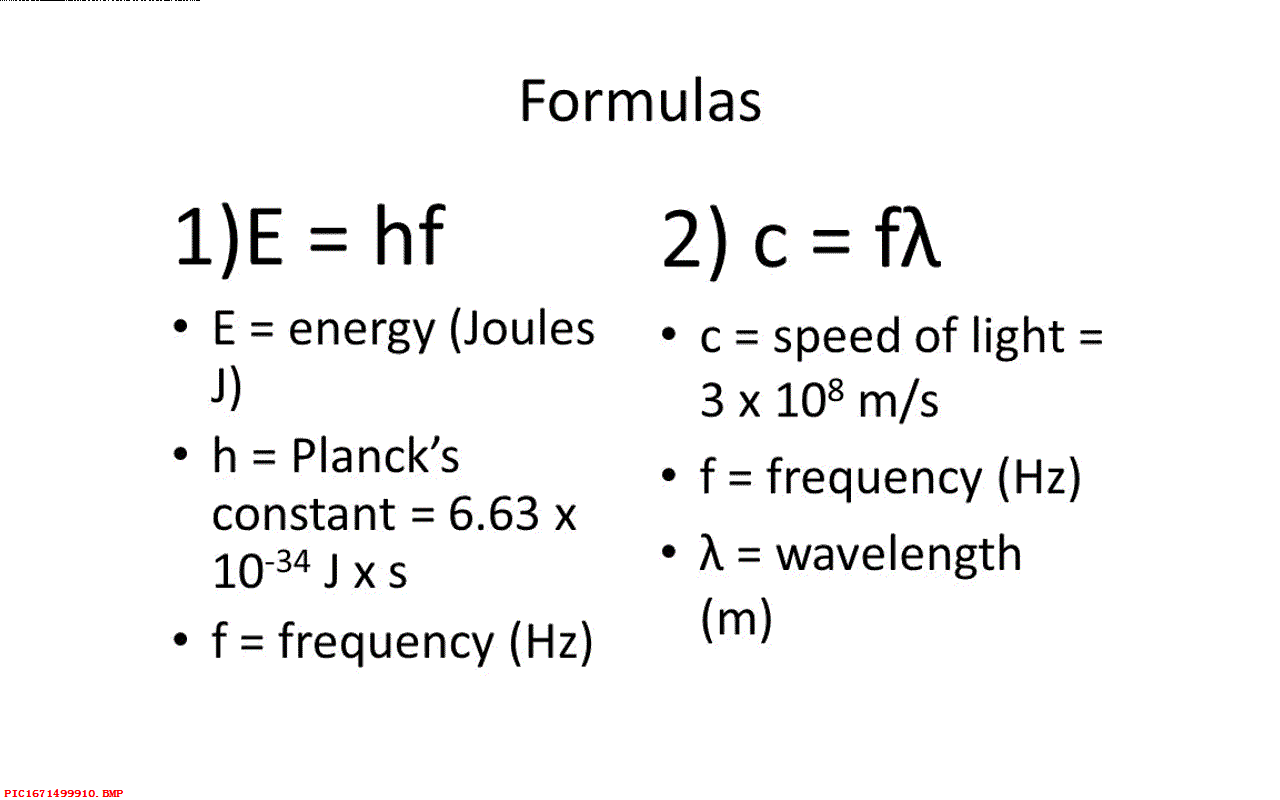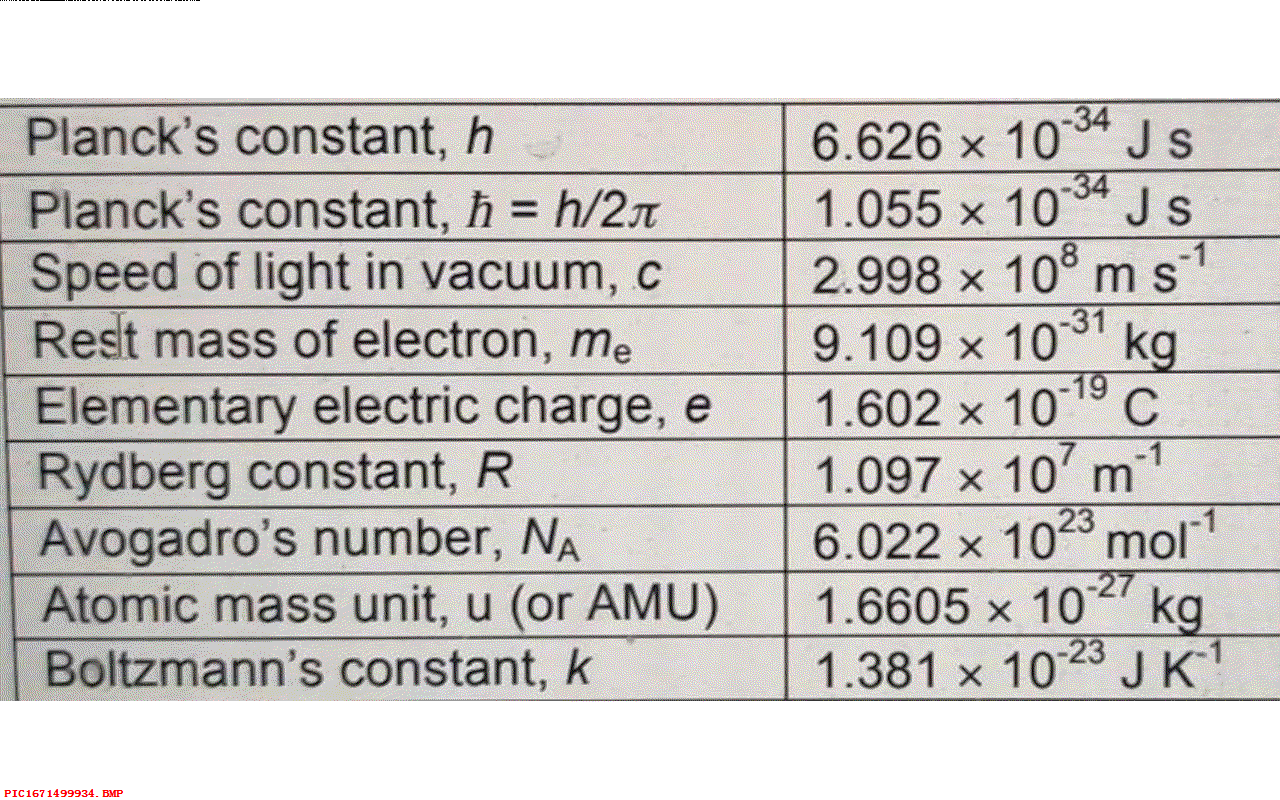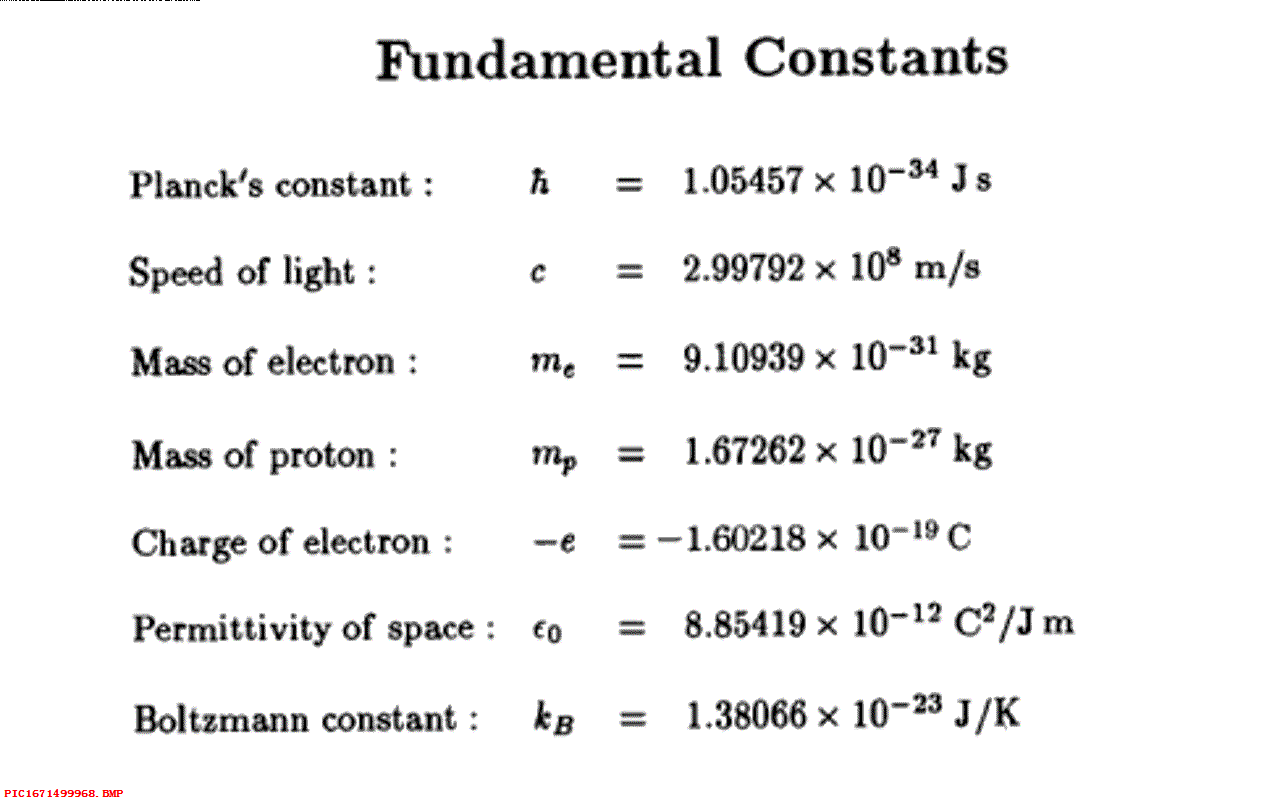
  这就是著名的熵的数学公式，但它的物理含义是什么呢？ 首先，它表明熵可以从分子的概率中计算出来。由于不像温度那样可以比较方便的被测量到，对于物体的任何一种分子的分布它的熵是确定的值，分布越复杂，对应的熵越大。 其次，常量 k 不仅仅表明了概率和熵之间的关系，k 在很多方程中都有应用，包括热容量公式、粒子动能与温度之间的关系。 利用 k 的精确值，人们可以预测很多在当时还无法精确获知的微观事情，比如氢原子的质量，甚至电子的电荷。 实际上，到了2019年 k 还是物理中七个基础常量之一，比如光的速度，现在我们使用的物理计量单位都依赖于它。

  但是普朗克遇到了问题，如果能量是连续的，那么它可以分割成无穷的不同能量组合形式，对应的概率也会发散，对应的熵也会是无穷大。 普朗克对此解释，如果能量被认为是连续可分，这种分布就可能是无穷多种形式。 为此，普朗克将热辐射能量限制为一些小的能量包，对应的能量等于常量 h 乘以对应的频率。 这是量子力学的最初起源，因此玻尔兹曼的熵理论推动了量子革命。 注意，这里的 h 也是七种物理常量之一，确定了我们的单位计量。

  随着黑体辐射实验数据增加，普朗克设法计算出两个常量 h，k 的数值。 令人惊讶的是，他所得到的 h 的值与现在测量值仅仅只有 1% 的差异，所测量 k 的值之比现在测量结果小了 1.5%。 利用所得到的 k 的数值，普朗克计算出电子的电荷，比起现在测量的数值误差只有 2%。 作为对比，当时另外两个被接收的电子电荷的数值则分别低了73%和高了35%。

九、玻尔兹曼公式与玻尔兹曼常数

  你也许会问，这个方程以及常量为何以玻尔兹曼命名，并被放在玻尔兹曼的墓碑上？ 但普朗克却在这个过程贡献最大。

  当普朗克第一次引入熵的方程的时候，他使用了一个新的方法。 他在论文中写道，这里引入了概率的概念，对于热力学第二定律的重要性是玻尔兹曼首先提出的。 他的这句话对于那些没有通读玻尔兹曼关于概率50页长文的人来说，意味着玻尔兹曼最初提出了这个方程。

  在1906年九月，玻尔兹曼因抑郁症而自杀了。 在这个期间，普朗克做了一系列关于热辐射的学术讲座。 通过玻尔兹曼科学回忆录我们知道，在普朗克给出他的熵公示的四年前，玻尔兹曼写出了与熵相关的函数同样与概率的对数相关。这一点有点令人迷惑。

  话说过来，正因为这个原因，普朗克在他的课程中称，关于熵与概率之间的对数关系是玻尔兹曼在1896年最初提出的。 并补充道，尽管玻尔兹曼从未提到常量，玻尔兹曼也从未直接将概率的对数与熵联系起来，他未明确给出关于熵的量。 但对此普朗克认为，关于熵的明确定义非常重要，因为它导致了量子假设的必要性。 几年后，普朗克把这些讲座集结成册出版， 不料产生了一个意想不到的结果，直到现在还被当做证据，来说明这个被普朗克提出的公式被玻尔兹曼命名的合理性。

  同样，在1910年左右，人们对于方程中的常量习惯使用方程的提出者的名字来命名。 比如，1913年尼尔斯·波尔写了关于原子结构的论文，他提出了普朗克 h， 光子能量 e 等于 h乘以f。 波尔的论文非常流行，爱因斯坦几年后对波尔的论文评价道，直到如今对我来说波尔的论文都是那么的神奇，这是人类思维殿堂中最和谐的旋律。

  波尔的论文发表半年后，两位英国科学家，艾策和欧内斯特·格里菲斯在一篇关于金属低温下原子温度文章中，这也是我所见到的第一次将 k 称为 玻尔兹曼常量。 当然这篇论文比不上波尔论文，但也包含了许多有趣的数据，同样也给出了关于固体量子力学的综述， 因此被广泛阅读，很快大多数科学家开始讨论量子力学，并熟悉普朗克常数和玻尔兹曼常数。

  到1920年，马克思·普朗克获得了诺贝尔奖。 他抱怨道，k 通常被称为玻尔兹曼常量，但对我来说这有点奇怪，据我说知玻尔兹曼本人从来没有讲过有这么个常量。 到了1930年左右，人们习惯于用理论提出者来命名方程，S = k log(w) 被称为熵的玻尔兹曼方程，是因为 k 在早先时候被人们称为 玻尔兹曼常量。

十、玻尔兹曼墓碑

  差不多同时期，维也纳的一位市议员看到玻尔兹曼的陵墓破旧衰败， 他说，维也纳和它的市民对这位天才人物非常骄傲，他们希望寻找一个配得上他更好的墓地。 为此他们将玻尔兹曼的遗体迁移到与布拉姆斯和贝多芬毗邻的墓地，并雕刻了一个大理石半身像， 当地的一位名叫汉斯·帝林的科学家在墓地石碑上加上了这个被称为玻尔兹曼最伟大的科学成就的公式， 即 s = k log(W)。

  这就是玻尔兹曼公式的由来，以及为何被刻在他的墓碑上。 也许事实上这个公式应该被称为普朗克熵公式，这个常量的名字叫做普朗克常量更确切一些。  不过我们已经有了普朗克常量 h 了，所以这里出现了更多的麻烦，这又有谁能够理得清楚呢？

■ 相关文献链接:

• Boltzmanns Entropy Equation: A History from Clausius to Planck

● 相关图表链接:

• 图1.1.1 玻尔兹曼的熵公式
• 图1.1.2 1901年普朗克论文中的熵公式
• 图1.1.3 玻尔兹曼墓碑上的公式
• 图1.2.1 克劳修斯提出熵的概念
• 图1.2.2 随机运动的气体分子
• 图1.2.3 格思里与克劳修斯
• 图1.3.3 法拉第与麦克斯韦
• 图1.3.4 玻尔兹曼
• 图1.3.5 路德维格·玻尔兹曼与丽莎·迈特纳
• 图1.4.3 一杯水与大海
• 图1.4.4 玻尔兹曼与麦克斯韦
• 图1.5.1 麦克斯韦与他的夫人
• 图1.5.2 玻尔兹曼与他的妻子
• 图1.5.3 麦克斯韦与他的墓碑
• 图1.6.1 普朗克
• 图1.6.2 普朗克与玻尔兹曼
• 图1.7.1 普朗克-维恩定律
• 图1.7.2 指数函数与对数函数
• 图1.8.1 玻尔兹曼常数
• 图1.8.2 普朗克常数
• 图1.9.1 普朗克关于熵的起源叙述
• 图1.9.2 波尔与爱因斯坦
• 图1.10.1 汉斯·帝林与墓碑上的公式

今天的文章玻尔兹曼熵公式 s=klnω_玻尔兹曼常数k与R的关系分享到此就结束了，感谢您的阅读。