计算机进位制的计算方法_计算机进位制的计算方法

进位计数制

十进制计数法

• 古印度人大门的阿拉伯数字：0，1，2，3，4，5，6，7，8，9；

• 符号反映权重，符号的所在位置也反映权重（位权）

例：975.36
= 9 * 100 + 7 * 10 + 5 * 1 + 3 * 0.1 + 6 * 0.01
= 9 * 10^2 + 7 * 10^1 + 5 * 10^0 + 3 * 10^-1 + 6 * 10^-2
=>
十进制：
K(n) K(n-1) ... K(2) K(1) K(0) K(-1) K(-2) ... K(-m)
= K(n) * 10^n + K(n-1) * 10^(n-1) + ... + K(2) * 10^2 + K(1) * 10^1 + K(0) * 10^0 + K(-1) * 10^-1 + K(-2) * 10^-2 + ... + K(-m) * 10^-m

r进制计数法

• 基数：每个数码位所用到的不同符号的个数，r进制的基数为r

K(n) K(n-1) ... K(2) K(1) K(0) K(-1) K(-2) ... K(-m)
= K(n) * r^n + K(n-1) * r^(n-1) + ... + K(2) * r^2 + K(1) * r^1 + K(0) * r^0 + K(-1) * r^-1 + K(-2) * r^-2 + ... + K(-m) * r^-m

• 二进制：0，1

• 例：101 => 1 * 10^2 + 0 * 10^1 + 1 * 10^0 = 5.5

• 八进制：0，1，2，3，4，5，6，7

• 例：5.4 => 5 * 8^0 + 4 * 8^-1 = 5.5

• 十进制：0，1，2，3，4，5，6，7，8，9

• 例：5.5 => 5 * 10^0 + 5 * 10^-1 = 5.5

• 十六进制：0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F

• 例：5.8 => 5 * 16^0 + 8 * 16^-1 = 5.5

任意进制 → 十进制

• 二进制→十进制

• r进制计数法

10010010.110 => 1 * 10^7 + 1 * 10^4 + 1 * 10 ^1 + 1 * 10^-1 + 1 * 10^-2 = 146.75

• 利用位权计算

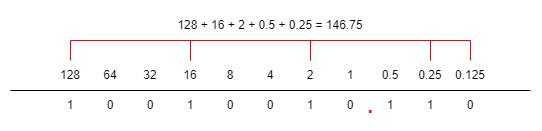
• 八进制→十进制

251.5 => 2 * 8^2 + 5 * 8^1 + 1 * 8^0 + 5 * 8^-1 = 168.625

• 十六进制→十进制

AE86.1 => 10 * 16^3 + 14 * 16^2 + 8 * 16^1 + 6 * 16^0 + 1 * 16^-1 = 44678.0625

二进制 ←→ 八进制、十六进制

• 二进制→八进制：∵2^3 = 8；∴3位一组，每组转换和曾对应的八进制符号

1111000010.01101 => 001 111 000 010.011 010 => [1] [4 + 2 + 1] [0] [2] . [2 + 1] [2] => 1702.32

• 二进制→十六进制：∵2^4 = 16；∴4位一组，每组转换和曾对应的十六进制符号

1111000010.01101 => 0011 1100 0010.0110 1000 => [2 + 1] [8 + 4] [2] . [4 + 2] [8] => 3C2.68

• 八进制→二进制：每位八进制对应的3位二进制

(251.5)8 => [2] + [4 + 1] [1] . [4 + 1] => 010 101 001 . 101 = (010101001.101)2

• 十六进制→二进制：每位十六进制对应的4位二进制

(AE86.1)16 => [10] [14] [8] [6] . [1] => [8 + 2] [8 + 4 + 2] [8] [4 + 2] . [1] => 1010 1110 1000 0110 . 0001 => (1010111010000110.0001)2

各种进制常见书写方式

二进制（binary）：(1010001010010)2、1010001010010B

八进制：(1652)8

十进制（decimalism）：(1652)10、1652D

十六进制（hexadecimal）：(1652)16、1652H、0x1652

十进制 → 任意进制

• 整数部分：除基取余法

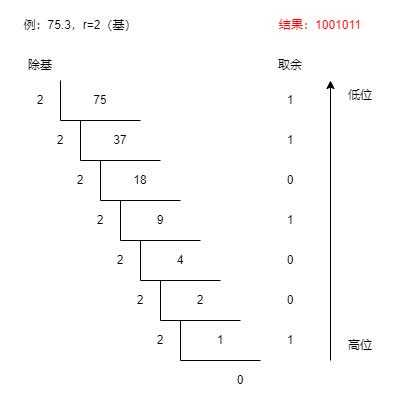
• 小数部分：乘基取整法

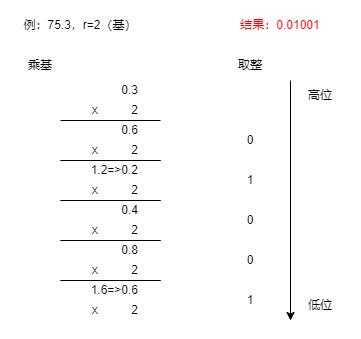
• 拼凑法

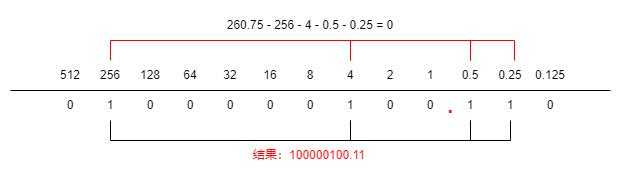
真值：符合人类习惯的数字 +15、-8

机器数：数字实际存到机器里的形式，正负号需要被数字化 +15 → 0 1111；-8 → 1 1000