16 多校 10 – B – Hard problem （HDU – 5858 ）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5858

推公式

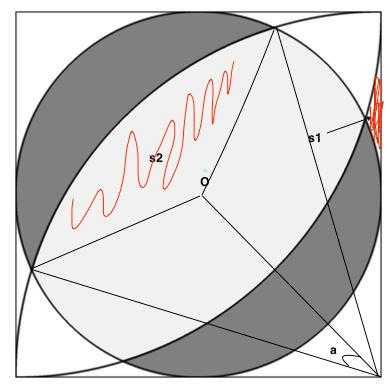
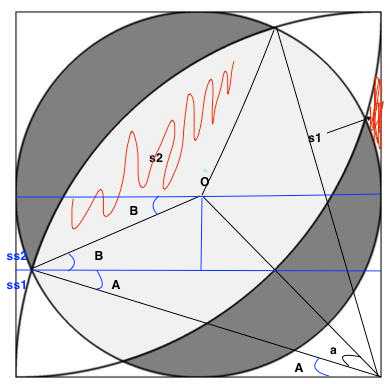
角a是突破点。用余弦公式就可以求出a的余弦值了。
1、求s2（较容易）
就是扇形减去两个三角形的面积。用S = 0.5*a*b*sinc就可以求出三角形的面积。扇形面积是 S = 0.5 * a * r * r 。求出s2后就可以用小圆内扇形面积减去s2 ，就得到一半的阴影面积了。

#include<iostream>
#include<stdio.h>
#include<math.h>
using namespace std;
double pi = acos(-1),l,r,a = acos(5*sqrt(2)/8),b = acos(-sqrt(2)/4),c = 2 * (pi - b);//b为三角形钝角弧度，c为小圆内扇形圆心角弧度。
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        scanf("%lf",&l);//正方形边长、大圆半径
        r = l / 2;//小圆半径
        double s1 = 2 * sqrt(2) * r * r * sin(a);//两三角形面积之和
        double s2 = a * l * l;//大扇形面积
        double s3 = s2 - s1;//图中s2部分面积
        double s4 = 0.5 * c * r * r;//小扇形面积
        double s = s4 - s3;//一半阴影面积
        s = s * 2;
        printf("%.2lf\n",s);
    }
    return 0;
}

2、求s1

s1 = ss1 + ss2.
ss1 和 ss2 的面积均为一个长方形减去一个三角形和一个扇形。

阴影面积的一半就为：
正方形面积 – 四分之一大圆面积 – 2 * s1 – （正方形面积 – 小圆面积）／4

#include<iostream>
#include<string.h>
#include<stdio.h>
#include<math.h>
using namespace std;
double pi=acos(-1),A=pi/4-acos(5*sqrt(2)/8),B = asin(1-2*sin(A)),l,r;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        scanf("%lf",&l);
        double s1 = l*l*sin(A) - l*sin(A)*l*cos(A)*0.5 -A*0.5*l*l;
        r = 0.5*l;
        double s2 = r*(r-l*sin(A)) - ((r- l*sin(A))*(l*cos(A)-r)*0.5) - 0.5*B*r*r ;
        double ss = s1+s2;
        double s = (l*l-pi*l*l/4) -ss*2- 0.25*(l*l-pi*r*r);
        printf("%.2f\n",s*2);
    }
    return 0;
}

今天的文章16 多校 10 – B – Hard problem （HDU – 5858 ）分享到此就结束了，感谢您的阅读。