算法设计与分析第四章课后答案_关于计算机体系结构的思维导图

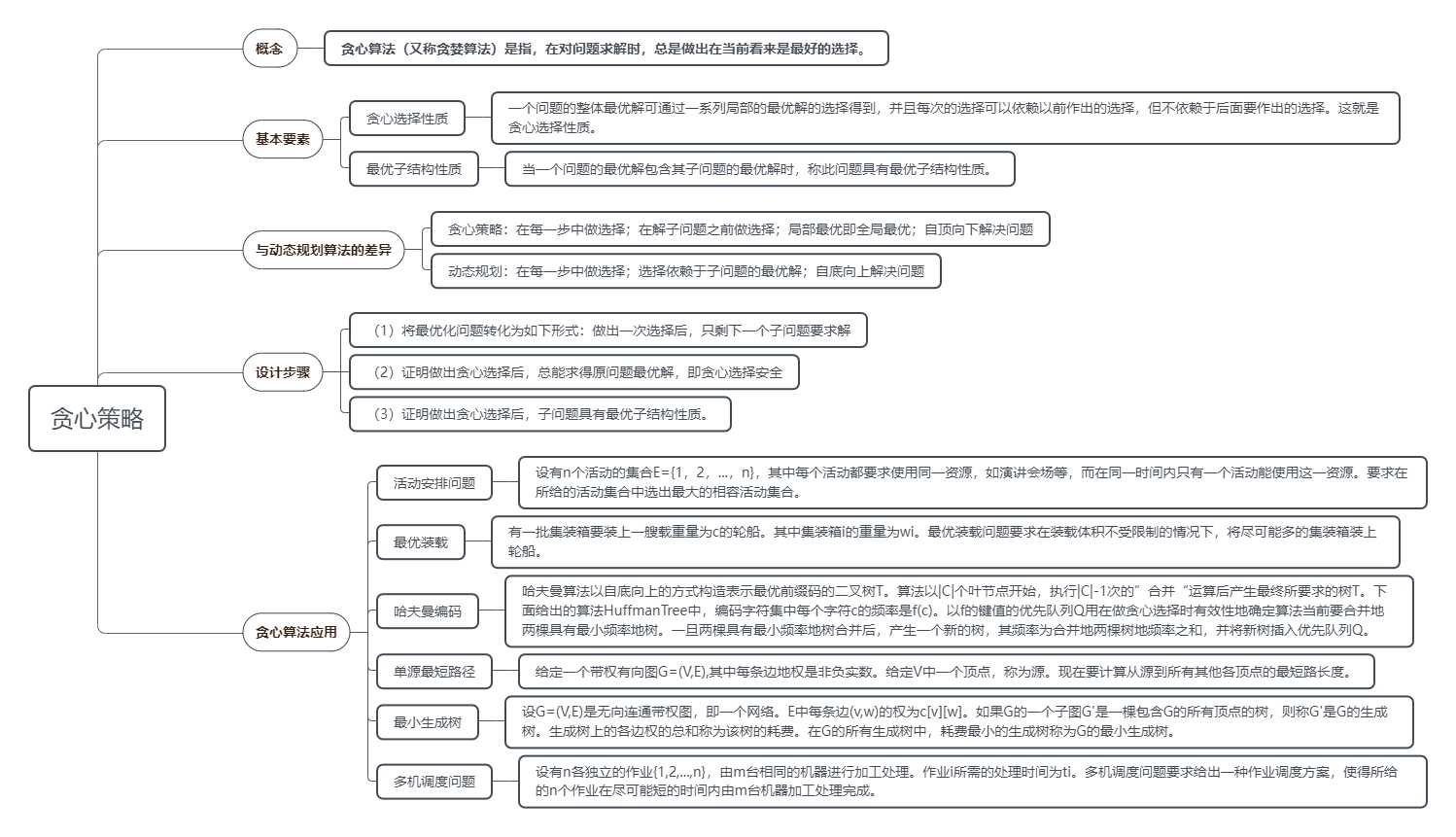
详细内容、问题介绍、算法思想、贪心选择性质、最优子结构性质、部分代码均在下文展示。 

贪心算法的概念
贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。

贪心算法的基本要素
（1）贪心选择性质
        一个问题的整体最优解可通过一系列局部的最优解的选择得到，并且每次的选择可以依赖以前作出的选择，但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。
        对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每步所做的贪心选择最终导致问题的整体最优解。首先考察问题的一个整体最优解，并证明可修改这个最优解，使其以贪心选择开始。做了贪心选择后，原问题简化为规模更小的类似子问题。然后用数学归纳法证明，通过每一步做贪心选择，最终可得到问题的整体最优解。其中，证明贪心选择后的问题简化为规模更小的类似子问题的关键在于，利用该问题的最优子结构性质。

（2）最优子结构性质
        当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。

贪心算法与动态规划算法的差异

贪心策略：在每一步中做选择；在解子问题之前做选择；局部最优即全局最优；自顶向下解决问题

动态规划：在每一步中做选择；选择依赖于子问题的最优解；自底向上解决问题

动态规划算法中，每步所做的选择往往依赖于相关子问题的解。因而只有在解出相关自子问题后，才能做出选择。而在贪心算法中，仅在当前状态下做出最好选择，即局部最优选择。再去解做出这个选择后产生的相应子问题。贪心算法所作的贪心选择可以依赖以往所做过的选择，但决不依赖将来所做的选择，也不依赖子问题的解。
正是由于这种差别，动态规划算法通常以自底向上的方式解决各子问题，贪心算法则通常以自顶向下的方式进行，以迭代的方式做出相继的贪心选择，每做一次贪心选择，就将所求问题简化为规模更小的子问题。

贪心算法设计步骤

（1）将最优化问题转化为如下形式：做出一次选择后，只剩下一个子问题要求解
（2）证明做出贪心选择后，总能求得原问题最优解，即贪心选择安全
（3）证明做出贪心选择后，子问题具有最优子结构性质。

贪心算法应用

活动安排问题

题目描述：设有n个活动的集合E={1，2，…，n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。要求在所给的活动集合中选出最大的相容活动集合。

算法思想：将活动按照结束世界升序排列，一开始选择活动1，并将j初始化为1，然后依次检查活动i是否与当前已选择的所有活动相容。若 相容，则将活动i加入到已选择活动的集合A中；否则不选择活动i，而继续检查下一活动与集合A中活动的相容性。

template<class type>
void GreedySelector(int n,Type s[],Type f[],bool A[])
{
    A[1]=true;
    int j=1;
    for(int i=2;i<=n;i++){
        if(s[i]>=f[j]){
            A[i]=true;
            j=i;
        }
        else{
            A[i]=false;
        }
    }
}

最优装载

题目描述：有一批集装箱要装上一艘载重量为c的轮船。其中集装箱i的重量为wi。最优装载问题要求在装载体积不受限制的情况下，将尽可能多的集装箱装上轮船。

算法思想：采用重量最轻者先装的贪心选择策略，可产生最优装载问题的最优解。

贪心选择性质：设集装箱已依其重量从小到大排序，(x1,x2,…,xn)是最优装载问题的一个最优解，设k=min{i|xi=1}1<=i<=n,如果给定的最优的装载问题有解，则1<=k<=n。

        1.当k=1时，(x1,x2,…,xn)是一个满足贪心选择性质的最优解。

        2.当k>1时，取y1=1，yk=0，yi=xi，1<i<=n，i!=k,则                        

        因此，(y1,y2,…,yn)是所给最优装载问题的可行解。

最优子结构性质：设(x1,x2,…,xn)是最优装载问题的满足贪心选择性质的最优解，则x1=1，(x2,x3,…,xn)是轮船载重量为c-w1、待装船集装箱为{2,3,…,n}时相应最优装载问题的最优解

template<class Type>
void Loading(int x[],Type w[],Type c,int n){
    int *t = new int [n+1];
    Sort(w,t,n);
    for(int i=1;i<=n;i++)
        x[i]=0;    
    for(int i=1;i<=n&&w[t[i]]<=c;i++){
        x[t[i]]=1;
        c-=w[t[i]];
    }
}

哈夫曼编码

题目描述：哈夫曼算法以自底向上的方式构造表示最优前缀码的二叉树T。算法以|C|个叶节点开始，执行|C|-1次的”合并“运算后产生最终所要求的树T。下面给出的算法HuffmanTree中，编码字符集中每个字符c的频率是f(c)。以f的键值的优先队列Q用在做贪心选择时有效性地确定算法当前要合并地两棵具有最小频率地树。一旦两棵具有最小频率地树合并后，产生一个新的树，其频率为合并地两棵树地频率之和，并将新树插入优先队列Q。

贪心选择性质：

设C是编码字符集，C中字符c的频率为f(c)，又设x和y是C中具有最小频率的两个字符，则存在C的最优前缀码使得x和y具有相同的码长且仅最后一位编码不同

最优子结构性质：

设T是表示字符集C的一个最优前缀码的完全二叉树。C中字符c的出现频率位f（c）。设x和y是树T的两个叶子且为兄弟，z是它们的父亲。若将z看作具有频率f(z)=f(x)+f(y)的字符，则树T’=T-{x,y}表示字符集C’=C-{x,y}∪{z}的一个最优前缀码。

void HuffmanTree(int n)//使用优先队列
{
	for(int i=1;i<n;i++){
		HTree x=Top();
		Pop();
		HTree y=Top();
		Pop();
		HTree N=MakeTree(0,x->parent,y->parent,x->weight+y->weight,0);
		Insert(N);
	}
}

单源最短路径

题目描述：给定一个带权有向图G=(V,E),其中每条边地权是非负实数。给定V中一个顶点，称为源。现在要计算从源到所有其他各顶点的最短路长度。

算法思想：设置顶点集合 S ，不断地做贪心选择来扩充这个集合。一个顶点属于集合 S 当且仅当从源到该顶点的最短路径长度已知。初始时，S 中仅有源。设 u 是 G 的某一个顶点，把从源到 u 且中间只经过 S 中顶点的路称为从源到 u 的特殊路径，并用数组 dist 记录当前每个顶点所对应的最短特殊路径长度。Dijkstra 算法每次从 V – S 中取出具有最短特殊路径长度的顶点 u ，将 u 添加到 S 中，同时对数组 dist 做必要的修改。一旦 S 包含了所有 V 中顶点，dist 就记录了从源到所有其他顶点之间的最短路径长度。

void dijkstra(int n,int v)
{
	for(int i=1;i<=n;i++){
		dist[i]=map[v][i];
		s[i]=false;
		if(dist[i]==Inf)
			pre[i]=0;
		else pre[i]=v;
	}
	dist[v]=0;
	s[v]=true;
	for(int i=1;i<n;i++){
		int temp=Inf;
		int u=v;
		for(int j=1;j<=n;j++)
			if((!s[j])&&(dist[j]<temp)){
				u=j;
				temp=dist[j];
			}
			s[u]=true;
			for(int j=1;j<=n;j++){
				if((!s[j])&&(map[u][j]<Inf)){
					int newdist=dist[u]+map[u][j];
					if(newdist<dist[j]){
						dist[j]=newdist;
						pre[j]=u;
					}
				}
			}
	}
}

最小生成树

题目描述：设G=(V,E)是无向连通带权图，即一个网络。E中每条边(v,w)的权为c[v][w]。如果G的一个子图G’是一棵包含G的所有顶点的树，则称G’是G的生成树。生成树上的各边权的总和称为该树的耗费。在G的所有生成树中，耗费最小的生成树称为G的最小生成树。

Prim算法

template<class Type>
void Prim(int n,Type **c)
{
    Type lowcost[maxint];
    Type closest[maxint];
    bool s[maxint];
    s[1]=true;
    for(int i=2;i<=n;i++){
        lowcost[i]=c[1][i];
        closest[i]=1;
        s[1]=false;
    }
    for(int i=1;i<n;i++){
        Type min =inf;
        int j=1;
        for(int k=2;k<=n;k++){
            if((lowcost[k]<min)&&(!s[k])){
                min=lowcost[k];
                j=k;
            }
        }
    }
    cout << j << " " << closest[j] << endl;
    s[j]=true;
    for(int k=2;k<=n;k++){
        if((c[j][k]<lowcost[k])&&(!s[k])){
            lowcost[k]=c[j][k];
            closest[k]=j;
        }
    }
}

Kruskal算法

template<class Type>
bool Kruskal(int n,int e,EdgeNode<Type> E[],EdgeNode<Type> t[]){
    MinHeap<EdgeNode<Type>H(1);
    H.Initialize(E,e,e);
    UnionFind U(n);
    int k=0;
    while(e&&k<n-1){
        EdgeNode<int> x;
        H.DeleteMin(x);
        e--;
        int a=U.Find(x.u);
        int b=U.Find(x,v);
        if(a!=b){
            t[k++]=x;
            U.Union(a,b);
        }
        H.Deactivate();
        return (k==n-1);
    }
}

多机调度问题

问题描述：设有n各独立的作业{1,2,…,n}，由m台相同的机器进行加工处理。作业i所需的处理时间为ti。多机调度问题要求给出一种作业调度方案，使得所给的n个作业在尽可能短的时间内由m台机器加工处理完成。

算法思想：采用最长处理时间作业优先的贪心选择策略，可以设计出解多级调度问题的较好的近似算法。按此策略，当n<=m时，只要将机器i的[0.ti]时间区间分配个作业i即可。当n>m时，先将n个作业依其所需的处理时间从大到小排序，再依次顺序将作业分配给空闲的机器。

今天的文章算法设计与分析第四章课后答案_关于计算机体系结构的思维导图分享到此就结束了，感谢您的阅读。