【计组】简单理解集中式刷新、分散式刷新、异步式刷新

引子

角色

先来看看这三种刷新中的两个角色…

存储单元：存数据的小弟，一行为一个单位（假设存储器有256行，每行有256列），这里有256行存储单元，这些孩子编号为0~255行————一次操作一行的存储单元~
cpu：老大哥。从存储单元里面操作数据啦，一次取一行或者写一行的数据。

那么他们要做什么呢?自然是老大哥(cpu)想让小弟们(一行一行的存储单元)存或者写数据啦~

访问和刷新时…

但是，存储单元有一个特性：每隔一段时间得充电，也就是刷新，不然就会由于没电导致数据丢失（假设4ms内必须充电一次，这个4ms，也叫做最大刷新周期）。

那么，当cpu读取或者写入数据的时候，就会出现下面两种情况：

正常情况：【cpu】：我来读/写数据啦！【某行小弟】：好的老大，我现在有电！这就把数据给您…（时间过了一个存储周期）老大再见！！！常来玩！（当某一行不在充电/刷新时，正常读写）
死区：【cpu】：我来读/写数据啦！【某行小弟】：老大不好了！我可能快要没电了！，根据刷新规则！我得先充个电！等我先充个电去保护一下数据！！！老大过会再来呗！（当根据刷新规则，某一行进行刷新的这段时间，该行无法进行数据读写。此段用来刷新的时间称作死区）

一些特性

这里还得补充一点点：

cpu读/写数据是需要时间的，读/写一次所耗费的时间叫做存取周期（存储周期），同时我们假设存取周期为0.5us。
某一行充一次电/刷新一次的时间，也等于一个存取周期（存储周期）。
刷新间隔：所有存储单元都刷新一遍所需要的时间，也是两次所有存储单元开始刷新之间间隔的时间。

回过头来那么，上文的刷新规则是什么呢？

其实就是标题所指的三种刷新方式：集中式刷新、分散式刷新、异步式刷新。

集中式刷新

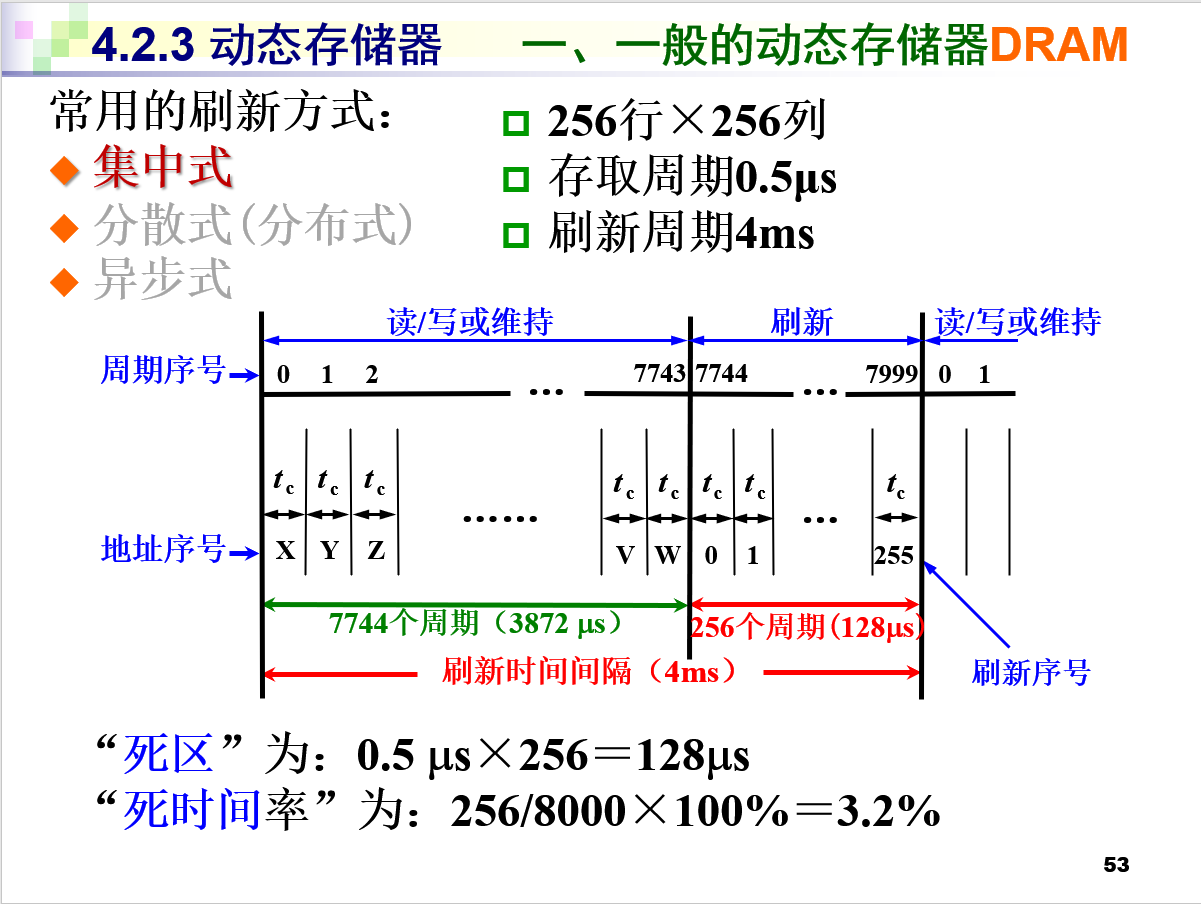
在一个刷新周期（4ms）内，所有的小弟们（存储单元行）约好了一起去刷新，由于一次只能刷新一行，一行刷新花费0.5us，故所有行一共花费256×0.5us的时间集中在一起去刷新（充电）

大概是这种感觉：
每4ms（4000us=8000个周期）中：
前7744个周期（3872us）cpu：正常的要求读写，存储单元们：正常的读写
后256个周期（0.5us*256=128us=256个周期）cpu：人呢？存储单元们：排队充电呢！（一行一行的排队，一行为一个单位）

前7744个周期就是正常的读/写或者维持周期，对应着上面“正常”的情况，后256个周期就是刷新周期，也就是死区，对应着上文“死区”的情况。

分散式刷新

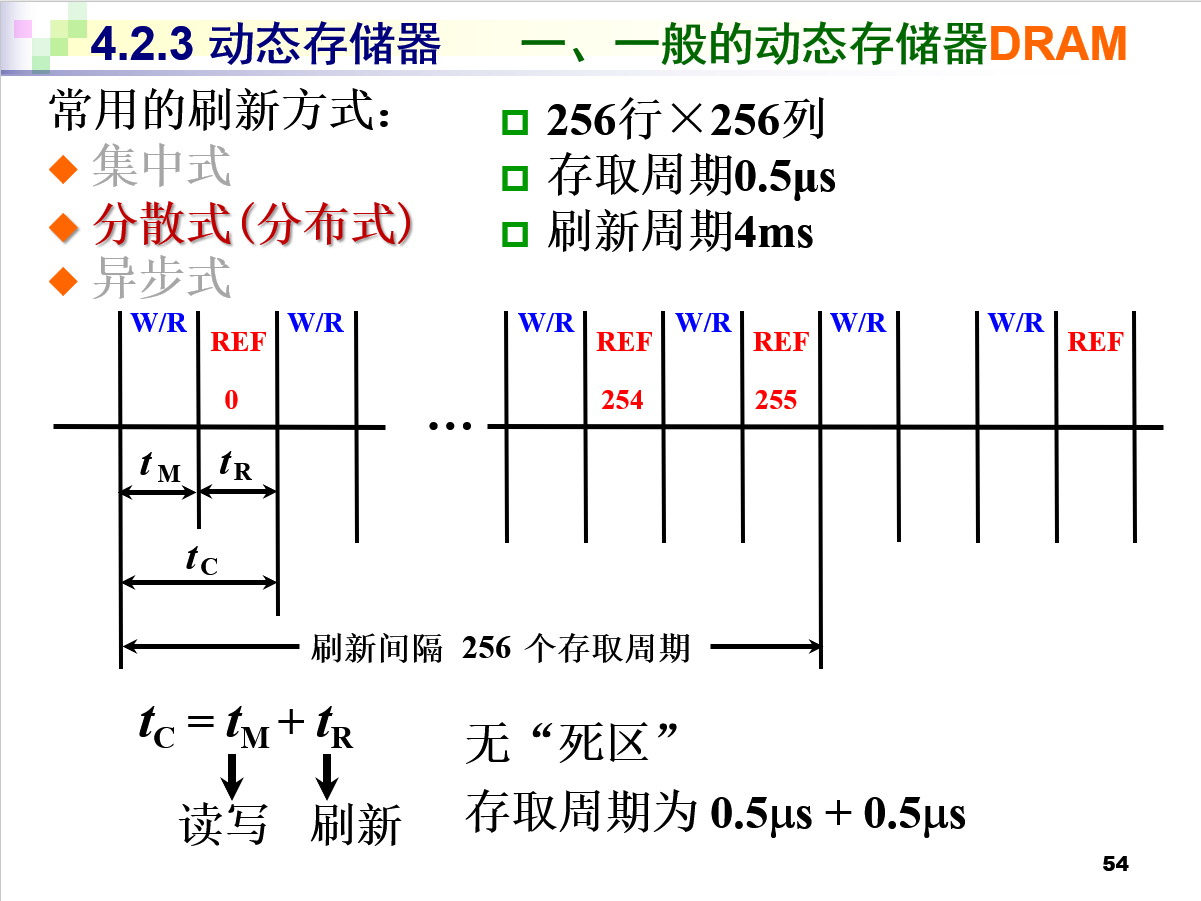
每读取一次，某一行就刷新一次

每次cpu去读写某一行的时候，读完了，还没完事，还得等这一行刷新完成之后，才算完整的完成了一次存取周期。

这样悄悄的把刷新的时间融入到存取周期中，也就不存在单独用来刷新的时间了。

因为刷新时间就是死区，那么没有刷新时间就没有死区，所以分散式刷新不存在死区。

代价就是，由于把刷新时间融入到了存取周期中，导致存取T周期变长：Tc(新的存取周期)=Tm(原来的存取周期)+Tr(每一个周期完成一次存取之后立刻刷新)=0.5us+0.5ms=1us。所以整体的存取周期变长了，实际存取的效率也就下降了，虽然没有了死区。

打个比方，假如刷新就是摸鱼。
原来是：集中摸鱼，摸鱼这段时间不跟cpu工作（死区）。
现在是：看似不摸鱼了，所有时间都可以跟cpu工作（无死区），但是原来0.5us能干完的读写操作现在非得花1us才做完，这1us中实际上悄悄的摸鱼了0.5us（1us中有0.5ms用于刷新）

如此一来，倘若每次cpu都读写不同的行，则每隔256个1us的存取周期（256*（0.5+0.5））所有的行都可刷新一次，则任意一行的刷新间隔为256个存取周期，整体的刷新间隔（所有行都被刷新一次）的刷新间隔也为256个存取周期。

有的同学会问，这里分散刷新是只有读写操作的时候才刷新，如果某一行一直没有被cpu读写，或者cpu一直读写某一行？那是不是就会造成数据的丢失？

先说确定的结论：大家大可不必担心这个问题，因为“无关紧要”，只需要了解分散式刷新的原理以及“每次都应该会读写不同的行，存取周期加倍，刷新间隔是行数个周期”即可。

再说笔者的瞎掰愚见：提出这个问题的童鞋一定是非常善于思考的。这个问题的实质在我看来就和：为什么牛顿经典力学在微观中不适用但是在宏观中适用？原子内部有间隔甚至按照某些理论是按照概率在空间中出现，那么我是由很多原子构成的，是不是一直持续用力的撞墙也有概率“穿墙”？

这种问题有一些相同的特点：我们用微观的思考方式去考虑宏观的问题。为了大家理解“分散刷新”，所有的资料书或者教材都用微观且理想的一块存储器来举例子，并且告诉大家在微观当中发生了什么。但是在宏观中，如同“会不会一直读取某一行”或者“会不会一直不读某一行”这种在微观中有可能发生的事情发生的情况，就如同“在微观中原子确实有概率穿墙但在宏观中我们一直在撞墙”的情况一样，虽然确实在微观的角度下会发生，但是在一个实际的分散刷新的存储器中，以宏观视角来看，这样的事件也同理几乎不会发生。再用概率的视角来看，每一行被读/写的概率几乎相同，若把时间扩展到足够长，读取次数足够多（即从宏观的视角），每一行被读取的次数几乎是相同的，那么平均来看，从微观来看，我们也可以近似的看成cpu每一次都读/写了不同行。

当然有兴趣我觉得最好还是实际找一块真真实实的分散式刷新的存储芯片，实际看一看到底真实情况下分散刷新如何工作的，可能可以更好的回答这个问题。

异步式刷新

每一行只要在最大刷新周期（不刷新/充电就丢失数据的极限时间）内，找个每一行它自己觉得方便的时候刷新即可。

但是每次存储单元只能刷新一行，那么最多多久时间就必须刷新一行？从而保证每一行能在最大刷新周期内被刷新？

假设最大刷新周期为4ms，有256行且每一行必须在4ms内被刷新。

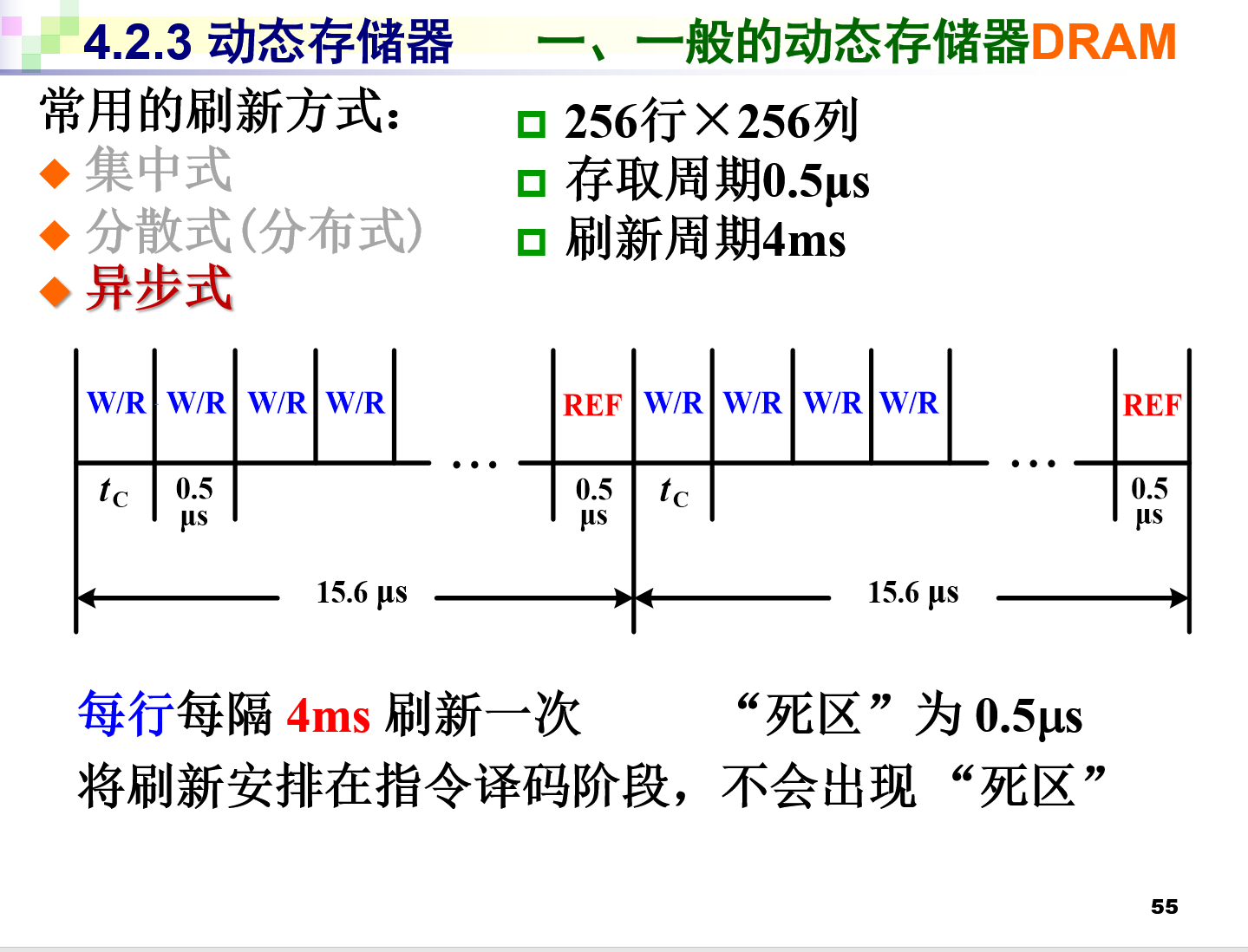
那么每隔4(ms)/256(行)=15.6(us/行)的时间就必须刷新一行（这个时间内任选0.5us来刷新），才能保证在一个最大刷新周期内，每一行都被刷新。

可能有些数感不太好的同学（比如笔者），在这里会有点晕。我们来验证一下，如果某一行在某一轮被刷新了，那么在给接下来的255轮刷新时（每一轮刷新一行），它都不会刷新（每一轮在刷新别的行呢！），它下一次刷新是在15.6us/行*255行之后，它要等256轮才会失去信息，所以就保证了数据的不丢失。

请看图：

可能有的同学还有点晕，不知道这个15.6us是什么东西。15.6us是刷新一行最多允许间隔的时间，换个说法，就是每隔15.6us必须刷新一行， ~~更容易混淆的说法叫做(存储器)每次刷新周期（间隔）~~ 。因为从前面的计算不难看出，只有至少每15.6u刷新一行，才能保证在4ms这个极限刷新时间内，所有的行都被刷新，才能保证在每次刷新不同行的时候，每两行之间间隔的时间小于4ms。