MATLAB学习笔记（一）常值函数与跳变函数的绘制「建议收藏」

MATLAB学习笔记（一）常值函数与跳变函数的绘制

1.常值函数

比如，我们要绘 $f(x)=5,x\in \left(0,10\right)$ 的函数图，我们知道他是一条平行于x轴的直线，一般人想的代码可能是：（这是错误的）

x = 0: 10;
y = 5;
plot(x,y)

正确的应该这样书写：

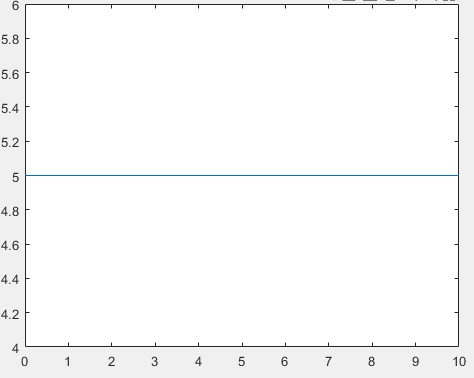
x = [0,10];
y = [5,5];
plot(x,y)

他的意思是在$x=0$处函数值为5，$x=10$处函数值为5，连接$\left(0,5\right)$和$\left(10,5\right)$两个点从而形成一条直线。

2.跳变函数

在绘制一些跃变函数的时候，间断点处有实线了，原因是：虽然函数值在此处发生了突变，但是在该间断点处是有值的，举个例子，信号与系统中常等效为开关的单位阶跃函数：
$$f(x)=\{\begin{array}{r}0,x<0\\ 1,x\ge 0\end{array}\text{\hspace{1em}(2.3)}$$
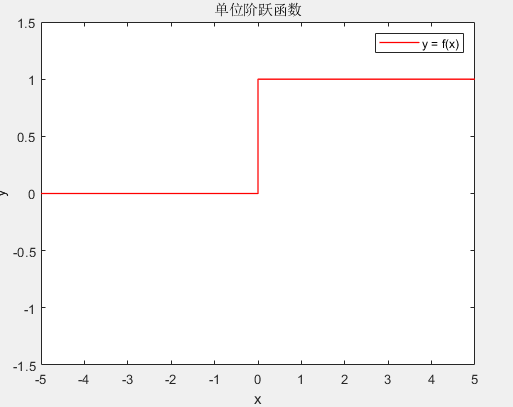
用第一节中绘制常值函数的方法，在$x=0$处取两个点$\left(0,0\right)$和$\left(0,1\right)$，这样就可以补充出阶跃的这条线了，代码如下：

x = [-5,0,0,5];
y = [0,0,1,1];
plot(x,y,'r','linewidth',1.0);

legend('y = f(x)'); %可依次设置成你想要的名字
xlabel('x');
ylabel('y');
title('单位阶跃函数')
axis([-5 5  -1.5 1.5]);

今天的文章MATLAB学习笔记（一）常值函数与跳变函数的绘制「建议收藏」分享到此就结束了，感谢您的阅读。