spss分析方法-因子分析（转载）

因子分析就是将大量的彼此可能存在相关关系的变量，转换成较少的彼此不相关的综合指标的多元统计方法。。
下面我们主要从下面四个方面来解说：
 

• 实际应用
• 理论思想
• 建立模型
   
• 分析结果

一、实际应用

在市场调研中，研究人员关心的是一些研究指标的集成或者组合，这些概念通常是通过等级评分问题来测量的，如利用李克特量表取得的变量。每一个指标的集合（或一组相关联的指标）就是一个因子，指标概念等级得分就是因子得分。
因子分析在市场调研中有着广泛的应用，主要包括：
（1）消费者习惯和态度研究（U&A）
（2） 品牌形象和特性研究
（3）服务质量调查
（4） 个性测试
（5）形象调查
（6） 市场划分识别
（7）顾客、产品和行为分类在实际应用中，通过因子得分可以得出不同因子的重要性指标，而管理者则可根据这些指标的重要性来决定首先要解决的市场问题或产品问题。

二、理论思想

因子分析（Factor Analysis）是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系，探求观测数据中的基本结构，并用少数几个独立的不可观测变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显式变量，而假想变量是不可观测的潜在变量，称为因子。
主成分分析利用的是“降维”的思想，利用原始变量的线性组合组成主成分。在信息损失较小的前提下，把多个指标转化为几个互补相关的综合指标。
因子分析是主成分分析的扩展和推广，通过对原始变量的相关系数矩阵内部结构的研究，导出能控制所有变量的少数几个不可观测的综合变量，通过这少数几个综合变量去描述原始的多个变量之间的相关关系。。

因子分析的数学模型可以表示为Xp×1=Ap×m·Fm×1+ep×1，其中X为可实测的p维随机向量，它的每个分量代表一个指标或变量。

F=(F1, F2,…,Fm)T为不可观测的m维随机向量，它的各个分量将出现在每个变量之中，所以称它们为公共因子。矩阵A称为因子载荷矩阵，矩阵中的每一个元素称为因子载荷，表示第i个变量在第j个公共因子上的载荷，它们需要由多次观测X所得到的样本来估计。

向量e称为特殊因子，其中包括随机误差，它们满足条件：

（1）Cov(F,e)=0，即F与e不相关。

（2）Cov(Fi,Fj)=0,i≠j ，Var(Fi)=Cov(Fi, Fj)=I ，即向量F的协方差矩阵为m阶单位阵。（

3）Cov(ei,ej)=0,i≠j ，Var(ei)=σi2，即向量e的协方差矩阵为p阶对角阵。因子分析的基本思想是通过变量的相关系数矩阵内部结构的分析，从中找出少数几个能控制原始变量的随机变量Fi(i=1,2,…,m)，选取公共因子的原则是使尽可能多地包含原始变量中的信息，建立模型X=A· F+e ，忽略e，以F代替X，用它再现原始变量X的众多分量之间的相关关系，达到简化变量降低维数的目的。

三、建立模型

因子分析的基本步骤如下。

• 对数据进行标准化处理，
• 估计因子载荷矩阵，
• 因子旋转，建立因子分析数学模型的目的不仅要找出公共因子并对变量进行分组，更重要的是要知道每个公共因子的意义，以便对实际问题作出科学分析。当因子载荷矩阵A的结构不便对主因子进行解释时，可用一个正交阵右乘A（即对A实施一个正交变换）。由线性代数知识，对A施行一个正交变换，对应坐标系就有一次旋转，便于对因子的意义进行解释。
• 估计因子得分以公共因子表示原因变量的线性组合，而得到因子得分函数。我们可以通过因子得分函数计算观测记录在各个公共因子上的得分，从而解决公共因子不可观测的问题。
   

因子分析案例：
 

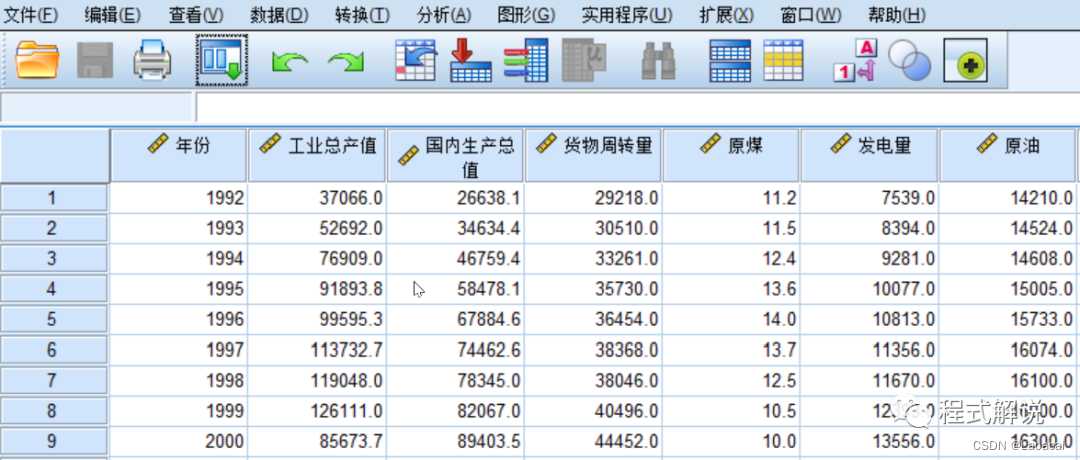
题目：以下给出了中国历年国民经济主要指标统计（1992～2000）数据。试用因子分析对这些指标提取公因子并写出提取的公因子与这些指标之间的表达式。

一、数据输入

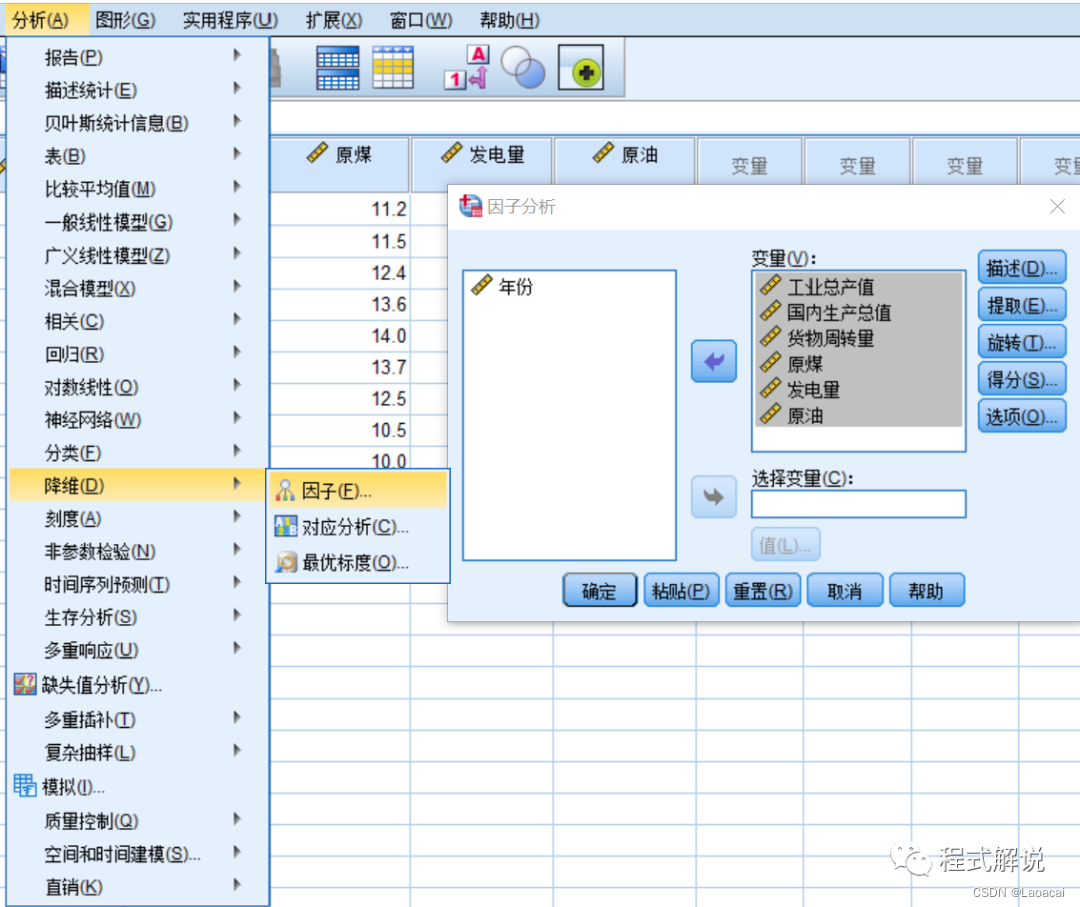
二、操作步骤1、进入SPSS，打开相关数据文件，选择“分析”|“降维”|“因子”命令。2、选择进行因子分析的变量。在对话框的左侧列表框中，依次选择“工业总产值”“国内生产总值”“货物周转量”“原煤”“发电量”“原油”进入“变量”列表框。

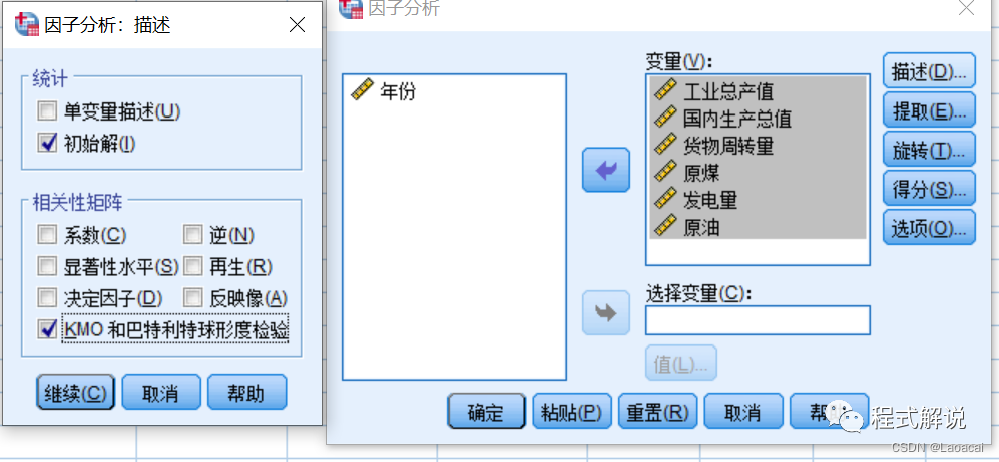
3、选择输出系数相关矩阵。

单击“因子分析”对话框中的“描述”按钮，弹出“因子分析：描述”对话框。在“相关性矩阵”选项组中选中“KMO和巴特利特的球形度检验”复选框，单击“继续”按钮返回“因子分析”对话框。

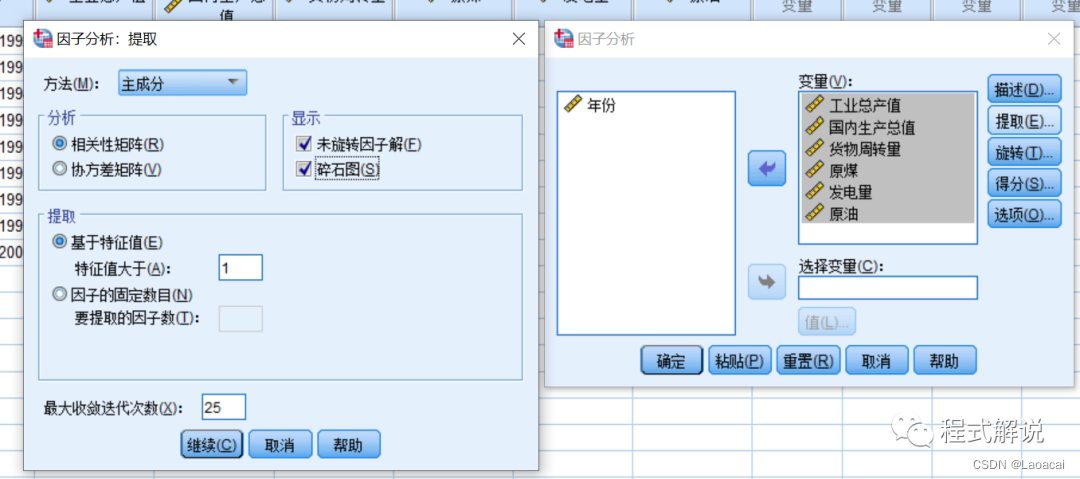
4、设置对提取公因子的要求及相关输出内容。

单击“因子分析”对话框中的“提取”按钮，在“输出”选项组中选中“碎石图”复选框。

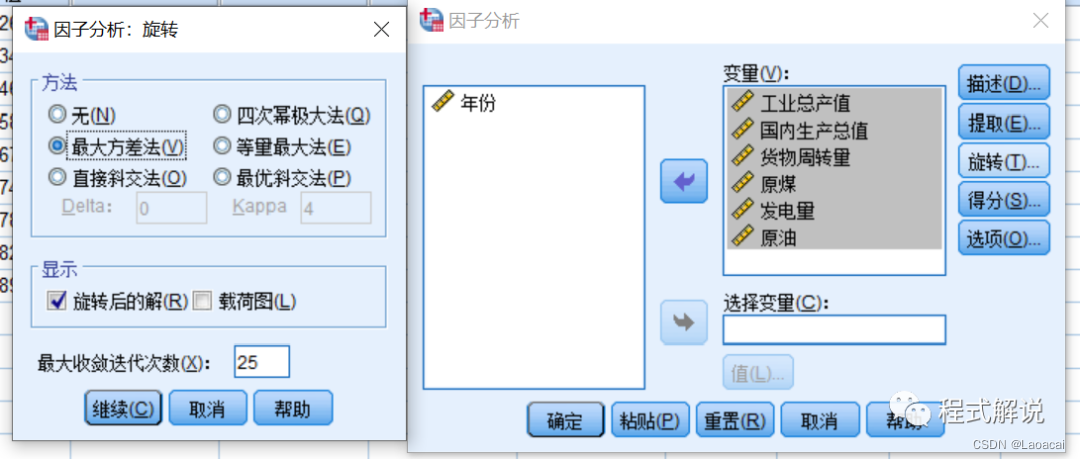
5、设置因子旋转方法。单击“因子分析”对话框中的“旋转”按钮，在“方法”选项组中选中“最大方差法”单选按钮。

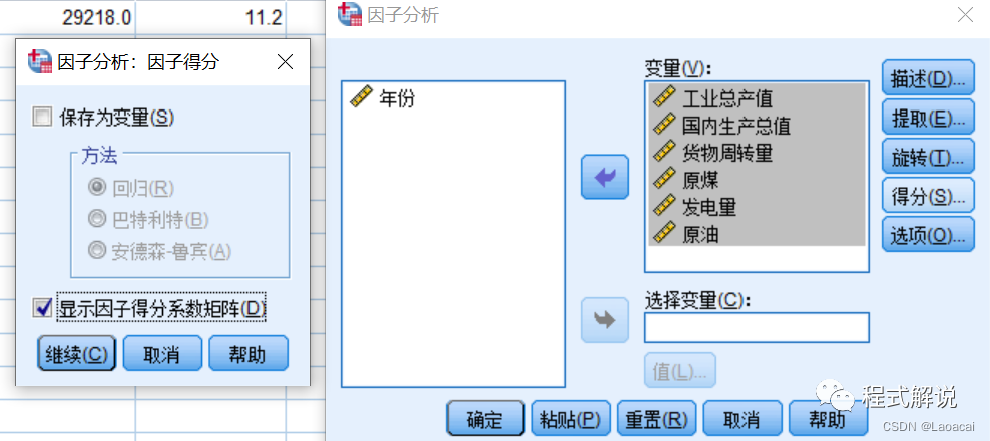
6、设置有关因子得分的选项。单击“得分”按钮，选中“显示因子得分系数矩阵”复选框。

7、其余设置采用系统默认值即可。单击“确定”按钮，等待输出结果。

四、结果分析

1、KMO检验和巴特利特检验结果KMO检验是为了看数据是否适合进行因子分析，其取值范围是0～1。其中0.9～1表示极好，0.8～0.9表示可奖励的，0.7～0.8表示还好，0.6～0.7表示中等，0.5～0.6表示糟糕，0～0.5表示不可接受。如下表所示，本例中KMO的取值为0.657，表明可以进行因子分析。巴特利特检验是为了看数据是否来自于服从多元正态分布的总体。本例中显著性值为0.000，说明数据来自正态分布总体，适合进一步分析。

2、变量共同度变量共同度表示的是各变量中所含原始信息能被提取的公因子所解释的程度。如下表所示，因为本例中所有变量共同度都在85%以上，所以提取的这几个公因子对各变量的解释能力很强。

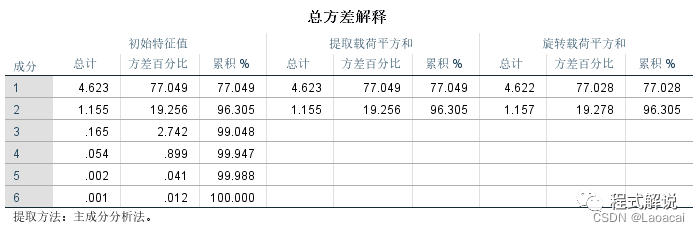
3、解释的总方差由下表可知，“初始特征值”一列显示只有前两个特征值大于1，所以SPSS只选择了前两个主成分；“提取载荷平方和”一列显示第一主成分的方差贡献率是77.049%，前两个主成分的方差占所有主成分方差的96.305%，由此可见，选前两个主成分已足够替代原来的变量，几乎涵盖了原变量的全部信息；“旋转载荷平方和”一列显示的是旋转以后的因子提取结果，与未旋转之前差别不大。

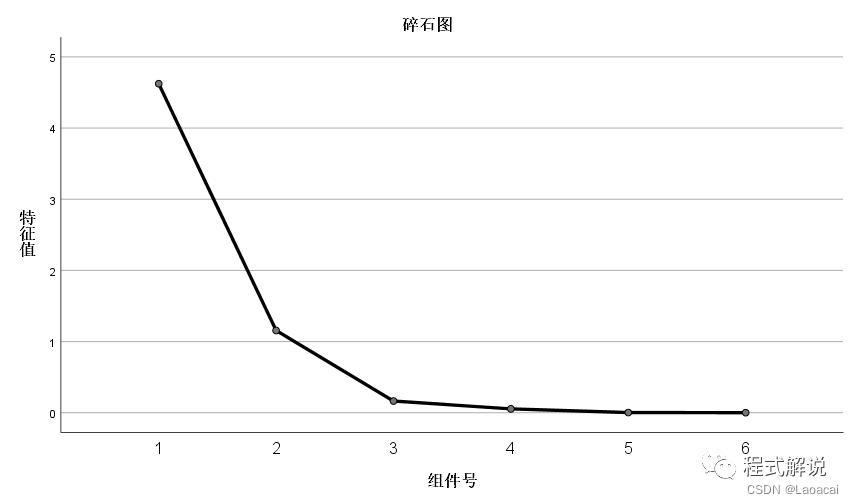
4、碎石图有两个成分的特征值超过了1，只考虑这两个成分即可。

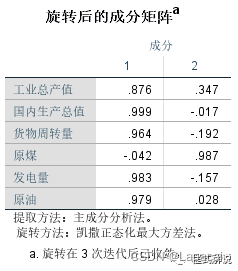
5、旋转成分矩阵第一个因子在工业总产值、国内生产总值、货物周转量、发电量及原油上有较大的载荷，所以其反映的是除原煤以外的其他变量的信息，第二个因子在原煤这一变量上有较大的载荷，反映的是原煤这一变量的信息。

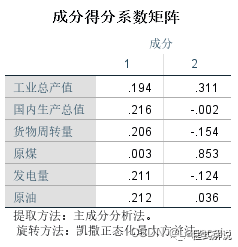
6、成分得分系数矩阵给出了成分得分系数矩阵，据此可以直接写出各公因子的表达式。值得一提的是，在表达式中各个变量已经不是原始变量而是标准化变量。表达式如下：F1=0.194*工业总产值+0.216*国内生产总值+0.206*货物周转量+0.003*原煤+0.211*发电量+0.212*原油F2=0.311*工业总产值-0.002*国内生产总值-0.154*货物周转量+0.853*原煤-0.124*发电量+0.036*原油

分析结论：
 

通过分析，我们可以知道：

由结果分析1、知，本例很适合使用因子分析。

由结果分析2、3、4可知，本例适合选前两个公因子进行分析，因为这已足够替代原来的变量，它们几乎涵盖了原变量的全部信息。

结果分析5给出了本例中的两个公因子及其所反映的变量。

结果分析6给出了公因子与标准化形式的变量之间的表达式。

参考案例数据：
 

1. spss统计分析与行业应用案例详解(第四版)  杨维忠,张甜,王国平  清华大学出版社
2. （获取更多知识，前往gz号程式解说）

原文来自https://mp.weixin.qq.com/s/5b-rkSherOn-tHyzBZPsTw

今天的文章spss分析方法-因子分析（转载）分享到此就结束了，感谢您的阅读。