常用的相关分析系数
相关分析是衡量事物之间或称变量之间线性相关程度的强弱,并用适当的统计指标表示出来的过程。比如,家庭收入和支出、一个人所受教育程度与其收入、子女身高和父母身高等。
相关分析的计算方式有三种,分别是Pearson相关系数(适用于定量数据,且数据满足正态分布)、Spearman相关系数(数据不满足正态分布时使用)。Kendall’s tau -b相关系数(有序定类变量)。
一、Spearman Rank相关系数
1.1 Pearson相关系数的定义
- 当两个变量都是正态连续独立变量,而且两者之间呈线性关系,两变量的方差不为0,通常用Pearson相关系数来衡量。
pearson是一个介于-1和1之间的值,当两个变量的线性关系增强时,相关系数趋于1或-1;当一个变量增大,另一个变量也增大时,表明它们之间是正相关的,相关系数大于0;如果一个变量增大,另一个变量却减小,表明它们之间是负相关的,相关系数小于0;如果相关系数等于0,表明它们之间不存在线性相关关系。
ρ x , y = c o v ( x , y ) σ x σ y = E [ ( x − μ x ) ( y − μ y ) ] σ x σ y \rho_{x,y}=\frac{cov(x,y)}{\sigma_x\sigma_y}=\frac{E[(x-\mu_x)(y-\mu_y)]}{\sigma_x\sigma_y} ρx,y=σxσycov(x,y)=σxσyE[(x−μx)(y−μy)]
上式定义了总体相关系数,常用希腊小写字母 ρ 作为代表符号。估算样本的协方差和标准差,可得到样本 Pearson 相关系数,用英文小写字母 r 表示
r x , y = ∑ i = 1 n ( x i − x ˉ ) ( y i − x ˉ ) ∑ i = 1 n ( x i − x ˉ ) ∑ i = 1 n ( y i − y ˉ ) r_{x,y}=\frac{\sum_{i=1}^n(x_i – \bar{x})(y_i-\bar{x})}{\sqrt {\sum_{i=1}^n(x_i – \bar{x})}\sqrt {\sum_{i=1}^n(y_i – \bar{y})}} rx,y=∑i=1n(xi−xˉ)∑i=1n(yi−yˉ)∑i=1n(xi−xˉ)(yi−xˉ)
显著性检验的统计量为t统计量,其数学定义为:
t ( n − 2 ) = r n − 2 1 − r 2 t(n-2) = \frac{r\sqrt{n-2}}{\sqrt{1-r^2}} t(n−2)=1−r2rn−2
虽然协方差 c o v ( x , y ) = ∑ i = 1 n ( x i − x ˉ ) ( y − y ˉ ) n − 1 cov(x,y)=\frac{\sum_{i=1}^n(x_i-\bar{x})(y-\bar{y})}{n-1} cov(x,y)=n−1∑i=1n(xi−xˉ)(y−yˉ)能反映两个随机变量的相关程度(协方差大于0的时候表示两者正相关,小于0的时候表示两者负相关),但是协方差值的大小并不能很好地度量两个随机变量的关联程度。
在二维空间中分布着一些数据,我们想知道数据点坐标X轴和Y轴的相关程度,如果X与Y的相关程度较小但是数据分布的比较离散,这样会导致求出的协方差值较大,用这个值来度量相关程度是不合理的,为了更好的度量两个随机变量的相关程度,引入了Pearson相关系数,其在协方差的基础上除以了两个随机变量的标准差。
- Pearson 相关系数对异常值比较敏感,在数据清洗阶段需要将异常值过滤或者平滑处理。
1.2 python实现pearson相关系数
import numpy as np
import scipy.stats as stats
import scipy
# 某银行25家分行不良贷款(y)与贷款余额(x)如下:
x = [67.3,111.3,173,80.8,199.7,16.2,107.4,185.4,96.1,72.8,64.2,132.2,58.6,174.6,263.5,79.3,14.8,73.5,24.7,139.4,368.2,95.7,109.6,196.2,102.2]
y = [0.9,1.1,4.8,3.2,7.8,2.7,1.6,12.5,1.0,2.6,0.3,4,0.8,3.5,10.2,3,0.2,0.4,1,6.8,11.6,1.6,1.2,7.2,3.2]
correlation,pvalue = stats.stats.pearsonr(x,y)
print ('correlation',correlation)
print ('pvalue',pvalue)
二、Spearman秩相关系数
2.1 Spearman 秩相关系数的定义
Spearman Rank相关系数,即斯皮尔曼秩相关系数(Spearman Rank Order Correlation Coefficient,简称SROCC)。
Spearman 秩相关系数是一个非参数性质(与分布无关、与是否线性关系无关)的秩统计参数,是用来度量两个连续型变量之间单调关系强弱的相关系数,取值范围也是 [−1,1],也可检测有序的离散变量间的相关系数.采用秩来计算,避免离群值对相关系数的影响。在没有重复数据的情况下,如果一个变量是另外一个变量的严格单调函数,则 Spearman 秩相关系数就是 1 或 −1,称变量完全 Spearman 秩相关。
秩相关 (Rank Correlation),又称等级相关,是将两变量的样本值按数据的大小顺序排列位次,以各要素样本值的位次代替实际数据而求得的一种统计量。排序不论从大到小还是从小到大排都无所谓,只要保证大家排序的标准一致即可。
用 ρ s ρ_s ρs 来表示 Spearman 相关系数 (用 ρ_p 表示 Pearson 相关系数)。如果每个变量都没有相同的取值 (即没有相同的秩次),则 Spearman 相关系数可由下式计算:
ρ s = 1 − 6 ∑ d i 2 n ( n 2 − 1 ) ρ_s=1−\frac{6\sum d_i^2}{n(n^2-1)} ρs=1−n(n2−1)6∑di2
其中,n 表示数据点的个数;di 表示数据点 ( x i , y i ) (x_i,y_i) (xi,yi)的秩次 ( r x i , r y i ) (r_{x_i},r_{y_i}) (rxi,ryi)之差: d i = r x i − r y i d_i=r_{x_i}-r_{y_i} di=rxi−ryi。
如果某个变量有重复数据,则计算变量之间的 Spearman 相关系数就是计算变量数据秩次之间的 Pearson 相关系数:
ρ s = ρ r x , r y = c o v ( r x , r y ) σ r x σ r y ρ_s=ρ_{r_x,r_y}=\frac{cov(r_x,r_y)}{\sigma _{r_x}\sigma _{r_y}} ρs=ρrx,ry=σrxσrycov(rx,ry)
其中,rx 表示变量 x 转换后的秩次。从这个定义可以看出来,Spearman 相关系数实际上就是对数据做了秩次变换后的 Pearson 相关系数。
此时,显著性检验的统计量为z统计量,其数据定义为:
Z = r n − 1 Z=r\sqrt{n-1} Z=rn−1
- 举例说明,首先将样本进行秩次变换,样本升序排列后的位次如表 所示:
| 编号 | x | y | r x r_x rx | r y r_y ry | d i = r x i − r y i d_i=r_{x_i}-r_{y_i} di=rxi−ryi |
|---|---|---|---|---|---|
| 1 | 0.1 | 0.1 | 1 | 1.5 | -0.5 |
| 2 | 0.2 | 0.1 | 2 | 1.5 | 0.5 |
| 3 | 0.3 | 0.2 | 3 | 3 | 0 |
| 4 | 0.4 | 0.6 | 4 | 4 | 0 |
| 5 | 0.5 | 0.7 | 5 | 5 | 0 |
| 6 | 0.6 | 0.8 | 6 | 6 | 0 |
| 7 | 0.7 | 0.9 | 7 | 7 | 0 |
| 8 | 0.8 | 1 | 8 | 8 | 0 |
需要说明的是,这里变量 y 有两个重复数据 0.1,在排序的时候它们的位次相同,此时可以用相同位次的数据所占的位次之和除以数据的数量 (即 (1+2)/2=1.5) 来作为这些重复数据的位次。
根据定义,当存在重复数据的时候,我们计算秩次 (即 rx, ry) 的 Pearson 相关系数
2.2 python 实现 Spearman 秩相关系数
from scipy.stats import spearmanr, pearsonr
x=[0.1, 0.2, 0.3, 0.4, 0.6, 0.7, 0.8, 0.9]
y=[0.1, 0.1, 0.2, 0.6, 0.7, 0.8, 0.9, 1.0]
spearmanr(x,y)
(0.99402979738800479, 5.2961535156451228e-07)
rx=[1, 2, 3, 4, 5, 6, 7, 8]
ry=[1.5, 1.5, 3, 4, 5, 6, 7, 8]
pearsonr(rx,ry)
- Spearman 相关系数是度量两个连续型变量之间单调关系强弱的相关系数,它对数据的分布不作任何假设,能够容忍异常值,也不需要数据的取值是等距的;
- Spearman 相关系数实际上就是对数据做了秩次变换后的 Pearson 相关系数,只要能用 Pearson 相关系数的地方就能使用 Spearman 相关系数;
- Spearman 相关系数还需要对原始数据进行排序,因此计算复杂度高于 Pearson 相关系数,当数据满足 Pearson 相关系数的使用条件时,优先考虑使用 Pearson 相关系数。
https://guyuecanhui.github.io/2019/07/28/feature-selection-spearman/
三、Kendall(肯德尔)秩相关系数
Kendall Rank相关系数,即肯德尔秩相关系数(KROCC),常用希腊字母τ(tau)表示。是一个非参数性质(与分布无关)的秩统计参数,是用来度量两个有序变量(如文化程度与消费比率的关系)之间单调关系强弱的相关系数。与Spearman秩相关系数基本类似。
Kendal秩相关系数公式有三个:
- τa公式适用于数据集中不存在相同数值的情况(即秩是唯一的)
k e n d a l τ a = c − d 1 2 n ( n − 1 ) = c − d c + d kendal \ \tau_a = \frac{c-d}{\frac{1}{2}n(n-1)}= \frac{c-d}{c+d} kendal τa=21n(n−1)c−d=c+dc−d
其中, m = 1 2 n ( n − 1 ) m={\frac{1}{2}n(n-1)} m=21n(n−1)表示所有样本两两组合的数量,在变量没有重复值的情况下,m=c+d。同序对c,就是两个变量取值的相对关系一致;异序对d:是指它们的相对关系不一致.
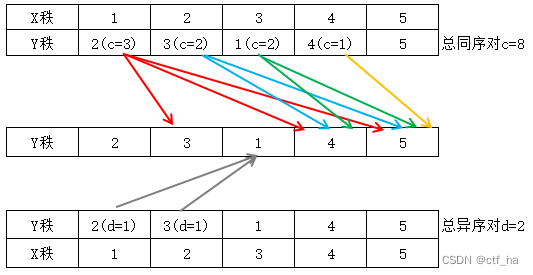
如下所示,假定变量X和变量Y的秩如下,先将X秩按升序排序,然后观察Y秩,变量Y的秩随变量X的秩同步增大的Y的秩对有(2,3),(2,4),(2,5),(3,4),(3,5),(1,4),(1,5),(4,5),即同序对的数目c共有8对;而变量Y的秩未随变量X的秩同步增大的Y的秩对有(2,1),(3,1),即异序对d共有2对。
- τb适用于存在相同数值的情况(即秩有重复的)
k e n d a l τ b = = ( c − d ) ( c + d + t x ) ( c + d + t y ) kendal \ \tau_b = = \frac{(c-d)}{\sqrt {(c+d+t_x)(c+d+t_y)}} kendal τb==(c+d+tx)(c+d+ty)(c−d)
其中,c 在计算的时候只能算 ai<aj 且 bi<bj 的对数,d 也只能算 ai<aj 且 bi>bj 的对数 (i<j);tx,ty 分别表示变量 x,y 取值中序号相同的样本对数排除共同平局的部分。
举例说明
- τc公式没有考虑相同数值带来的影响,适用于用表格表示的两变量间相关系数的计算
k e n d a l τ c = = 2 ∗ ( c − d ) n 2 m − 1 m kendal \ \tau_c = = \frac{2*(c-d)}{n^2\frac{m-1}{m}} kendal τc==n2mm−12∗(c−d)
其中 m = n ⋅ ( n − 1 ) 2 m=\frac{n\cdot (n-1)}{2} m=2n⋅(n−1)
Kendall检验是一个无参数假设检验,使用计算而得的相关系数去检验两个变量的相关显著性,其显著性检验的统计量为Z统计量,其数学定义为
Z = τ ∗ 9 n ( n − 1 ) 2 ( 2 n + 5 ) Z=\tau*\sqrt{\frac{9n(n-1)}{2(2n+5)}} Z=τ∗2(2n+5)9n(n−1)
from scipy.stats import kendalltau
kendalltau(x,y)
今天的文章pearson相关分析法spss_统计需求分析方法以为基础分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/86377.html