复变函数——学习笔记3：初等解析函数「建议收藏」

指数函数

定义3.1 对复数$z=x+iy$，定义：$e^z=e^x(\cos y+i\sin y)$

注意：以上的$e^z$并不是$e$的$z$次幂，而是一个记号，如果$z$是实数，那么其定义是实数的指数一致，如果$z$是纯虚数，$e^z=\cos y+i\sin y$就恰好为欧拉公式，对于$z=x+yi$，则$$|e^z|=e^x,Arg{e}^z=y+2k\pi$$

也就是说，对于直线$z(t)=x_0+it(-\infty <t<\infty )$，$w=e^z$将$z(t)$映射为$w$平面上的一个半径为$e^{x_0}$，圆心为0的圆。对于直线$z(t)=t+i{y}_0$，$w=e^z$将$z(t)$映成$w$平面的一条射线。下面我们列举$w=e^z$的一些性质：

(1)$e^{z_1}.e^{z_2}=e^{z_1+z_2}$
(2)$w=e^z$是复平面上的解析函数，并且$(e^z{)}^{\prime }=e^z$
(3)$w=e^z$有基本周期$2ki$

首先，$e^{x+yi}=e^{x+(y+2\pi )i}$，故$2\pi i$是$e^z$的一个周期
其次，如果$T$也是$e^z$的周期，那么$$e^{z+T}=e^z$$从而$$e^{Re(e^{z+T})}=|e^{z+T}|=e^{Re(z)}=|e^z|$$故$$Re(z+T)=Re(z)+Re(T)=Re(z)$$于是$Re(T)=0$，并且$$\begin{gathered} \cos (Im(z+T))=\cos (Im(z)) \\ \sin (Im(z+T))=\sin (Im(z)) \end{gathered}$$于是$$Im(z+T)=Im(z)+Im(T)=Im(z)+2k\pi$$故$$Im(T)=2k\pi$$因此$$T=2k\pi i$$因此$e^z$的任意周期都是$2\pi i$的整数倍，从而$2\pi i$是基本周期

分出单值解析分支的方法

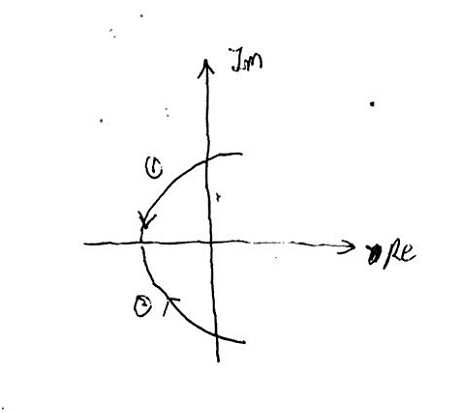
复数域存在大量的多值函数，幅角函数$\theta =Argz$就是其中之一，对于多值函数，我们需要分出单值分支。第一种方法是限制幅角函数的范围，如限制$-\pi <Argz\le \pi$，即限制$Argz$只能取主幅角，那么$\theta$在除去负半轴之外的区域上连续，而在负半轴上不连续。

如上图，从路线1逼近负半轴，幅角值趋近于$\pi$，从路线2逼近负半轴，幅角值趋近于$-\pi$。如果割破负半轴得到区域$G$，主幅角函数就在$G$上连续。
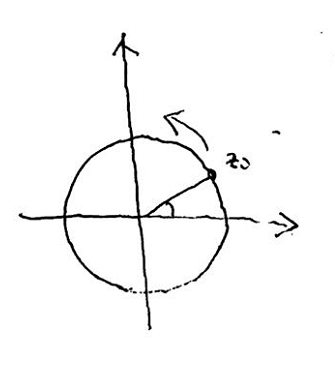
另一个分出单值分支的方法是取区域$G$内任意一点$z_0$，当然，$Arg{z}_0$是不止一个值，取定其中一个，对于$z$平面上的其他点$z^{\prime }$，我们作一条$z_0$到$z^{\prime }$的连续曲线，在动点$z$从$z_0$向$z^{\prime }$运动的过程中，$Argz$也随之连续变动，运动到$z^{\prime }$处$Argz$的值就是$z_0$处的幅角值。如此方法确定函数值会不会产生多值性呢？答案是肯定的，如果我们从$z_0$出发，绕着$0$逆时针环绕一周，幅角值连续变化，回到$z_0$时，幅角值将增加$2\pi$。如此一来，仅仅在$z_0$处，如此方式确定的函数值就有两个，见下图。

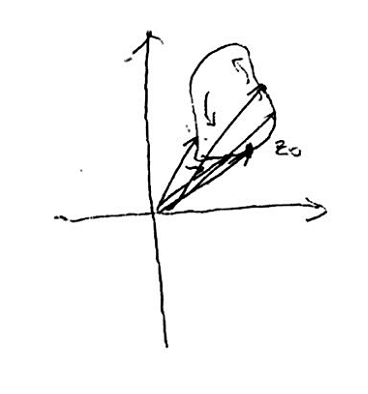
当然，如果我们在$z$平面上作一条闭曲线$C$，如果$C$不包含$0$，那么绕着$C$环绕一周，不论选取什么初始值，回到$z_0$点时，幅角值是不变的，如下图。

也就是说，无论作何闭曲线，只要闭曲线围成的区域不包含0，在$z_0$处取定幅角的某个初值$Arg{z}_0$，逆时针环绕一周，幅角连续变化，回到$z_0$时，幅角还是$Arg{z}_0$，可见$z=0$对于幅角函数来说，是一个很特殊点。如果$z_0$满足，绕着$z_0$作一个闭曲线$C$，$C$上取一点$z_1$，对于多值函数$f(z)$，取定某一个值$f(z_1)$，从$z_0$出发，绕着$C$逆时针转动，同时$f(z)$连续变化，回到$z_1$时，$f(z)$与初值不同，则称$z_0$是$f$的枝点。对于幅角函数来说$0$是支点，$\infty$也是支点，连接$0$和$\infty$（连接方式有很多，负半轴，甚至可以以曲线的方式连接），得到的连线称为支割线，只要不穿过这条线，闭曲线就永远不可能环绕0或环绕无穷，取定闭曲线某点的某个初值，在运动过程中幅角连续变动，回到原点时，函数值不变，用数学分析中线积分与路径无关的类似的方法，可以证明，如果在割除支割线后的区域上，任取一点$z_0$，选取某一个初值$f(z_0)$，对于另外一点$z$，从$z_0$连续变动至$z$，函数值也连续变动，可以唯一确定$f(z)$，这样就在去掉支割线的区域上分出一个连续的单值分支。如果我们割去负半轴，在$z=1$处取幅角的初值$0$，得到的单值分支就是$\arg z$。割去其他的支割线，得到的单值连续分支又是不同的。

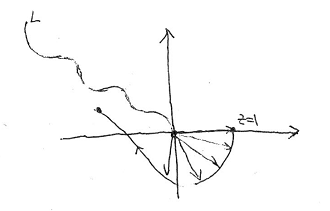
如上图，支割线如$L$所示，在$z=1$处取主值$Argz=0$，从$z=1$连续运动到第二象限的某点，可见得到的幅角值在$-\frac{3\pi }{2}$到$-\pi$之间，显然不是主幅角的值，这就很直观的可以看出，所作的支割线不同，得到的单值连续分支也不同。在支割线上，所得到的单值分支是不连续的，如果从上图所示的路径逼近支割线，得到的幅角值在$-\frac{3\pi }{2}$到$-\pi$之间，如果从第一象限到第二象限，从支割线上岸逼近支割线，得到的幅角值应该在$\frac{\pi }{2}$到$\pi$之间，故如此得到的单值连续分支在支割线上是间断的。

对数函数

定义3.2 对于复数$z\ne 0$，所有满足$e^w=z$的复数$w$称为$z$的对数，记为$Lnz$

显然$Lnz$也是个多值函数，如果对于$z=x+yi$，有$$z=e^{a+bi}=e^a(\cos b+i\sin b)$$就有$$\begin{gathered} |z|=e^a \\ Argz=b+2k\pi (k=0,\pm 1,\cdots ) \end{gathered}$$所以，选定$z$的某个幅角$Argz$，就有$$Lnz=\ln |z|+(Argz+2k\pi )i$$所以给定某个非零复数$z$，其对数值有无穷多个，对数函数是个多值函数，当然，幅角函数满足$$\begin{gathered} Arg(z_1{z}_2)=Arg(z_1)+Arg(z_2) \\ Arg(\frac{z_1}{z_2})=Arg(z_1)-Arg(z_2) \end{gathered}$$注意，以上两个式子的含义是，选定$z_1$的幅角值$Arg(z_1)$，$z_2$的幅角值$Arg(z_2)$，则$Arg(z_1)+Arg(z_2)$是$z_1{z}_2$的幅角值，复数相除时同理。因此，对于对数函数同样有$$\begin{gathered} Ln(z_1{z}_2)=Ln(z_1)+Ln(z_2) \\ Ln(\frac{z_1}{z_2})=Ln(z_1)-Ln(z_2) \end{gathered}$$直接验证即可证得以上两个等式，这和实数域上的对数函数的性质是类似的。接下来，我们来分出对数函数的单值分支。实际上，由表达式$$Lnz=\ln |z|+iArgz$$不难看出$Lnz$多值性产生的根源在于$z$的幅角函数的多值性，因此，我们可以通过限制$Argz$的范围来得到$Lnz$的单值分支，当然也可以通过割破$z$平面的方法得到单值分支。如果我们绕着$0$逆时针旋转一周，如绕着单位圆周$|z|=1$旋转一周，起点是$z=1$，初值选择$0$，当然此时$Argz=0$，逆时针旋转，同时$Argz$连续变动，当然，相对应地，$Lnz$也会相应地连续变动，运动一周回到$z=1$，$Lnz$变成了$2\pi i$。显然$0$和$\infty$是$Lnz$的支点，容易验证，除此之外没有支点，连接$0$和$\infty$就得到$Lnz$的支割线，取定某点的某个对数值，在不穿过支割线的情况下连续运动，相对应地$Argz$连续变动，相应地$Lnz$也会连续变动，运动到$z^{\prime }$时的对数值就是该分支的函数值。由此就得到分出$Lnz$的连续分支，假设除去支割线的区域为$D$，$Lnz$为$D$上的某个单值连续分支，则$$\begin{array}{rl}& \frac{Ln(z+\Delta z)-Ln(z)}{\Delta z}=\frac{Ln(z+\Delta z)-Ln(z)}{z+\Delta z-z}\\ =& \frac{Ln(z+\Delta z)-Ln(z)}{e^{Ln(z+\Delta z)}-e^{Ln(z)}}\end{array}$$当然，$Ln(z)$在该分支上是单射，因为两点要么模不同，要么幅角不同，因此$$\frac{Ln(z+\Delta z)-Ln(z)}{\Delta z}=\frac{1}{\frac{e^{Ln(z+\Delta z)}-e^{Ln(z)}}{Ln(z+\Delta z)-Ln(z)}}$$从而$$\underset{\Delta z\to 0}{\lim }\frac{Ln(z+\Delta z)-Ln(z)}{\Delta z}=\frac{1}{e^{Ln(z)}}=\frac{1}{z}$$因此，每一个$Ln(z)$的单值分支都解析，并且$(Ln(z){)}^{\prime }=\frac{1}{z}$

例3.1 在复平面上取上半虚轴作割线，试在所的区域内取$Lnz$在正实轴取实值的一个解析分支，并求它们在上半虚轴左沿的点及右沿的点$z=i$的值

解：
对于正实数$z=a$，$Lnz=\ln a+2k\pi i(k=0,\pm 1,\cdots )$，由于$Lnz$在正实轴上取实值，因此$k=0$，也就是说，在正实轴上$Argz=0$，再连续变动，$Lnz$相应地连续变动，就得到$Lnz$在割去上半虚轴后得到的区域的单值解析分支，表达式为$$Lnz=\ln |z|+iArgz$$其中$-\frac{3\pi }{2}<Argz<\frac{\pi }{2}$，在$z=i$处，$|z|=1$，从左边趋近得到的对数值是$-\frac{3\pi }{2}i$，从右边趋近得到的对数值为$\frac{\pi }{2}i$

幂函数

对于复数$\alpha$，定义幂函数为$z^{\alpha }=e^{\alpha Lnz}$，对不同的$\alpha$，我们来进行分类讨论：

(1) $\alpha$是有理数$\alpha =\frac{m}{n}$，其中$\frac{m}{n}$是既约分数$$z^{\alpha }=e^{\frac{m[ln|z|+(\arg z+2k\pi )i]}{n}}=|z{|}^{\frac{m}{n}}{e}^{\frac{m(\arg z+2k\pi )i}{n}}$$如果$n=1$，那么$z^{\alpha }$是单值函数
如果$n>1$，有$n$个不同的值，即上式取$k=0,1,\cdots ,n-1$¹
(2) 当$\alpha$是无理数时，$z^{\alpha }$有无穷多个值，即上式取$k=0,\pm 1,\pm 2,\cdots$²
(3)当$m$为纯虚数时，$z^{\alpha }$也取无穷个值，相同的办法可以验证，当$m$为虚部不为0的复数时，$z^{\alpha }$取无穷个值，即上式$k=0,\pm 1,\pm 2,\cdots$
(4)当$\alpha =\frac{1}{n}$时，$z^{\alpha }$记为$z$开$n$次方根

对于多值的幂函数，同样可以采用找出支点，作支割线的方法分出单值解析分支。
(1)取定某个$z\ne 0$，取定$z$的某个幅角值$Argz$，相应地，得到一个$z^{\alpha }$的值$e^{\alpha \ln |z|+i\alpha Argz}$，在连续变动的过程中，$Argz$连续变动，相应地$z^{\alpha }$也会连续变动，当$\alpha$不为整数时，容易验证$0$是$z^{\alpha }$的一个支点，相应地$\infty$也是$z^{\alpha }$的一个支点，除此之外没有支点，连接$0$和$\infty$就可以得到$z^{\alpha }$的支割线，相应地可以分出$z^{\alpha }$的解析分支，如果$\alpha$是有理数，$\alpha =\frac{m}{n}$(既约分数)，则可以分出$n$个不同的单值解析分支，当$\alpha$为无理数或虚部不为0的复数时，$z^{\alpha }$可以分出无穷个单值解析分支
(2)至于上面所说的解析性，可以将$z^{\alpha }$视为$e^z$和$mLnz$的复合，再用复合函数的求导法则可以证得，在每一个单值解析分支上，都有$$(z^{\alpha }{)}^{\prime }=\frac{\alpha }{z}{z}^{\alpha }$$

对于多项式$P(z)=z^n+a_1{z}^{n-1}+\cdots +a_{n-1}z+a_n(a_0\ne 0)$，下面我们讨论根式$$f(z)=\sqrt[m]{P(z)}$$的支点和单值解析分支，由代数基本定理，$P(z)$可因式分解为$$P(z)=(z-z_1{)}^{k_1}\cdots (z-z_s{)}^{k_s}$$其中$k_1+\cdots +k_s=n,k_i>0,z_1,\cdots ,z_s$为$P(z)$的两两不同的根，则$$\sqrt[m]{P(z)}=\sqrt[m]{|P(z)|}{e}^{\frac{{\sum }_{i=1}^s{k}_{i}Arg(z-z_i)}{m}}$$可见可能的支点为$z_1,\cdots ,z_s,\infty$，如何判断$z_1,\cdots ,z_s$是否为$f(z)$的支点，这是因为，绕着$z_1$的逆时针环绕一周（闭曲线$C$围成的区域不含$z_2,\cdots ,z_s$），在运动过程中$Arg(z-z_1),\cdots ,Arg(z-z_s)$均连续变动，$Arg(z-z_1)$获得增量$2\pi$，其余幅角不变，则$f(z)$变为初值乘以$e^{\frac{2k_1\pi }{m}i}$，如果$k_1$能被$m$整除，$z_1$是支点，否则不是，因为$e^{\frac{2k_1\pi }{m}i}=1$，环绕一周后$f(z)$还是初值。如果作一条闭曲线$C$，包含$z_1,\cdots ,z_i$$(i=1,\cdots ,s)$，而不含其它的根。逆时针运动一周，每个幅角连续变动，$\frac{{\sum }_{i=1}^s{k}_{i}Arg(z-z_i)}{m}$的改变量为$\frac{{\sum }_{j=1}^{i}2\pi k_j}{m}$，显然，如果${\sum }_{j=1}^i{k}_j$能被$m$整除，则环绕一周回到原值后函数值不变，否则函数值会发生改变。由此可以确定$\infty$是否是支点，并且还可以确定如何作支割线，下面给出几个实例：

例3.2 求函数$f(z)=\sqrt{(1-z^2)(1-k^2{z}^2)}(k>1)$的支点，作适当的支割线，将$f(z)$分成两个单值解析分支，并求在$z=0$取正值的那个分支

解：
$f(z)=\sqrt{|(1-z^2)(1-k^2{z}^2)|}{e}^{\frac{Arg(z-1)+Arg(z+1)+Arg(z-\frac{1}{k})+Arg(z+\frac{1}{k})}{2}i}$
显然$f(z)$可能的支点有五个$1,-1,\frac{1}{k},-\frac{1}{k},\infty$，对闭曲线$C$，容易验证，如果$C$只含$1,-1,\frac{1}{k},-\frac{1}{k}$中的某一点，那么逆时针环绕一周，$Arg(z-1)+Arg(z+1)+Arg(z-\frac{1}{k})+Arg(z+\frac{1}{k})$得到增量$2\pi$，故这四个点都是支点，如果绕着其中两个逆时针环绕一周，得到增量$4\pi$，环绕其中三个逆时针一周，得到增量$6\pi$，环绕四个逆时针一周得到增量$8\pi$，$\infty$不是支点，分别连接$-1,-\frac{1}{k}$和$\frac{1}{k},1$，就得到支割线，这样，任意闭曲线不可能只环绕四个点中的一个，也不可能环绕其中的三个，环绕一周后值不变，这样就得到$f(z)$的支割线，在$z=0$处，如果$Arg(z-1),Arg(z+1),Arg(z-\frac{1}{k}),Arg(z+\frac{1}{k})$都取主值，则$$Arg(z-1)+Arg(z+1)+Arg(z-\frac{1}{k})+Arg(z+\frac{1}{k})=2\pi$$则$f(z)$在$z=0$处取负值，因此，在$z=0$处，$$f(z)=\sqrt{|(1-z^2)(1-k^2{z}^2)|}{e}^{\frac{\arg (z-1)+\arg (z+1)+\arg (z-\frac{1}{k})+\arg (z+\frac{1}{k})}{2}i+\pi i}$$对于其他点，只要验证不穿过支割线的连续曲线运动，运动过程中$\arg (z-1),\arg (z+1),\arg (z-\frac{1}{k}),\arg (z+\frac{1}{k})$也连续变动，即可可导其他点的值，例如，如果我们要得到该分支在$z=i$处的值，沿着直线$z=ti(0\le t\le 1)$变动，$\arg (z-1),\arg (z+1),\arg (z-\frac{1}{k}),\arg (z+\frac{1}{k})$也连续变动，则$\arg (z+1),\arg (z+\frac{1}{k})$的幅角在增加，$\arg (z-1),\arg (z-\frac{1}{k})$在减小，但变动过程中始终保持$$\arg (z-1)+\arg (z+1)+\arg (z-\frac{1}{k})+\arg (z+\frac{1}{k})=2\pi$$见下图

在$z=i$处$$|(1-z^2)(1-k^2{z}^2)|=2(1+k^2)$$则在$z=i$处，$f(z)=\sqrt{2(1+k^2)}$

三角函数

由欧拉公式，对于实数$\theta$，有$$e^{\theta i}=\cos \theta +i\sin \theta$$就有$$\begin{gathered} e^{\theta i}+e^{-\theta i}=2\cos \theta \\ {e}^{\theta i}-e^{-\theta i}=2i\sin \theta \end{gathered}$$于是$$\begin{gathered} \cos \theta =\frac{e^{\theta i}+e^{-\theta i}}{2} \\ \sin \theta =\frac{e^{\theta i}-e^{-\theta i}}{2i} \end{gathered}$$这启发我们在复数域也可以如此定义三角函数，对于复数$z$，定义$$\begin{gathered} \cos z=\frac{e^{zi}+e^{-zi}}{2} \\ \sin z=\frac{e^{zi}-e^{-zi}}{2i} \end{gathered}$$如此定义的三角函数保持了实三角函数的一些性质：

(1)当$z$是实数时，$\sin z,\cos z$在实数域和复数域的定义一致
(2)$\sin z,\cos z$以$2\pi$为周期
(3)$\sin z$是奇函数，$\cos z$是偶函数
(4)$\sin (z_1+z_2)=\sin z_1\cos z_2+\cos z_1\sin z_2$
(5)$\cos (z_1+z_2)=\cos z_1\cos z_2-\sin z_1\sin z_2$
(6)$\sin z,\cos z$在复平面上解析，并且$$\begin{gathered} (\sin z{)}^{\prime }=\cos z \\ (\cos z{)}^{\prime }=-\sin z \end{gathered}$$(7)${\sin }^{2}z+{\cos }^{2}z=1$

实际上，(1)-(3)是显然的，我们下面逐个验证(4)-(7)：
(4)和(5)我们只验证(4)，(5)的验证是类似的：
$$\begin{gathered} \sin (z_1+z_2)=\frac{e^{i(z_1+z_2)-e^{-i(z_1+z_2)}}}{2i} \\ \sin z_1.\cos z_2=\frac{e^{i(z_1+z_2)}-e^{i(z_2-z_1)}+e^{i(z_1-z_2)}-e^{-i(z_1+z_2)}}{4i} \\ \cos z_1.\sin z_2=\frac{e^{i(z_1+z_2)}-e^{i(z_1-z_2)}+e^{i(z_2-z_1)}-e^{-i(z_1+z_2)}}{4i} \end{gathered}$$据此可以验证(4)等式左右两边相等
(6)则直接应用求导法则即可
(7)$$\begin{gathered} {\sin }^{2}z=\frac{e^{2iz}+2+e^{-2iz}}{4} \\ {\cos }^{2}z=\frac{e^{2iz}-2+e^{-2iz}}{-4} \end{gathered}$$故$${\sin }^z+{\cos }^z=1$$
但是在复数域，有些性质是不成立的，比如$|\sin z|\le 1,|\cos z|\le 1$。如果$\cos z\ne 0$，定义复数域的正切函数为$$\tan z=\frac{\sin z}{\cos z}$$同样，正切函数也解析，和实正切函数也有诸多类似的性质，这里就不一一列举了。

今天的文章复变函数——学习笔记3：初等解析函数「建议收藏」分享到此就结束了，感谢您的阅读。