广度优先搜索原理_深度优先算法时间复杂度

概述

        广度优先搜索（BFS）是一种重要的图遍历算法，用于在横向运动中搜索图的所有顶点。它从一个给定的顶点开始，在进入下一个级别之前访问它的所有邻居。BFS的时间复杂度取决于图中顶点和边的数量。

文章中使用的动画网站地址：
限 pc: 广度优先算法 ：http://www.donghuasuanfa.com/platform/portal?pc=bfs

算法一览表：https://blog.csdn.net/ww753951/article/details/106862328

动画算法一览表：http://www.donghuasuanfa.com/portal

算法过程

        算法分为五个步骤。
        步骤一：将源点放入到队列中。
        步骤二：将队列的头顶点u放入到已完成列表。
        步骤三：将u的所有未处理过的关联顶点放入到队列中，并标记为已处理。

        步骤四：将u顶点设置为完成顶点。
        步骤五：重复步骤二至四。

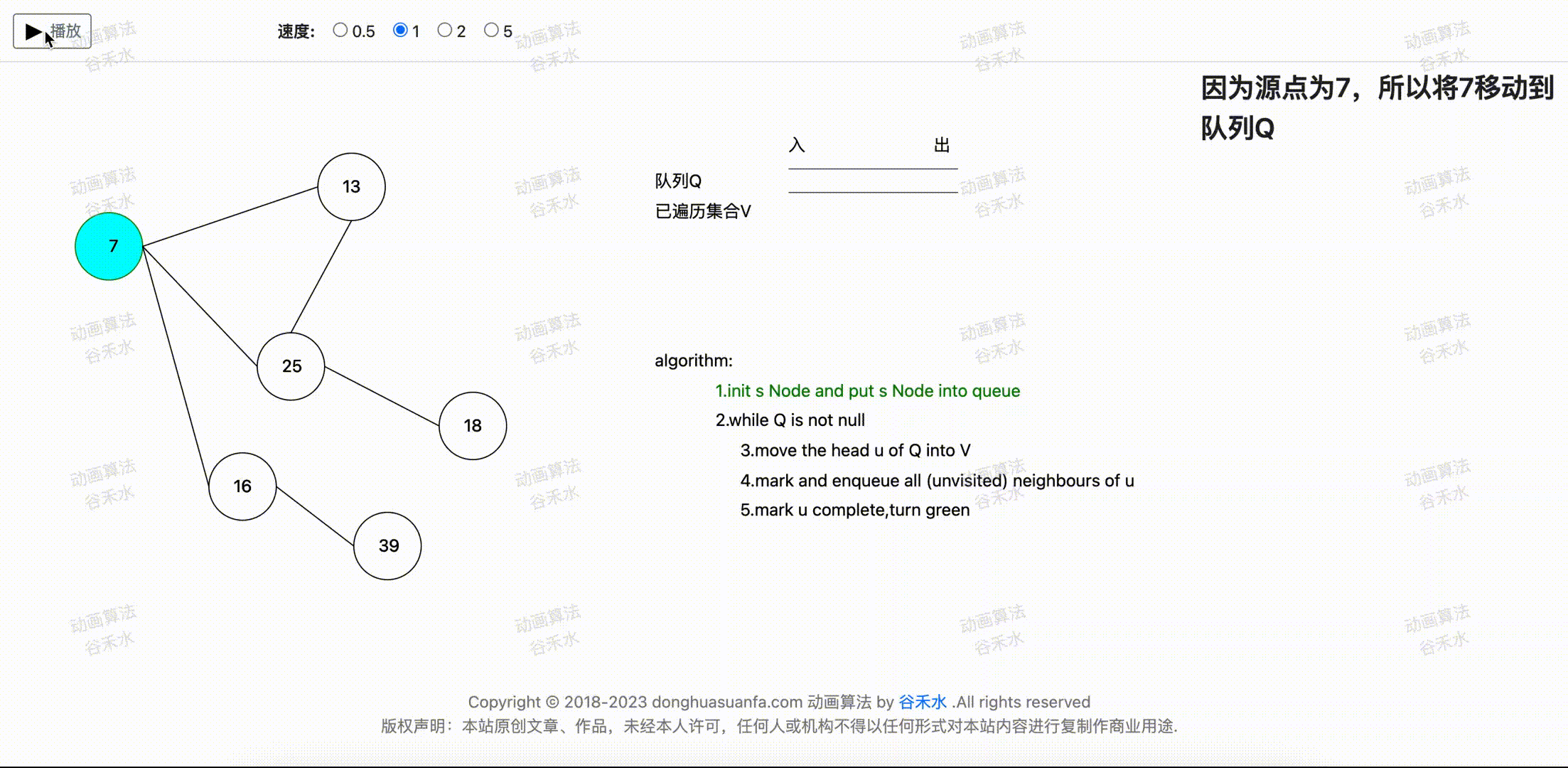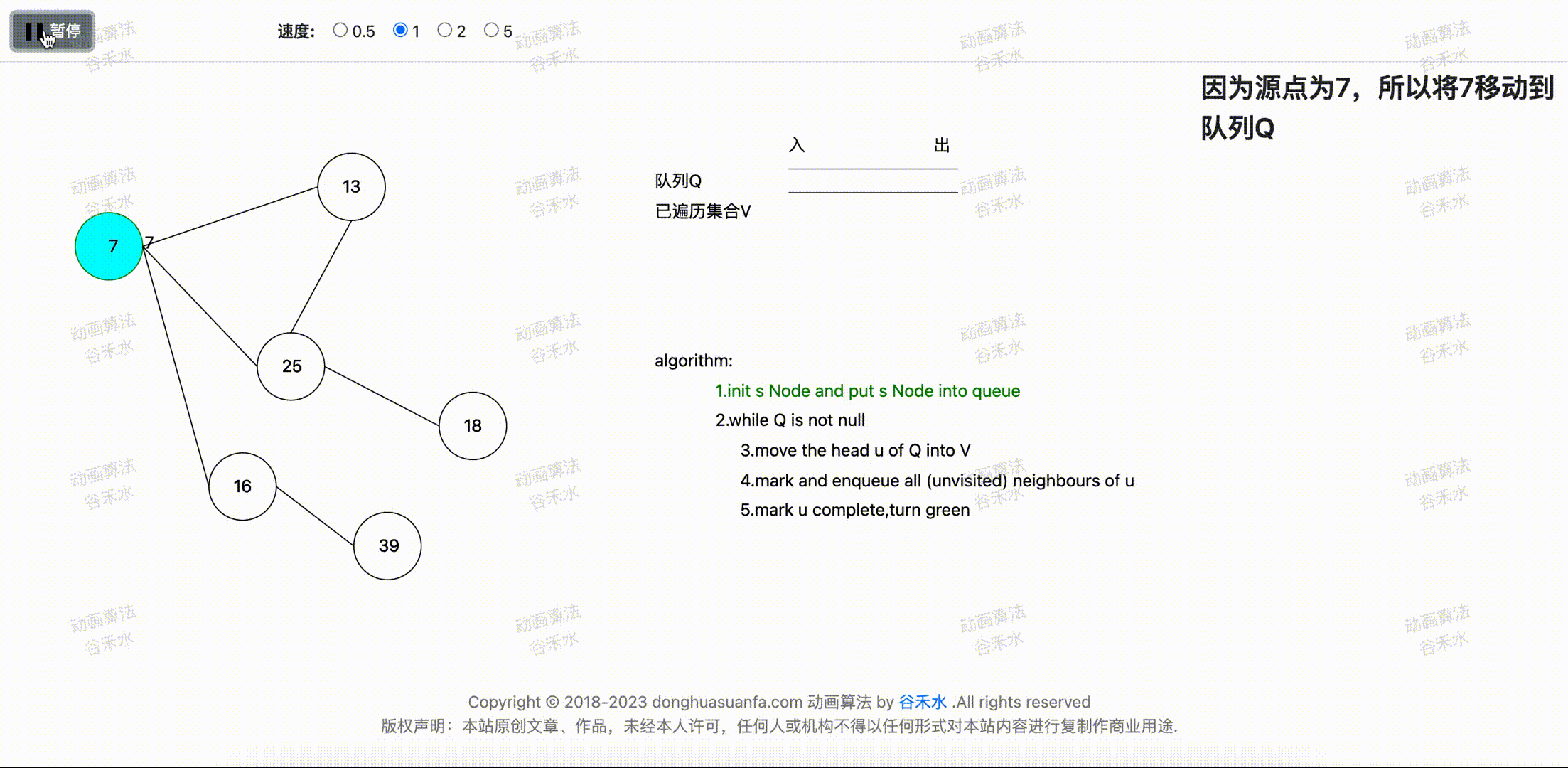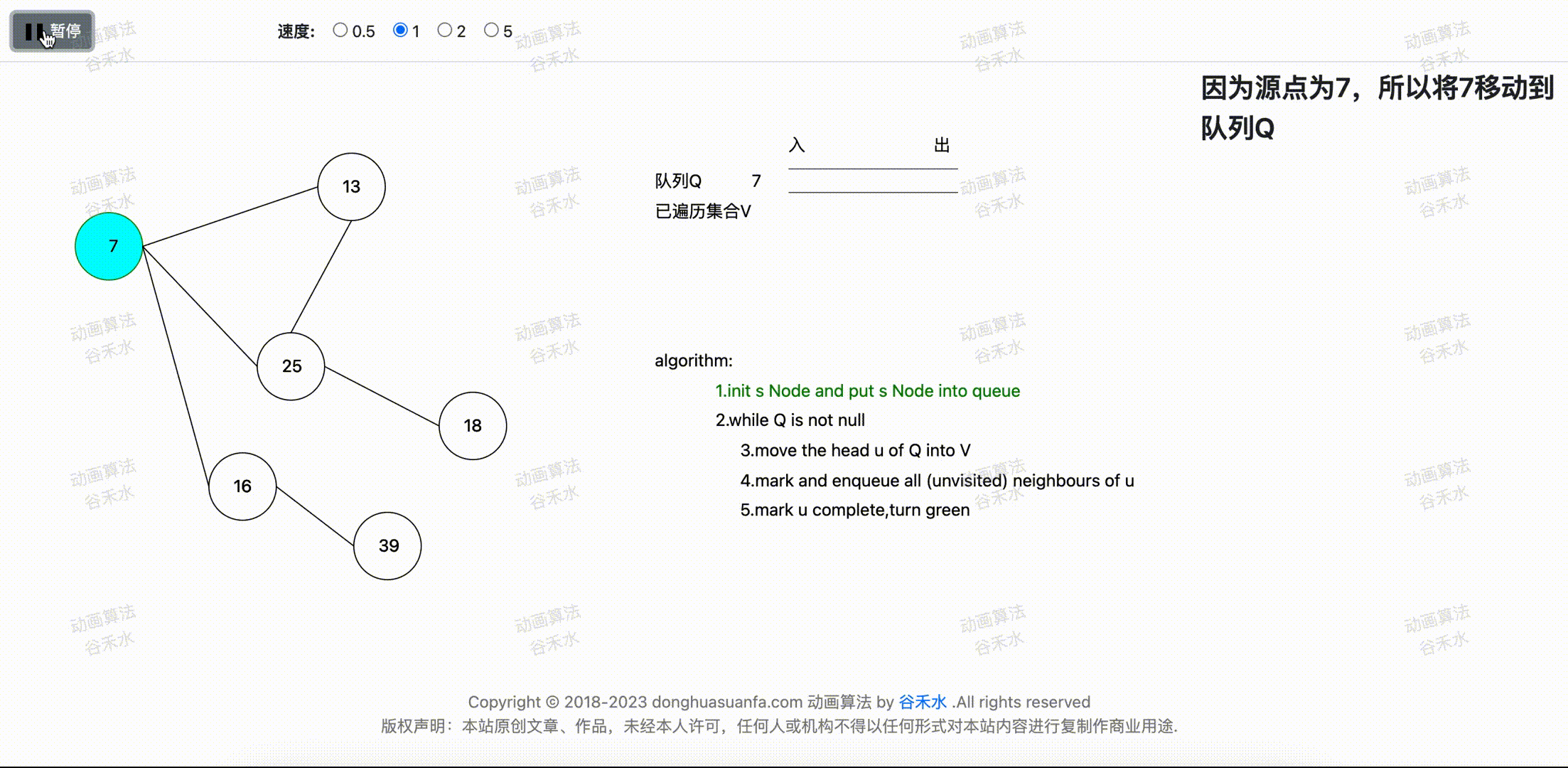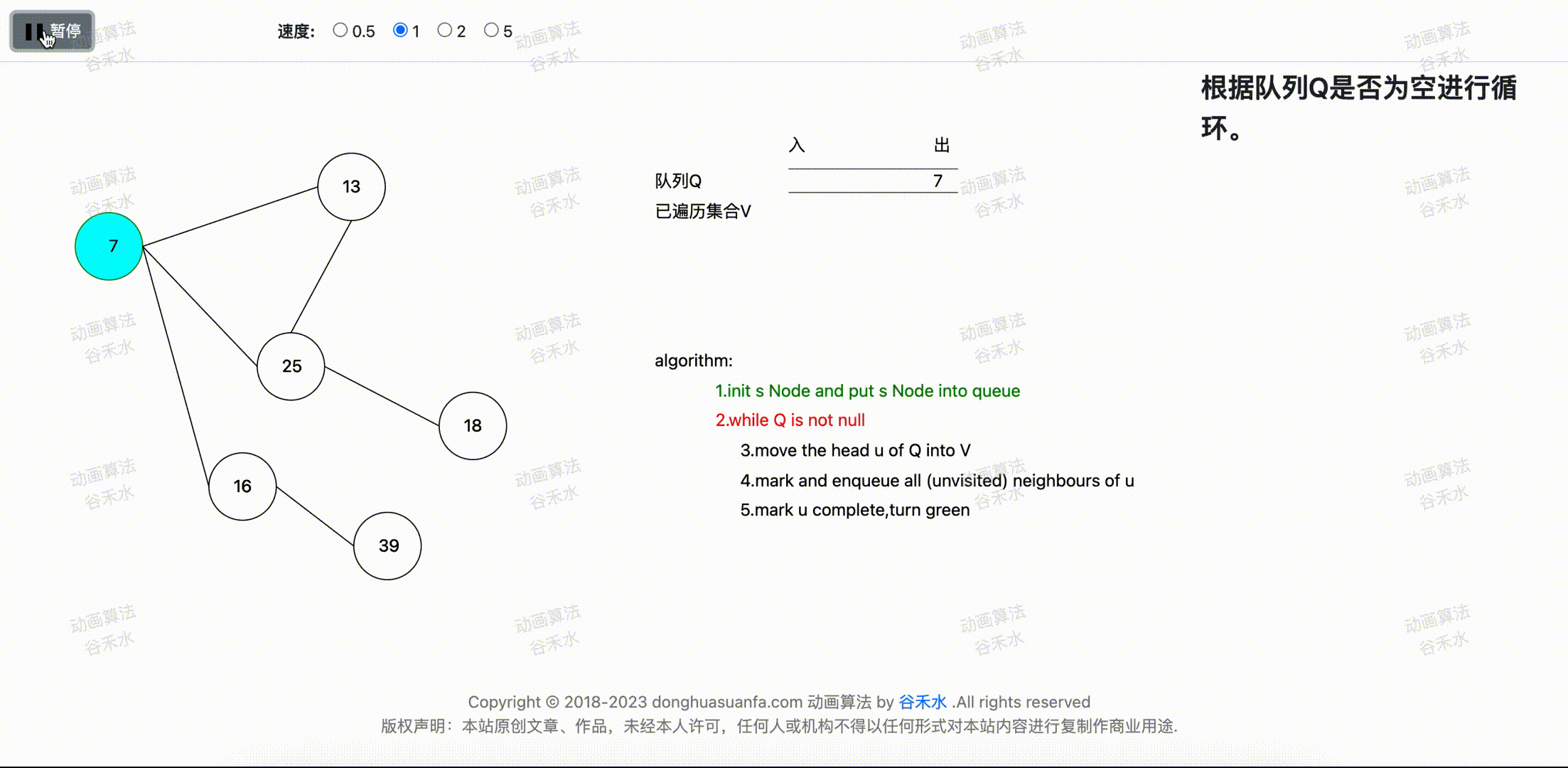
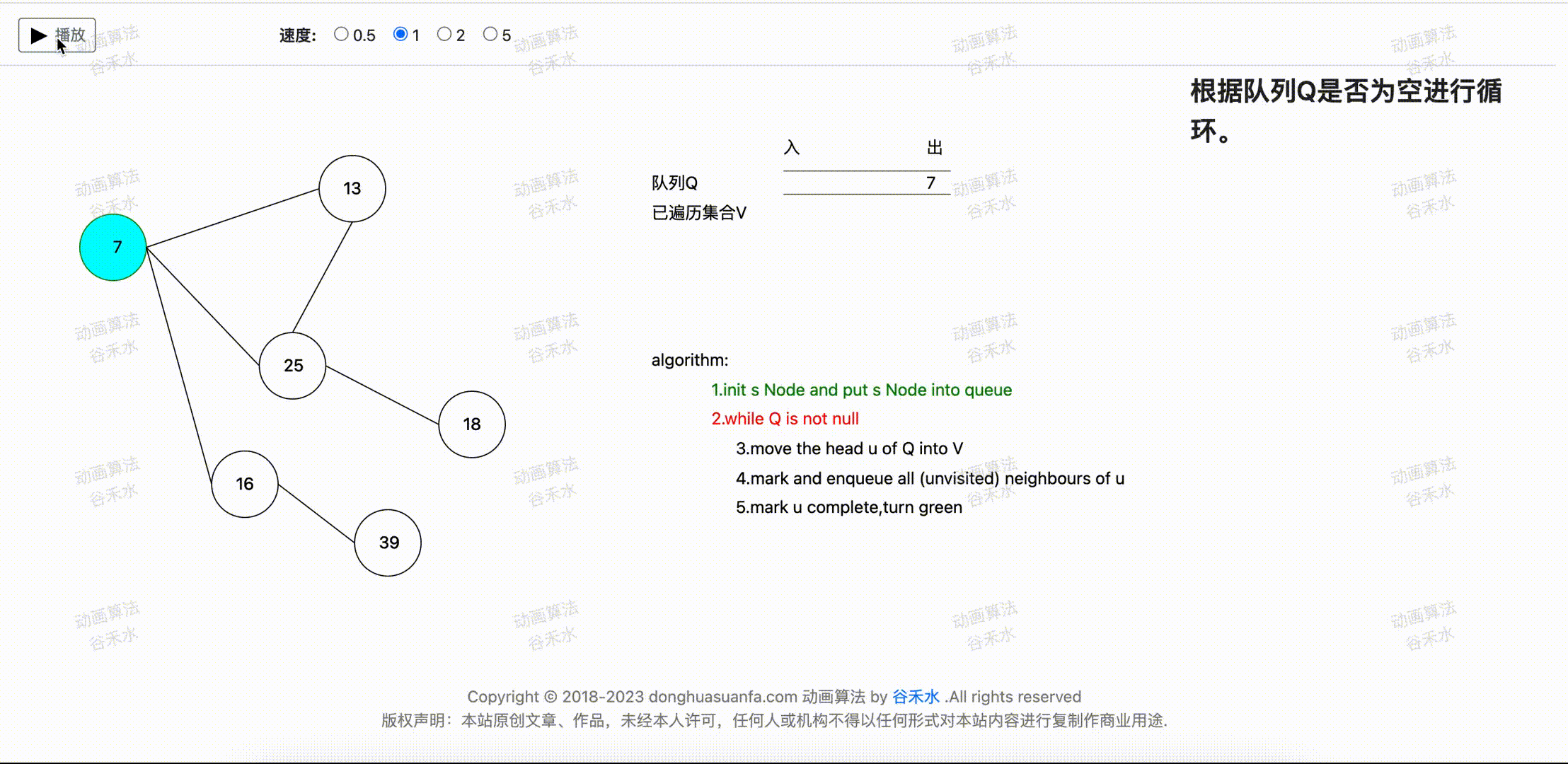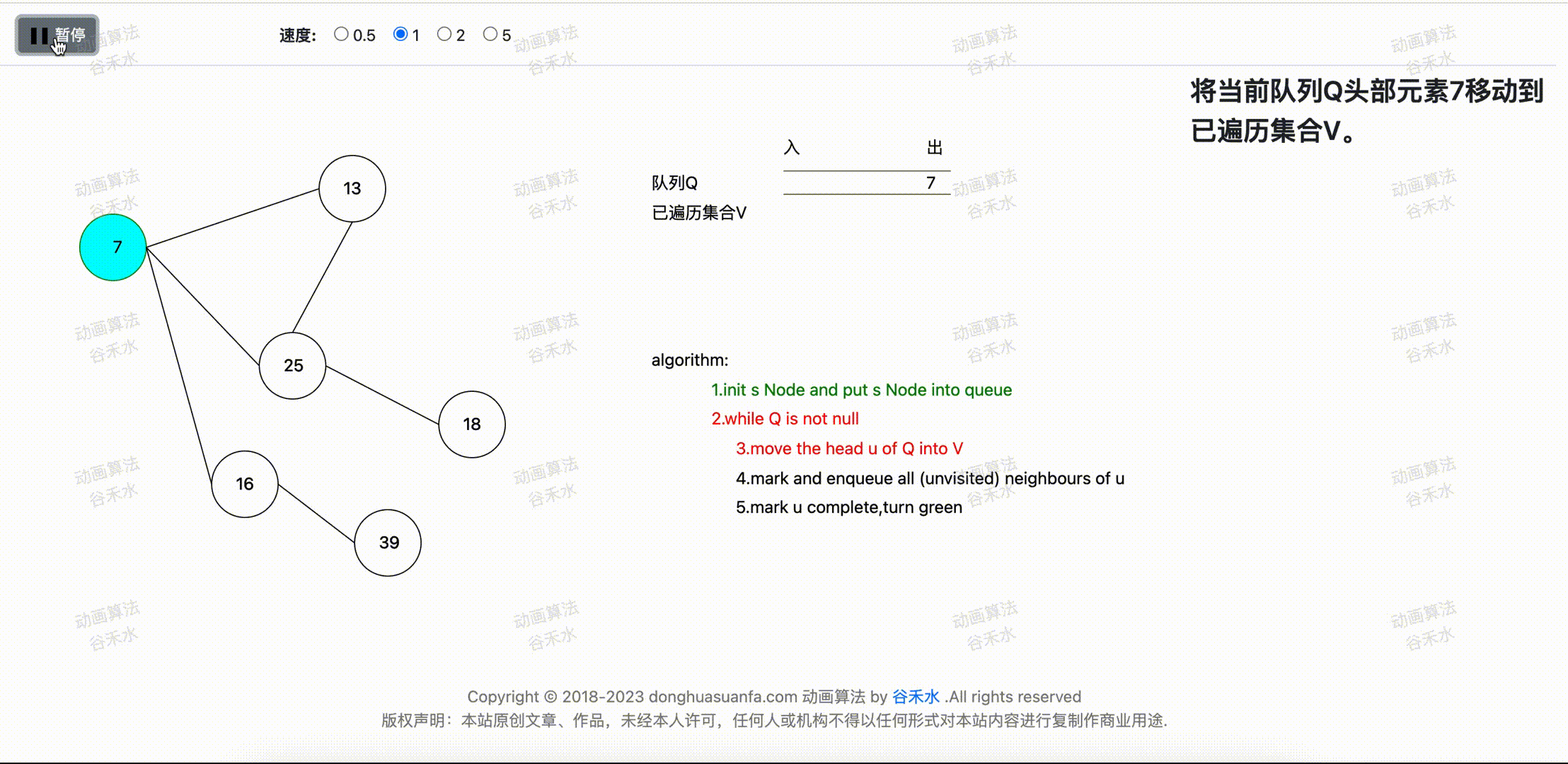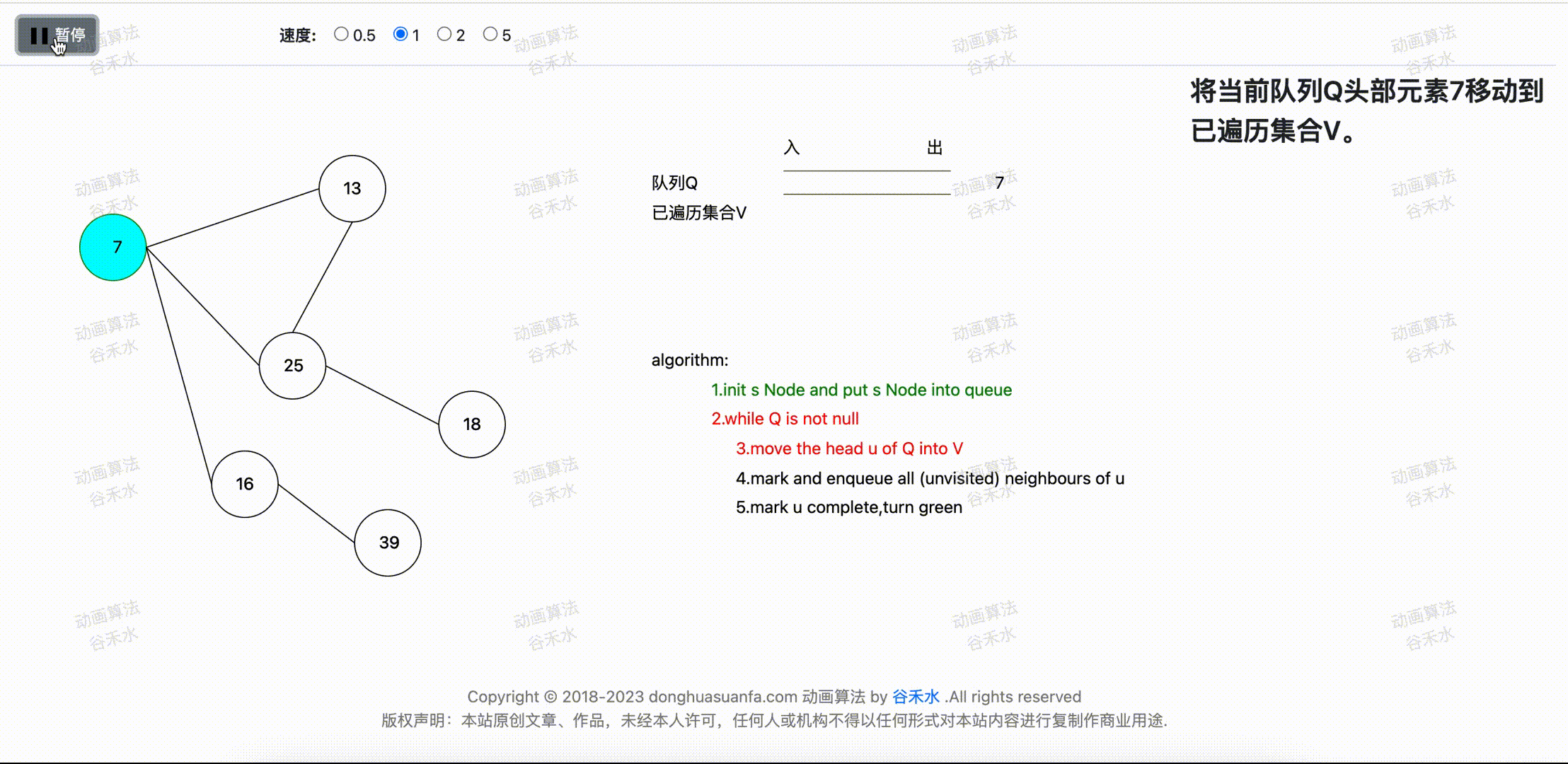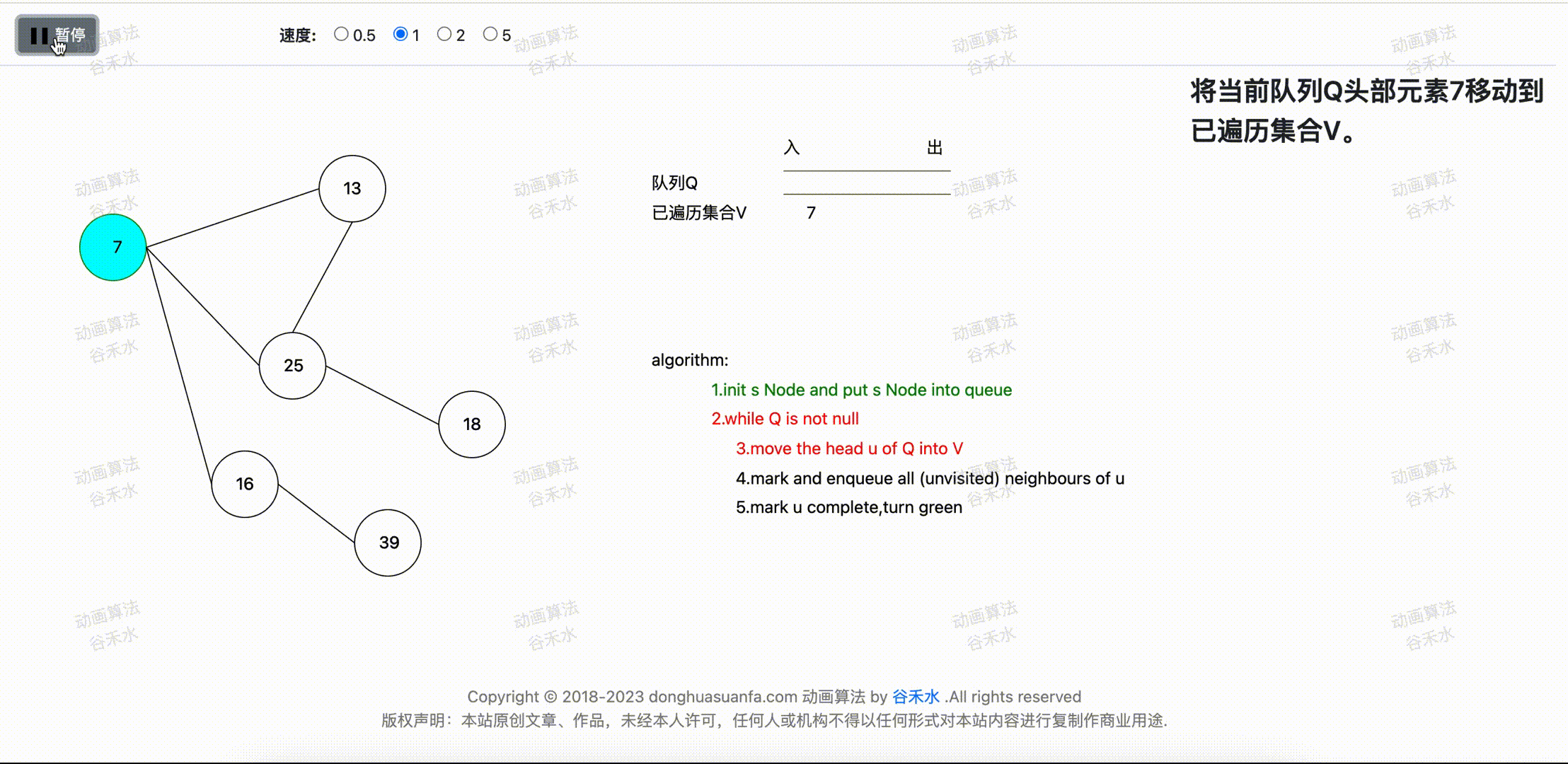
以下图为例，图的原点为7，则算法遍历图节点的顺序为7,13,25,16,18,39。

步骤一：初始化原点到队列

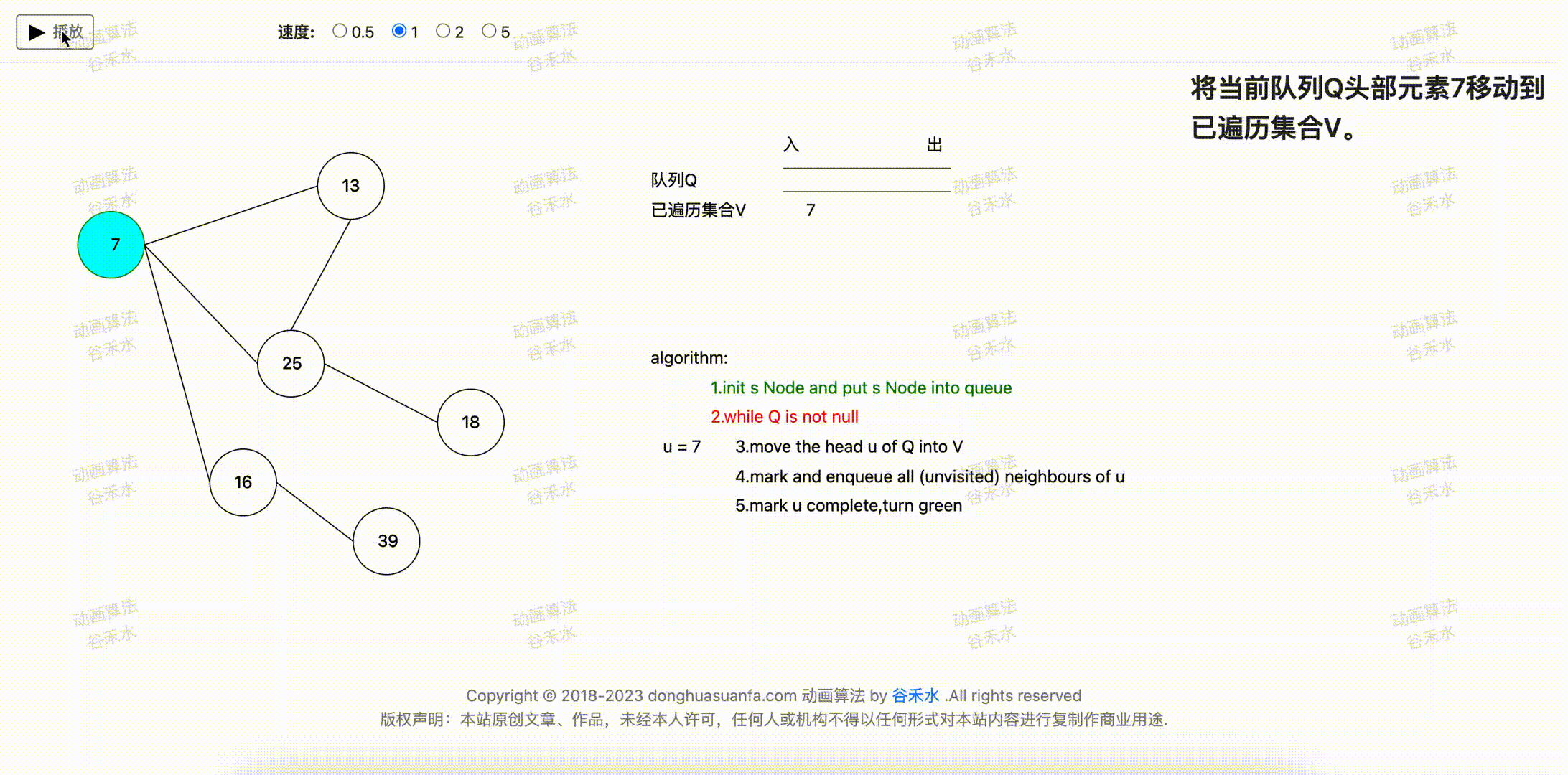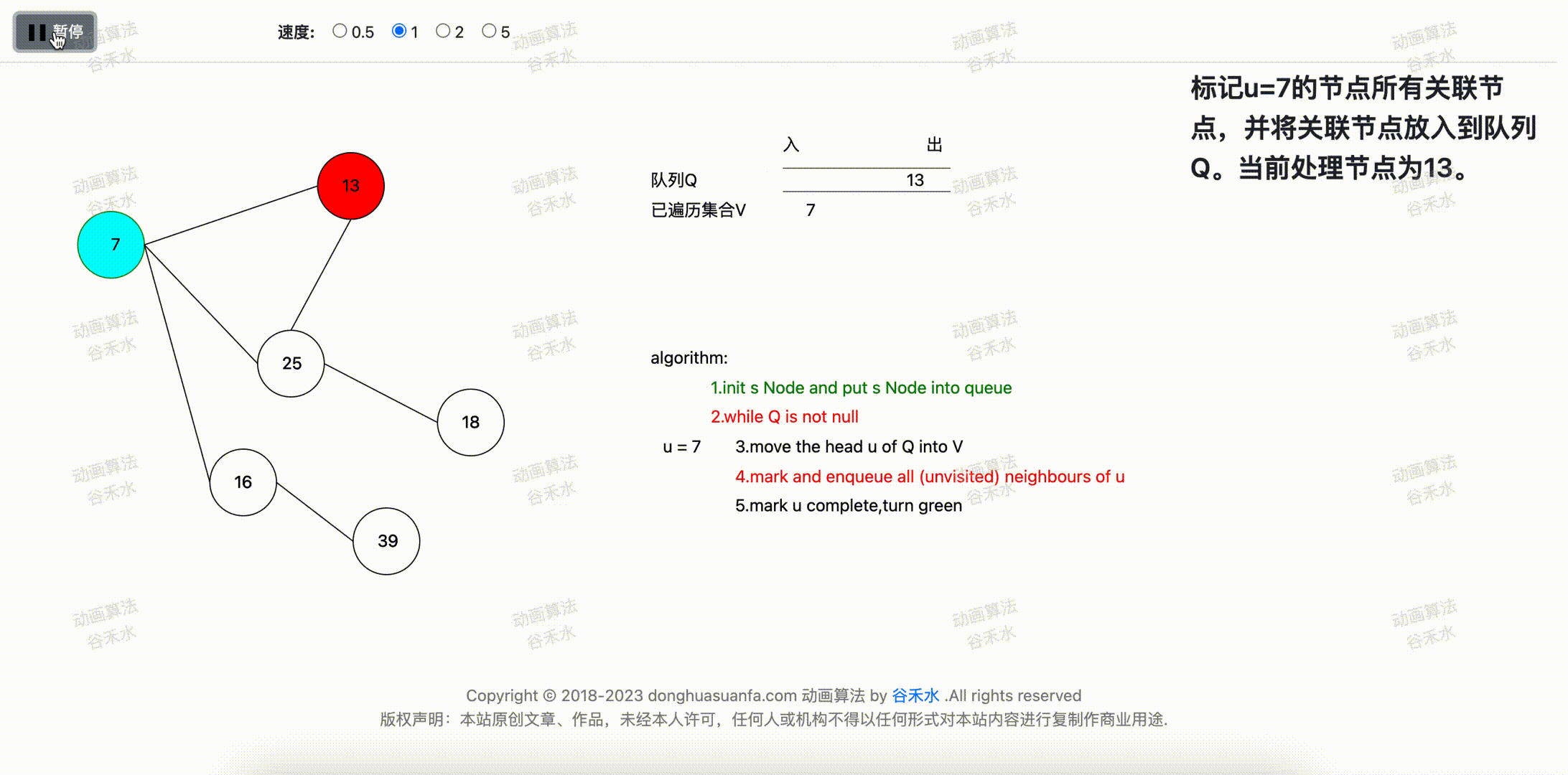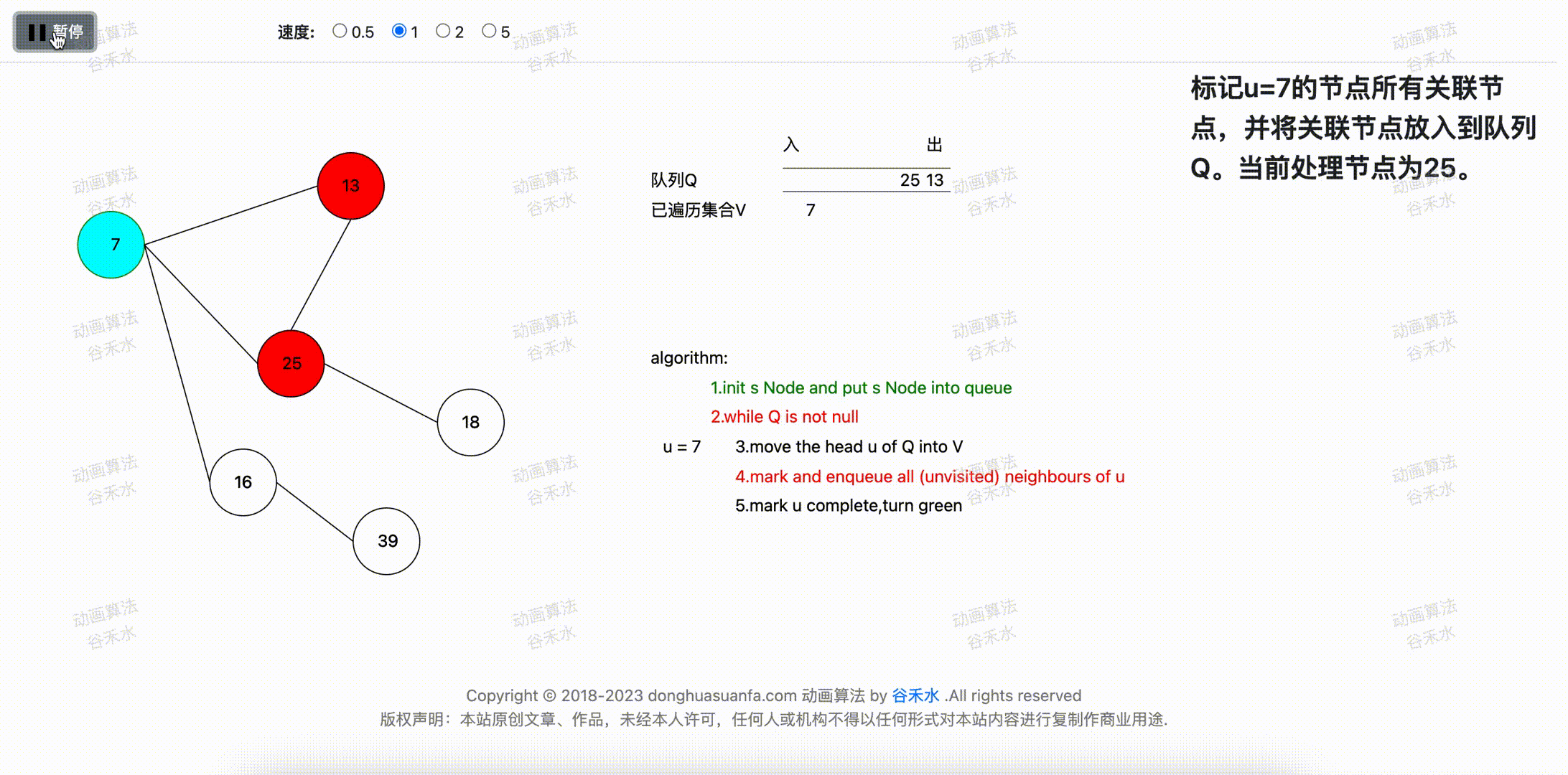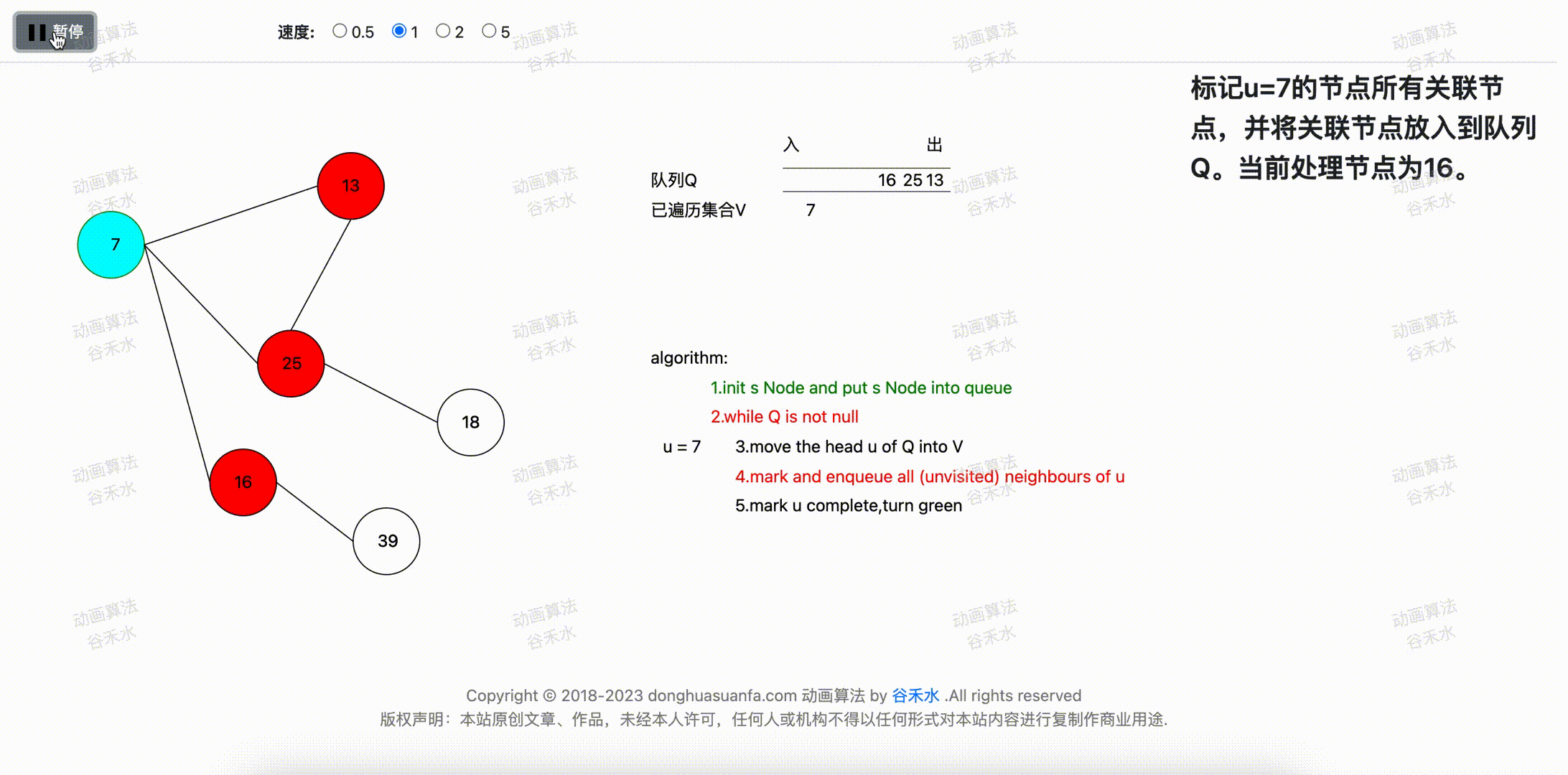
步骤演示过程如下图1-1所示。节点7为源点。算法首先将节点7移动到队列Q中。

步骤二：将队列的头顶点放入到已完成集合

将队列的头元素u放入到已遍历完成列表。当前队列的头部顶点为7，所以将7顶点移动到已遍历集合。步骤演示过程如下图2-1所示。

步骤三：将订单的关联顶点放入到队列中

将u的所有未处理过的关联顶点放入到队列中，并标记为已处理，节点颜色变为红色。
当前u的所有未处理的元素分别为13，25，16。所以将7的关联顶点分别放入队列。
步骤演示过程如下图3-1所示。

步骤四：将u顶点设置为完成节点。

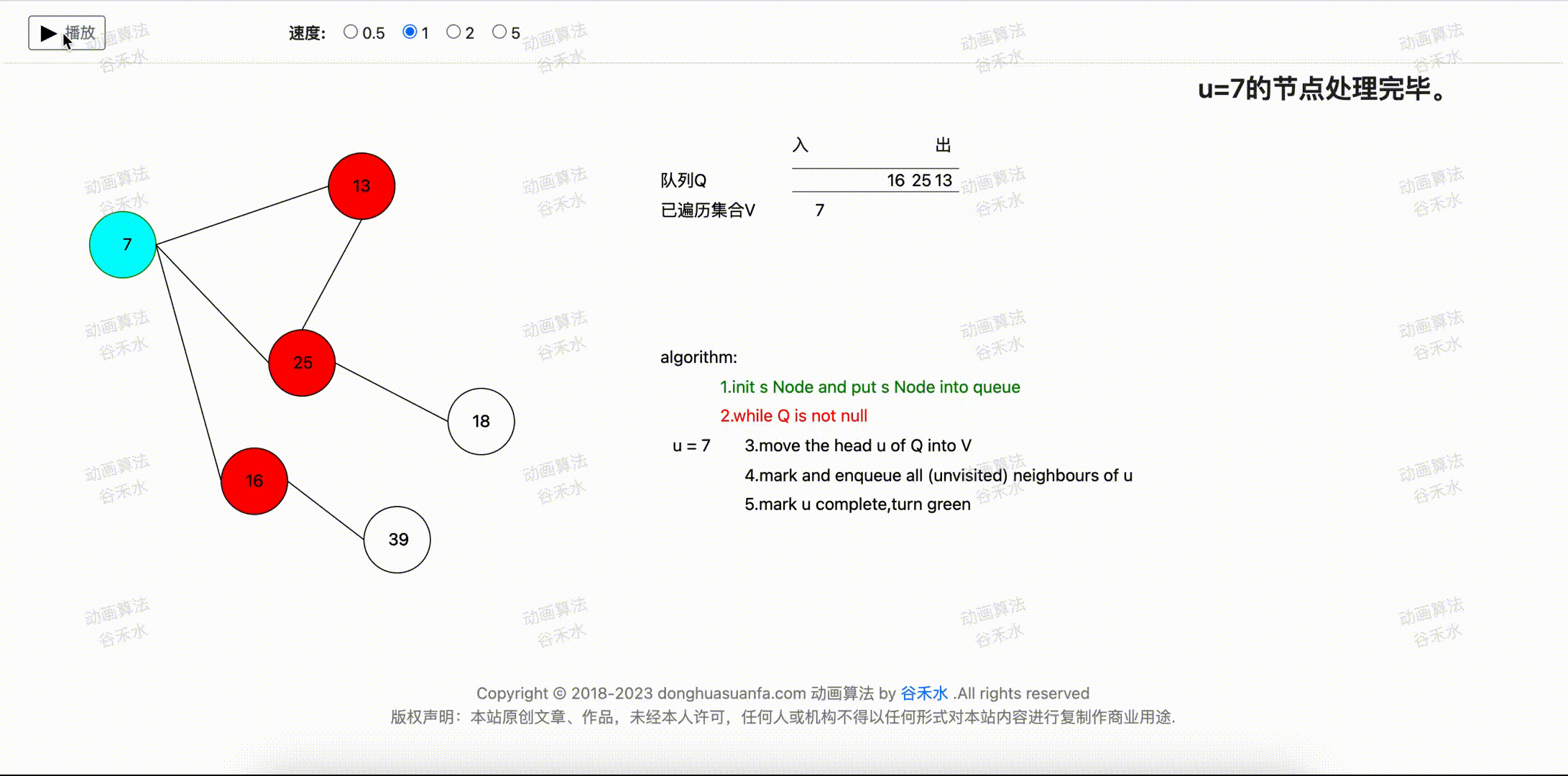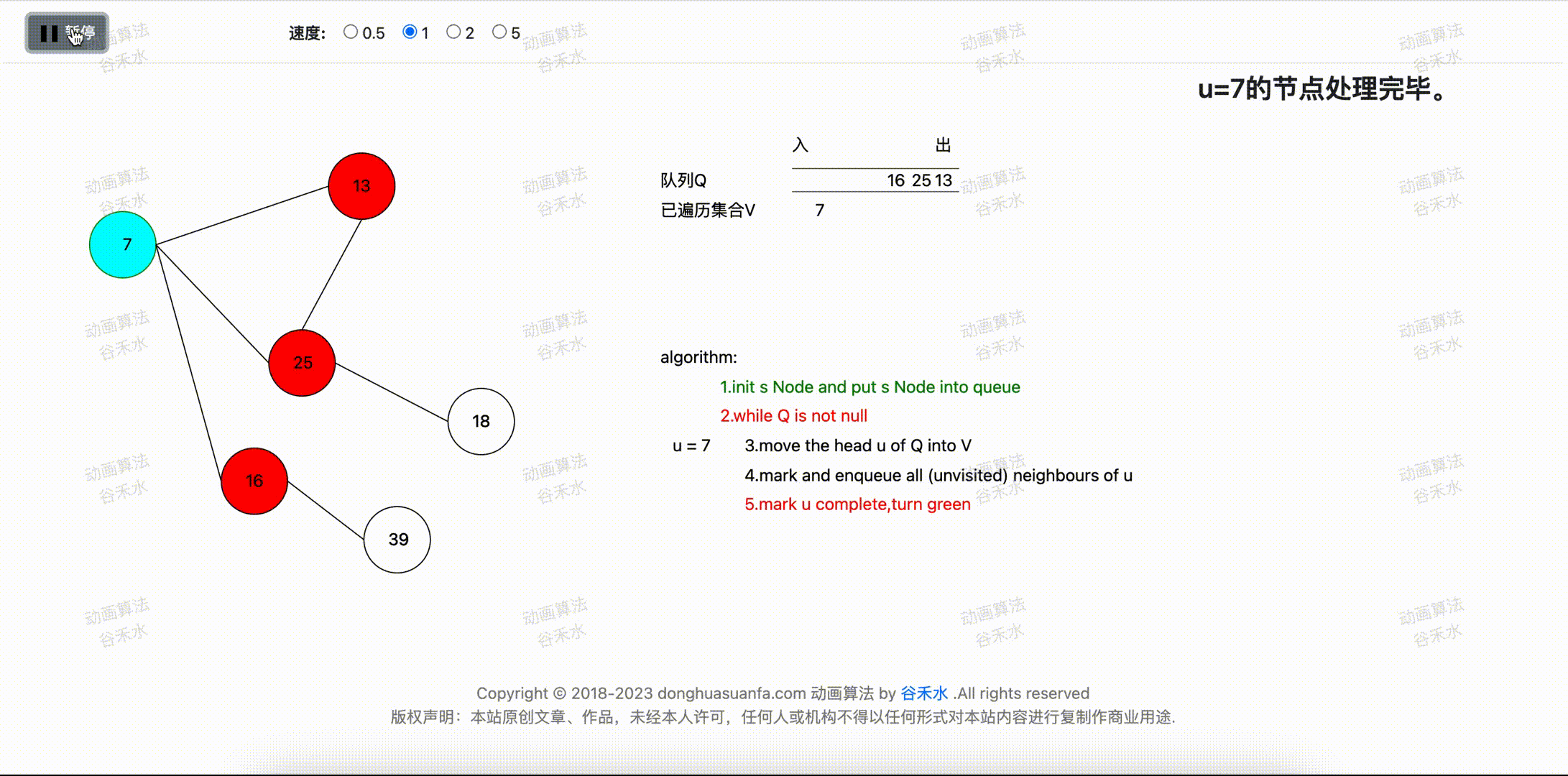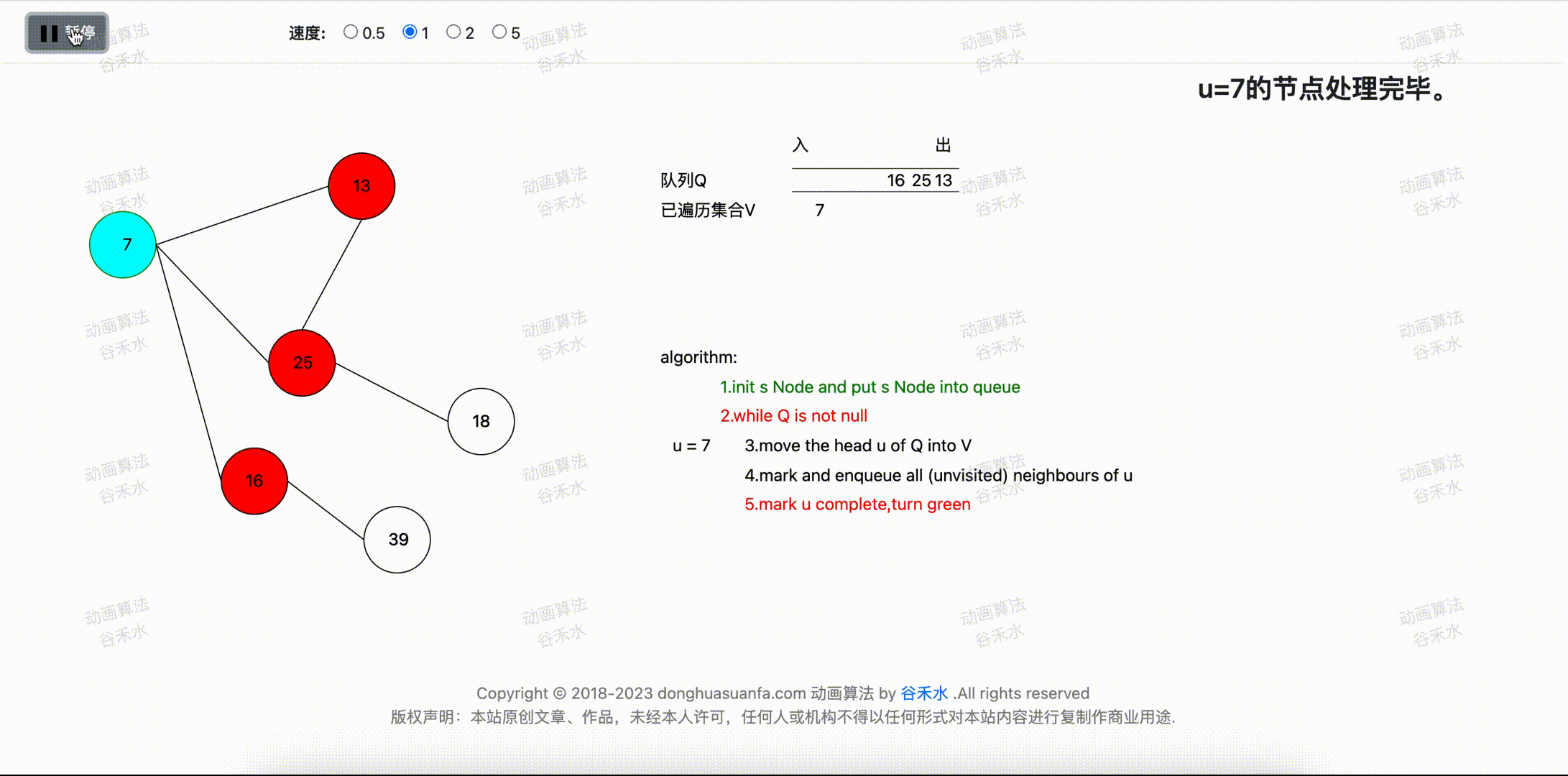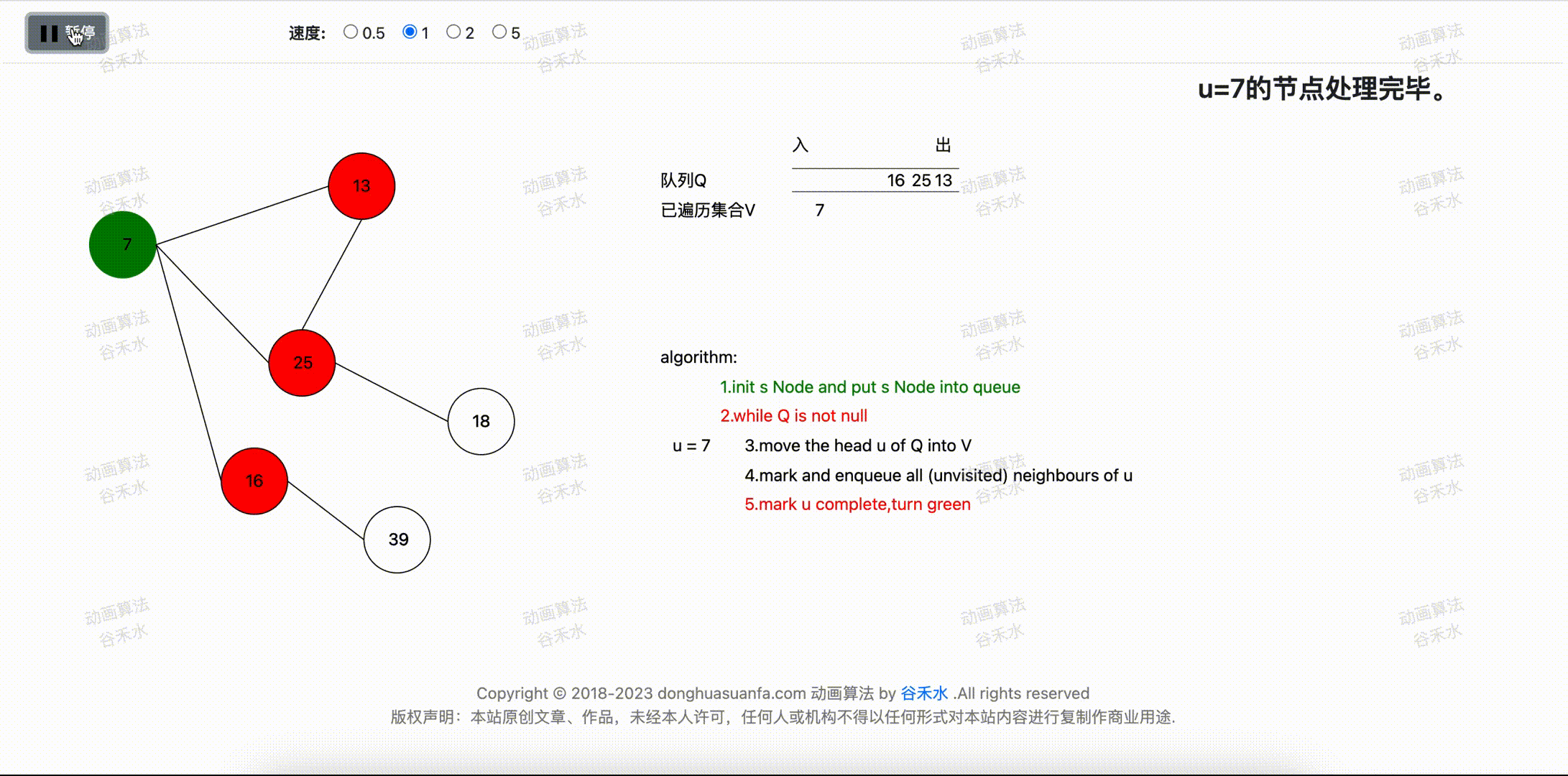
当前顶点为u=7。 将u=7顶点设置为已完成，并标记为绿色。步骤演示过程如下图3-1所示。

步骤五：重复步骤二至四。

步骤二：将队列的头部顶点13放入到已遍历结合。
步骤三：将13节点的关联元素放入到到队列， 因为13的关联顶点分别为7和25，且7已处理、25已放入队列，所以13顶点的此步骤无需处理。
步骤四：将13节点设置为完成节点。
整体步骤如图5-1所示。

        剩下的节点处理和上述步骤一致，不再赘述。

时间复杂度&空间复杂度

时间复杂度

邻接表为例：
        在BFS中，每个顶点和边只访问一次。因此，BFS的时间复杂度可以表示为O（V+E），其中V是图中顶点的数量，E是图中边的数量。

        让我们分解一下时间复杂性分析：
        1.访问所有顶点：BFS需要访问图中的所有顶点。这需要O（V）时间。
        2.检查所有边：BFS还需要检查所有边，以确定是否有任何未访问的顶点连接到当前顶点。对于每个顶点，我们需要检查其所有相邻顶点。在最坏的情况下，每个顶点与其他每个顶点都有一条边，即一个完整的图。这需要O（E）时间。

因此，BFS的总体时间复杂度为O（V+E）。

空间复杂度

        BFS的空间复杂度由队列数据结构决定，队列数据结构用于跟踪访问的顶点和要探索的顶点。在最坏的情况下，当访问所有顶点时，队列可以将所有顶点存储在图的一个级别上。因此，BFS的空间复杂度也是O（V）。

今天的文章广度优先搜索原理_深度优先算法时间复杂度分享到此就结束了，感谢您的阅读。