一、概述
CNN是卷积神经网络,通过使用一个卷积核在图像上滑动,与图像的各个部分做卷积运算,从而自动提取图像中的特征,包括边缘、纹理、形状和更高级的语义特征。通过卷积层、池化层,最后能够将输入的尺寸很大的图像,转为一个较小的特征图。
在CNN之后是MLP模型,它通过获取CNN输出的特征图,对图像进行分类。先通过一个展平层,把特征图展平成一个特征向量,从而输入后续的多层感知机,经过网络分类后得到输出。
训练CNN+MLP的过程,就是通过反向传播算法,使用交叉熵作为损失函数,用来衡量训练输出值与实际值的差别,再通过反向传播,调整MLP前向的层中的权重和偏置,同样,一直传播到卷积运算中卷积核的取值,通过训练优化,达到较好的分类效果。
由于CNN对输入尺寸较大的图像可以提取特征,而SVM作为一种使用很广泛的分类器,那么可以把CNN的特征提取和SVM分类结合起来,从而构成一种端到端的模型。
CNN+SVM结构
但是又考虑到SVM的SMO算法是一种离散优化算法,不好反向传播,所以先对CNN+MLP模型进行预训练,然后将训练好的CNN模型单独拿出来,通过CNN提取图像特征,把得到的特征向量作为SVM的输入,通过SVM对图像进行分类。
CNN+SVM流程
二、实验过程
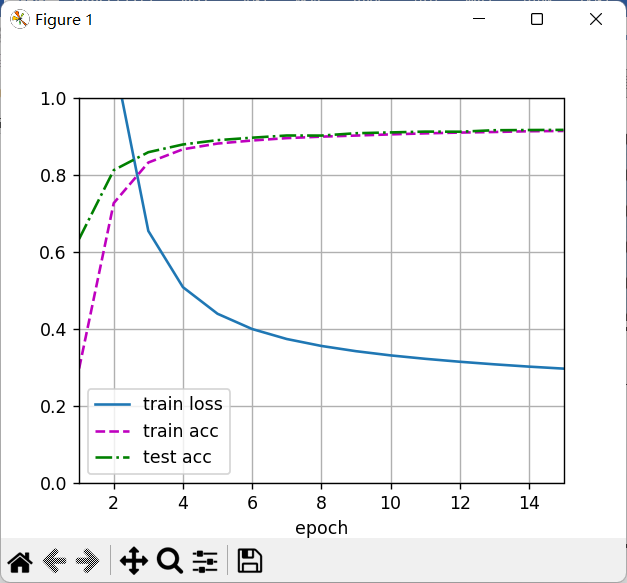
1、简单的MLP分类
这里import的包里的自定义函数都是李沐老师的动手深度学习里给的,可以直接从那里找到对应的函数。《动手学深度学习》 — 动手学深度学习 2.0.0 documentation
import zero_mlp as zm
import torch
from torch import nn
import sys
sys.path.append(r"D:\\Machining_Learning_Code\\linear_model")
import zero_softmax as zs
import matplotlib.pyplot as plt
batch_size=256
train_iter,test_iter=zm.load_data_mnist(batch_size)
net=nn.Sequential(nn.Flatten(),
nn.Linear(784,200),nn.Sigmoid(),
nn.Linear(200,10))
# print(net)
# n=input()
#net=net.to(device="cuda")
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)
lr=0.1
num_epochs=15
trainer=torch.optim.SGD(net.parameters(),lr)
loss=nn.CrossEntropyLoss(reduction='none')
zs.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
#print(net.state_dict())
#打印网络的权重和偏置,也就是网络中各层的参数
plt.show()
'''
#d2l中用到的函数,这样就不用import zs了
#就是一个累加器,存着和,调用add函数,往里加数,方便后面读取
class Accumulator:
"""在n个变量上累加"""
def __init__(self, n):
self.data = [0.0] * n
def add(self, *args):
self.data = [a + float(b) for a, b in zip(self.data, args)]
def reset(self):
self.data = [0.0] * len(self.data)
def __getitem__(self, idx):
return self.data[idx]
#计算预测正确的数量
def accuracy(y_hat,y):
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat=torch.argmax(y_hat,axis=1)
cmp = y_hat.type(y.dtype) == y
return float(cmp.type(y.dtype).sum())
#计算在指定数据集上模型的计算精度
#一个epoch的训练
def train_epoch_ch3(net, train_iter, loss, updater): #@save
"""训练模型一个迭代周期(定义见第3章)"""
# 将模型设置为训练模式
if isinstance(net, torch.nn.Module):
net.train()
# 训练损失总和、训练准确度总和、样本数
metric = Accumulator(3)
for X, y in train_iter:
# 计算梯度并更新参数
y_hat = net(X)
l = loss(y_hat, y)
if isinstance(updater, torch.optim.Optimizer):
# 使用PyTorch内置的优化器和损失函数
updater.zero_grad()
l.mean().backward()
updater.step()
else:
# 使用定制的优化器和损失函数
l.sum().backward()
updater(X.shape[0])
metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
# 返回训练损失和训练精度
return metric[0] / metric[2], metric[1] / metric[2]
'''
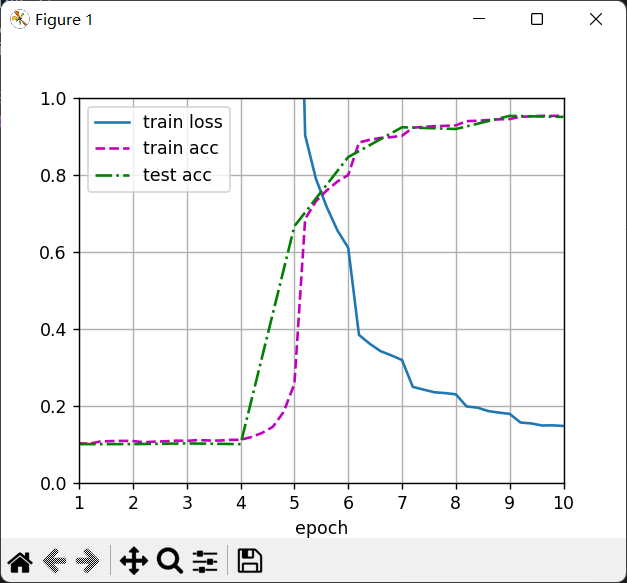
2、CNN+MLP分类
预训练CNN+MLP,两个卷积层,卷积核大小为5*5,填充数目为2,卷积输出再通过sigmoid层,接着使用平均池化,池化大小为2,滑动步长为2,接着送入展平层,再通过三层线性层,400*120,120*84,84*10
import torch
from torch import nn
import sys
sys.path.append(r"D:\\Machining_Learning_Code\\linear_model")
import zero_softmax as zs
#这里用到的包都在上一个程序末尾给了,计算准确率和累加器定义
import softmax_hand_writing as shw
import d2l
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.svm import SVC
import torch.nn.functional as F
import numpy as np
import time
net=nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10)
)
batch_size = 256
train_iter, test_iter = shw.load_data_mnist(batch_size=batch_size)
def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
"""使用GPU计算模型在数据集上的精度"""
if isinstance(net, nn.Module):
net.eval() # 设置为评估模式
if not device:
device = next(iter(net.parameters())).device
# 正确预测的数量,总预测的数量
metric = zs.Accumulator(2)
with torch.no_grad():
for X, y in data_iter:
if isinstance(X, list):
# BERT微调所需的(之后将介绍)
X = [x.to(device) for x in X]
else:
X = X.to(device)
y = y.to(device)
metric.add(zs.accuracy(net(X), y), y.numel())
return metric[0] / metric[1]
#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
"""用GPU训练模型(在第六章定义)"""
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
print('training on', device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss()
animator = zs.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
num_batches =len(train_iter)
for epoch in range(num_epochs):
# 训练损失之和,训练准确率之和,样本数
metric = zs.Accumulator(3)
net.train()
for i, (X, y) in enumerate(train_iter):
optimizer.zero_grad()
X, y = X.to(device), y.to(device)
y_hat = net(X)
l=loss(y_hat,y)
#l = loss2(net[i].weight, y_hat, y, C)
l.backward()
optimizer.step()
with torch.no_grad():
metric.add(l * X.shape[0], zs.accuracy(y_hat, y), X.shape[0])
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch + 1, (None, None, test_acc))
# for name,params in net.named_parameters():
# print(name[-1])
# print(params[-1])
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
f'test acc {test_acc:.3f}')
print(f'on {str(device)}')
num_epochs=10
def test():
lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, device='cuda')
plt.show()
# test()
print("CNN训练!\n")
start =time.time()
test()
end = time.time()
print("训练CNN花费的时间:",int(end-start),"秒")3、CNN+SVM
这里是先用CNN预训练的LeNet,然后再把原始数据送入CNN提取特征,之后得到的特征向量作为SVM的输入数据,通过训练SVM得到最后的分离超平面,并在测试集上验证准确率和召回率。
import torch
from torch import nn
import sys
sys.path.append(r"D:\\Machining_Learning_Code\\linear_model")
import zero_softmax as zs
import softmax_hand_writing as shw
import d2l
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.svm import SVC
import torch.nn.functional as F
import numpy as np
import time
class GaussionKernel(nn.Module):
def __init__(self, mark_points, sigma=0.1):
super(GaussionKernel, self).__init__()
self.sigma = sigma
self.mark_points = mark_points
def forward(self, X):
with torch.no_grad():
# realize vectorization by broadcast mechanism
z = ((X.unsqueeze(1) - self.mark_points.unsqueeze(0))**2).sum(dim=2)
return torch.exp(-z/(2*self.sigma**2))
net=nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10)
)
batch_size = 256
train_iter, test_iter = shw.load_data_mnist(batch_size=batch_size)
def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
"""使用GPU计算模型在数据集上的精度"""
if isinstance(net, nn.Module):
net.eval() # 设置为评估模式
if not device:
device = next(iter(net.parameters())).device
# 正确预测的数量,总预测的数量
metric = zs.Accumulator(2)
with torch.no_grad():
for X, y in data_iter:
if isinstance(X, list):
# BERT微调所需的(之后将介绍)
X = [x.to(device) for x in X]
else:
X = X.to(device)
y = y.to(device)
metric.add(zs.accuracy(net(X), y), y.numel())
return metric[0] / metric[1]
#@save
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
"""用GPU训练模型(在第六章定义)"""
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
print('training on', device)
net.to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss()
animator = zs.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
num_batches =len(train_iter)
for epoch in range(num_epochs):
# 训练损失之和,训练准确率之和,样本数
metric = zs.Accumulator(3)
net.train()
for i, (X, y) in enumerate(train_iter):
optimizer.zero_grad()
X, y = X.to(device), y.to(device)
y_hat = net(X)
l=loss(y_hat,y)
#l = loss2(net[i].weight, y_hat, y, C)
l.backward()
optimizer.step()
with torch.no_grad():
metric.add(l * X.shape[0], zs.accuracy(y_hat, y), X.shape[0])
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch + 1, (None, None, test_acc))
# for name,params in net.named_parameters():
# print(name[-1])
# print(params[-1])
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
f'test acc {test_acc:.3f}')
print(f'on {str(device)}')
num_epochs=10
def test():
lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, device='cuda')
plt.show()
# test()
print("CNN训练!\n")
start =time.time()
test()
end = time.time()
print("训练CNN花费的时间:",int(end-start),"秒")
#****************************************************************************************************
#上面是CNN+MLP
#下面是CNN+SVM
#****************************************************************************************************
train_iter, test_iter = shw.load_data_mnist(batch_size=256)
num_batches =len(train_iter)
device='cuda'
net.to(device)
# print("看看net的参数\n")
# for name,params in net.named_parameters():
# print(name[-1])
# print(params[-1])
print("SVM的训练开始了!")
for epoch in range(1):
# 训练损失之和,训练准确率之和,样本数
correct_pre=0
list_test=[]
list_test_targets=[]
list_train=[]
list_targets=[]
for i, (input, target) in enumerate(train_iter):
input, target= input.to(device), target.to(device)
#无法直接访问某一层的输出,所以用层的forward,前向传播
for i in range(len(net)):
input = net[i](input)
if i == 6:
y_hat = net[i](input)
target=target.cpu().detach().numpy()
y_hat=y_hat.cpu().detach().numpy()
list_train.append(y_hat)
list_targets.append(target)
#测试集数据生成,先通过net,获取展平层的输出特征向量,作为SVM的输入特征向量
for i, (input, target) in enumerate(test_iter):
input, target= input.to(device), target.to(device)
#无法直接访问某一层的输出,所以用层的forward,前向传播
for i in range(len(net)):
input = net[i](input)
if i == 6:
y_hat = net[i](input)
target=target.cpu().detach().numpy()
y_hat=y_hat.cpu().detach().numpy()
list_test.append(y_hat)
list_test_targets.append(target)
# print(list_train[0].shape)
# print(len(list_targets))
# print(list_targets[0].shape)
# print(len(list_train))
list_train_all=[]
list_targets_all=[]
list_test_all=[]
list_test_targets_all=[]
for i in range (235):
for j in range(len(list_targets[i])):
list_train_all.append(list_train[i][j])
list_targets_all.append(list_targets[i][j])
for i in range(len(list_test)):
for j in range(len(list_test[i])):
list_test_all.append(list_test[i][j])
list_test_targets_all.append(list_test_targets[i][j])
# list_inputs.reshape(())
print("开始训练SVM\n")
start =time.time()
clf = SVC(C=3.0,max_iter=-1,decision_function_shape="ovr")
clf.fit(list_train_all , list_targets_all)
end = time.time()
print("训练SVM花费的时间:",int(end-start),"秒\n")
start =time.time()
train_result = clf.predict(list_train_all)
end = time.time()
print("train_set测试结果花费的时间:",int(end-start),"秒\n")
correct_pre=int(sum(train_result==list_targets_all))
print("在train_set上的正确率为:",float(correct_pre/len(list_targets_all)),"\n")
start =time.time()
test_result=clf.predict(list_test_all)
end = time.time()
print("test_set测试结果花费的时间:",int(end-start),"秒\n")
test_correct_pre=int(sum(test_result==list_test_targets_all))
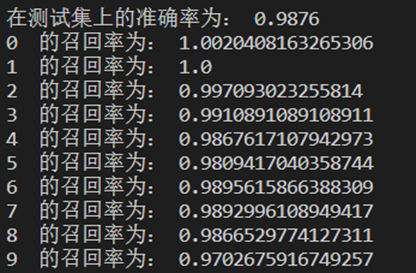
print("在测试集上的准确率为:",float(test_correct_pre/len(list_test_targets_all)))
for i in range(10):
base=[i]*len(list_test_targets_all)
base=np.array(base)
all_i=sum(list_test_targets_all==base)
pre=[]
for j in range(len(test_result)):
if test_result[j]==list_test_targets_all[j] & test_result[j]==i:
pre.append(test_result[j])
pre_i=len(pre)
recall_i=pre_i/all_i
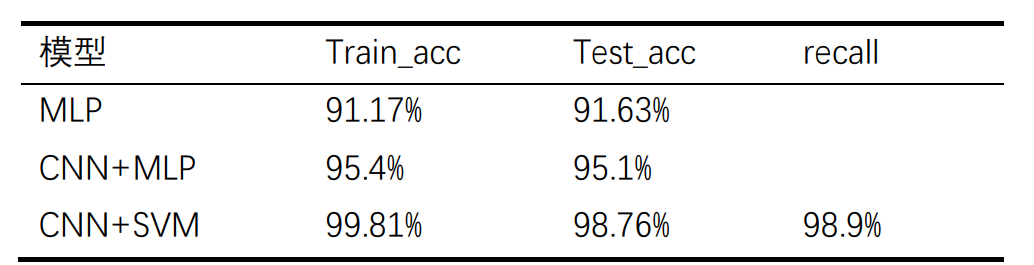
print(i," 的召回率为:",recall_i)通过CNN的输出特征向量再训练SVM,得到在训练集上准确率为99.685%,在测试集上准确率98.76%,平均10类的召回率98.9%。
三、总结
目前能想到的端到端的实现CNN+SVM就是把CNN的特征输出作为SVM的输入,因为CNN对于特征提取效果很好,也可以降低输入的信息量,SVM又可以进行线性或者非线性的多分类问题,结合二者的优势,最终表现效果也还不错,而且这种做法应该算是最普遍和简单的。也看到一种想法是将SVM应用到卷积的过程中,以提取更多的图片信息量,但是暂时还想不到如何把这两个结合起来。
今天的文章基于cnn的手写数字识别_手写数字识别数据集「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/87262.html