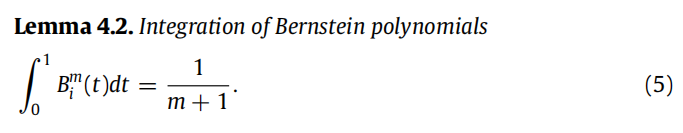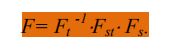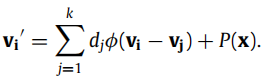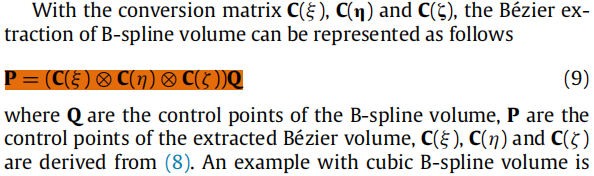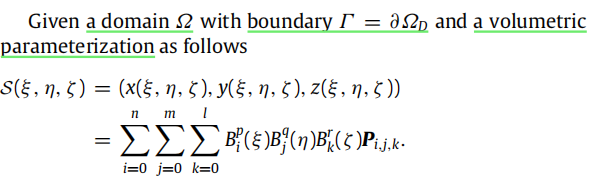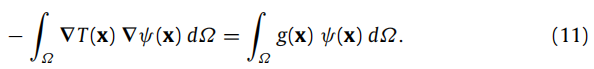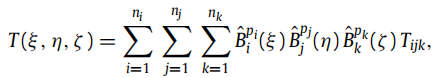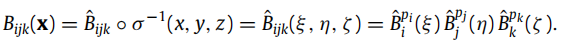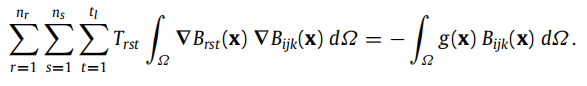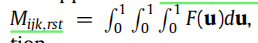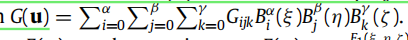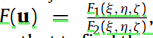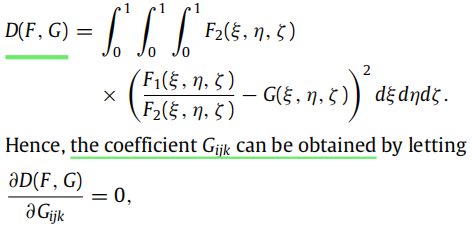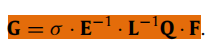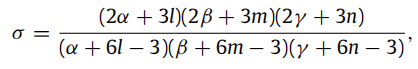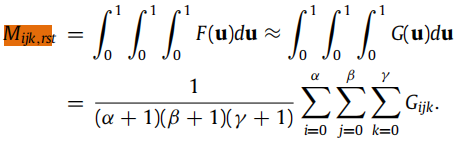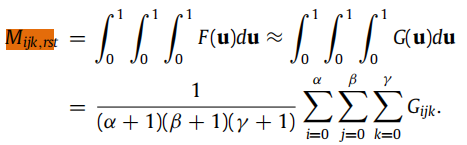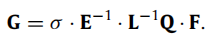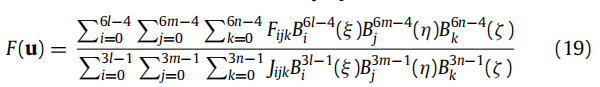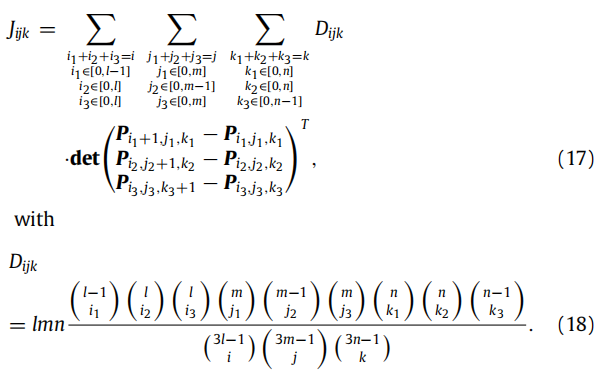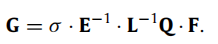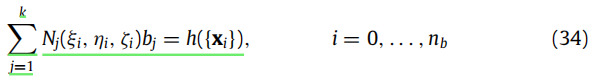拓扑一致性是什么意思_一致连续的几何意义「建议收藏」

《Isogeometric computation reuse method for complex objects with topology-consistent volumetric parameterization》
本篇论文主要讲的是在对拓扑一致体参数化的复杂模型进行等几何分析时如何重用一些计算以加快分析速度。应用场景：有一组待分析的拓扑一致的模型，或是对同一模型进行形状优化时，可以重用第一个模型的某些计算以加快后续模型的分析速度。
关键词：拓扑一致体参数化，等几何分析，计算重用
本篇论文重点内容有三部分：

1. 复杂三维模型的一致B样条体参数化（如何对一组拓扑一致的模型构造体参数化）
2. 通过bezier提取和多项式逼近的无积分等几何分析（本文提出的一种无积分的等几何分析方法）
3. 对于一致体参数化模型的计算重用（有哪些量是可以计算重用的）

注意：
等几何分析的最大特点就是：在物理仿真时所用的试函数就是模型表达式中的基函数，也就是用模型表示中的基函数的线性组合来表示仿真结果
本文重点内容的第二部分中无积分等几何分析的特点是：把第一部分得到的b样条体参数化转化成了用bernstein基函数表示的形式后再进行分析的，berstein基函数具有良好的积分性质，可以避免复杂的积分

一. Consistent B-spline volumetric parameterization of complex 3D models 复杂三维模型的一致b样条体参数化

基础知识：cross parameterization交叉参数化
关于交叉参数化，本篇论文参考的文章是《Constructing common base domain by cues from Voronoi diagram》，而这篇参考文献主要是在《Cross-Parameterization and Compatible Remeshing of 3D Models》基础上对基础域的构造进行改进。
（1）surface parameterization：计算一个曲面到一个域的映射
（2）对于亏格为0的三维模型，通常做法是把模型映射到一个球面上，但当模型比较复杂时，这种映射方式就不太理想。
因此，出现一种更灵活的框架：使复合基本域，模型曲面首先被分割成简单的复合域（一些方法中称为base domain基本域）。这样，通过把网格曲面分区参数化到相应的具有相同边界条件的基本域上来获得整个模型的全局参数化。
（3）cross-parameterization：当一组模型被一致地划分，被所有模型共享的基本域称为公共基本域（common base domain）。把这些基本域看作桥梁，可以找到这组模型之间的映射，这种映射称为一致网格参数化或是交叉参数化。

我的理解：把模型A映射到它的基本域A’，模型B映射到它的基本域B’，A’和B’之间的映射比较容易找到，然后就可以得到A和B之间的映射（交叉参数化最初是为了得到双射参数化而出现的方法）
本文对一组模型找出公共基本域，所有模型都以这个公共基本域为模板进行一致地划分，从而保证所有模型的划分一致。一致划分后，每个划分的区域都可相应地映射到一个基本域上，一个基本域用一个b样条体表示，对于同一个基本域，阶数应该是相同的，不同模型的控制点位置不同，那么就有很多计算是可以共用的。本文应用交叉参数化的方法主要是为了保证拓扑一致的一组模型的划分一致，基本域可以共用一些变量，从而实现计算重用。

径向基函数Radial basis function（RBF）： 是一个取值仅取决于输入与某个固定点（一般为原点）之间的距离的函数
分类：RBF可以分为具有全局影响的RBF和具有局部影响的CSRBF（compactly-supported RBF紧密支持，仅在半径范围内非0）
应用：求解pde和构造神经网络都可以用的到

在确定RBF中的系数时涉及求解线性方程组的步骤

以下开始本文内容：

为IGA重用做准备，需要把模型分割成一系列和预定义的域一致的基本域，每个基本域用一个三元样条表示。
假设IGA的重用是应用在具有相似语义特征（semantic features）的模型上，也就是形状不同但拓扑相同；这些语义特征被指定为锚点，分析将遵循这些语义特征（目前好像基本都是由用户指定锚点）。

1. Consistent boundary surface decomposition 一致边界曲面分解

根据交叉参数化论文中的内容：可由用户指定或算法生成锚点，然后通常是通过追踪锚点间的最短路径来分割曲面。为了确保拓扑一致性，在追踪最短路径时需要满足三个条件： free of intersections, blocking, and wrong cyclical order（也是交叉参数化论文中的内容）。对模型曲面完成分割后，就可以按块把模型网格映射到模板基本域上。

2. CSRBF-based volumetric parameterization 基于CSRBF的体参数化

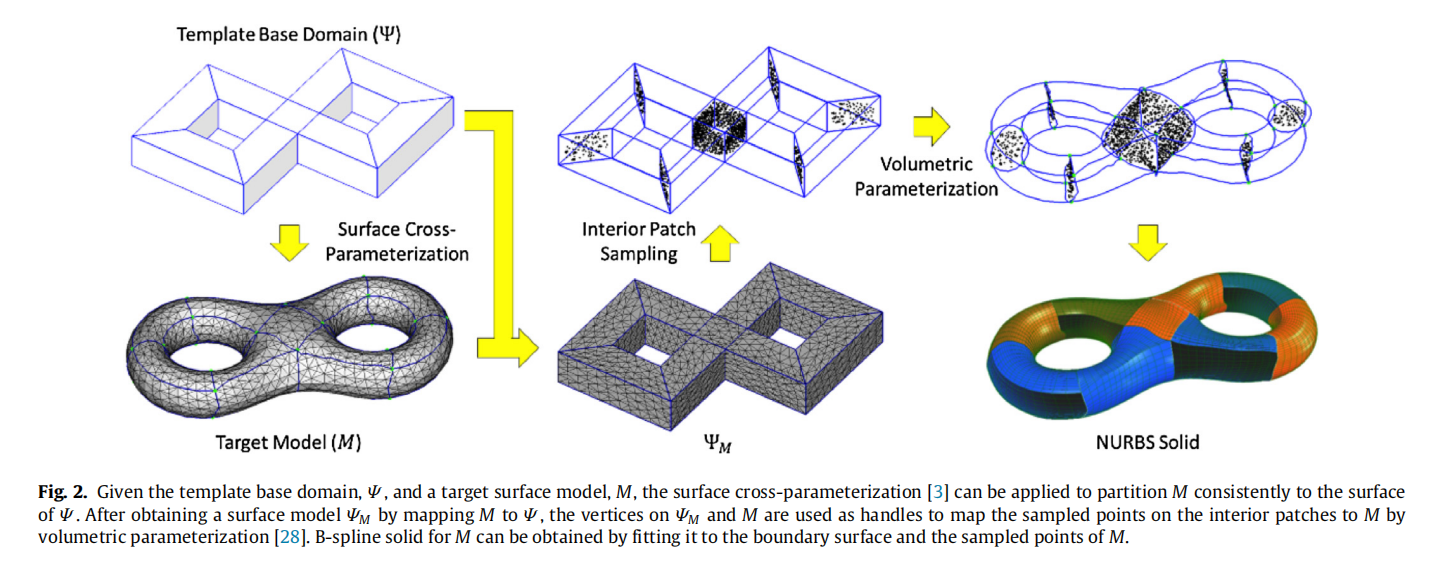
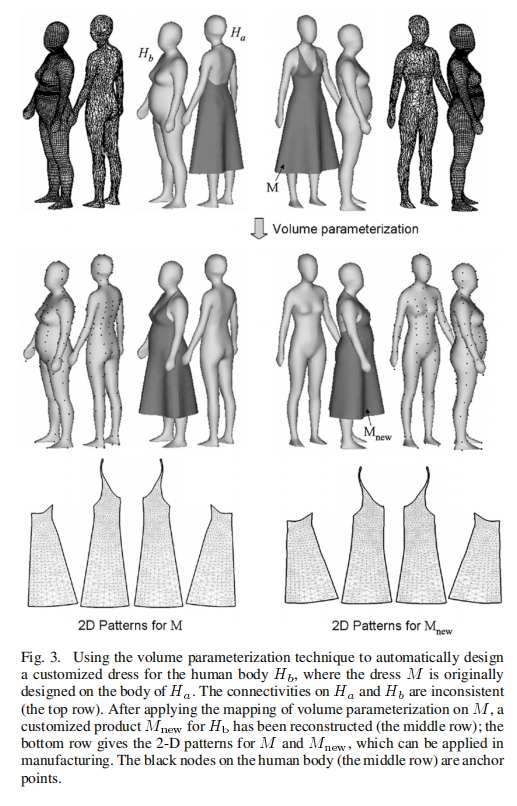
因为目标模型M是一个没有体信息的曲面模型，所以需要为M构造内部面片：先在模板基本域的内部面片中采样，然后再根据《Volume Parameterization for Design Automation of Customized Free-Form Products》中”基于CSRBF的弹性函数“的体参数化方法把这些采样点映射到目标模型M的内部。
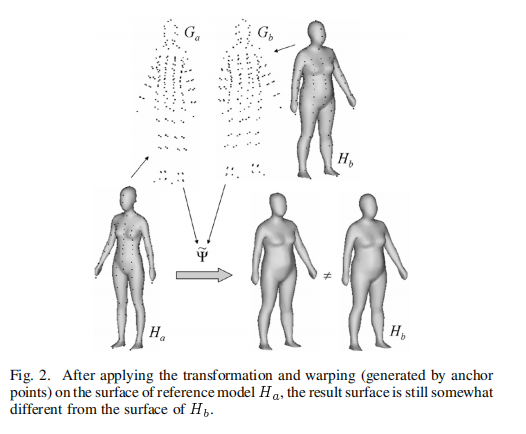
这篇论文《Volume Parameterization for Design Automation of Customized Free-Form Products》中的体参数化方法主要解决的问题是：根据锚点（最小二乘法）为两个模型建立一个映射，然后一个模型附近的一些点就可以映射到另一个模型上。
应用：比如一个模型穿的衣服可以迁移到另一个模型上。

这种方法在本篇论文中的应用：是为了把模板基本域内部面片上采样的点映射到目标模型M上
这个方法中的体参数化volumetric parameterization（这中叫法很奇怪，其实就是通过锚点得到的两个模型之间的映射）可以用下面这个弹性函数表示

这个函数中未知量有：权重dj和P(x)
函数f(x)实际表示的是两个模型之间的映射，所以我们可以根据模板基本域上的锚点v和目标模型M上的锚点v’得到下面的式子

可以构建一个线性方程组并求解出未知量dj，得到f(x)的具体表达形式
再用f(x)可以把模板基本域内部面片的采样点映射到目标模型M中

3. B-spline solid construction b样条实体构造

最后，可以通过拟合边界曲面和采样点为目标模型M的每一个基本域构造三元b样条实体，通过这种方式，就可以把M转换成和模板基本域拓扑一致的一组连接的三元样条实体。

二. Quadrature-free isogeometric analysis with Bézier extraction and polynomial approximation 通过bezier提取和多项式逼近的无积分等几何分析

关键词：bezier提取、多项式逼近、无积分
简单理解本块内容：通过bezier提取把b样条表示转化成beizer表示，并且用了bezier函数多项式逼近技术，避免了原先等几何分析中的数值积分过程，但分析过程和原先等几何分析的过程基本一致。

1. bernstein多项式基础知识

注意公式（5），bernstein的积分计算很简单，后面会利用这个性质

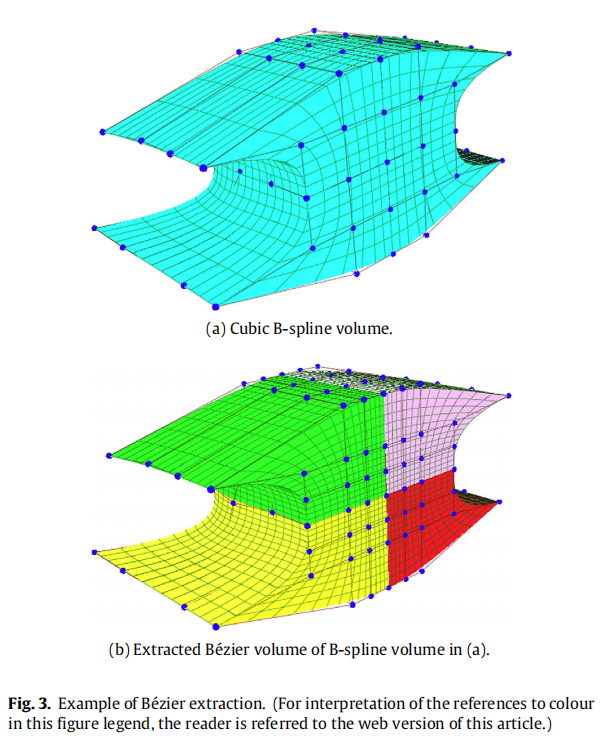
2. b样条体的bezier提取

为了达到有效的计算，应用bezier提取方法来解决等几何分析问题，需要将分段b样条表示转换成bezier表示。
不失一般性，在一个节点向量上定义的b样条基可以写作bernstein多项式的线性组合；根据公式（8）可以得到b样条体的表示转换，如公式（9）所示

具体的bezier提取部分的知识可以参考文献《Isogeometric finite element data structures based on Bézier extraction of NURBS》

3. 热传导问题的等几何分析

本小节用一个热传导的例子来梳理一遍本文提出的无积分等几何方法
给定一个模型，它的体参数化表示如下（以下的$B$应该都是bezier多项式，注意$B(x)$和$\widehat{B(u)}$的区别）：

在这个模型上求解如下的热传导问题：

根据经典的求解方法，经过变分法、分部积分、应用边界条件等一系列步骤，可以把这个热传导方程转化成下面的式子：

在IGA中，可以用基函数的线性组合表示解(这里的 $\widehat{B_i}$ 是bernstein多项式)：

在上面公式（11）中的$\psi (x)$被称为试函数，可取值如下：(物理域表示到参数域表示)

公式（11）的弱形式为：

得到一个线性系统：

接下来就是计算刚度矩阵的项$M_{ijk,rst}$

4. 刚度矩阵项的显示表示

1. 求解过程

假设刚度矩阵的项可表示如下：

经过推导（详细推导看论文），可以得到如下公式，用一个三元有理bezier函数表示F(u)：

接下来，根据参考论文《Approximating rational Bézier curves by constrained Bézier curves of arbitrary degree》中 weighted least-squares approach用一个三元多项式bezier函数G(u)来近似有理函数F(u)

这个bezier逼近问题可以转化成寻找权重$G_{ijk}$，使得G(u)成为F(u)的最佳逼近
F(u)可以写成这样的形式

寻找权重的问题可以转化成最小化下面这个式子：

经过推导计算，最终可以得到这样一个式子

其中变量如下：

求得G之后，可以得到通过bezier的积分化简求得刚度矩阵的项：

2. 提高结果精度的方法和IGA-Galerkin的三种方法类似

三. Computation-reuse for models with consistent volume parameterization 一致体参数化模型的计算重用

1. 计算重用框架

2. 刚度矩阵项的计算重用

在本文提出的框架中，主要有两个重用部分：单元刚度矩阵的项和边界条件的施加

单元刚度矩阵的项

由二.4可知，计算刚度矩阵的项的公式为：

其中G的计算公式如下：

这个公式中只有F的计算麻烦一些，其余变量基本都是和阶数有关（一致参数化后，基本域的阶数相同，这些量的计算应该也是重用的）
而F的计算公式如下：

在计算刚度矩阵的项的过程中，有三项计算是可重用的
（1）$F(u)$中的$J_{ijk}$

$J_{ijk}$的计算也只有部分即系数$D_{ijk}$可重用，因为它的计算和控制顶点有关，而每个模型的控制顶点的位置基本是不一样的
（2）$F(u)$中的$F_{ijk}$
$F_{ijk}$的计算可以看作三元bezier函数乘积的多次重复过程（文中没有细讲，应该跟定理4.4相关）
（3）逼近$F(u)$的$G(u)$的计算

逼近bezier的阶数(α, β, γ )和b样条模型的阶数(l, m, n) ，以及σ 、$L^{-1}$、Q都跟控制顶点的信息无关，所以它们的计算都是可重用的

施加边界条件

bernstein基函数在控制顶点上没有插值的性质，所以不能直接把初始边界条件施加在边界的控制变量上。需要用特殊的方法，比如最小二乘法、惩罚函数法或Nitsche法（不了解）
本篇论文用的方法是collocation(装配？)法：

对于一组有拓扑一致体参数化的计算模型，有相同的边界条件，在边界上的控制变量（以上求解出来的B）可以重用；对于不同的边界条件，collocation矩阵（以上公式中的$M^{-1}$）可以重用

今天的文章拓扑一致性是什么意思_一致连续的几何意义「建议收藏」分享到此就结束了，感谢您的阅读。