在上题目之前，先上我学的链式向前星！！！

存边的一种模式，我们之前一直是数组存边，但是当点过多的时候，数组就不行，于是我们就带入一种新的存边方式！！！

首先我们定义一个结构体和一个数组（来记录这个点出发的最后一条边的编号）以及一个记录第几条边

struct note { int to;//去哪里 int len;//边的权重 int next;//上一条这个点出去的边 }a[1000]; int frist[1000];//记录是第几条边 int cot;

然后我们应该怎么把边存进去呢，首先我们看到这个图

首先我们输入1 2 6，表示1是起点，2是终点，6是权重

我们发现1的上一条，没有于是就把0进入first【1】，和next，然后在把其他的存入，然后我们发现cot=1；就让first【1】=cot；

于是我们就可以得到

经过多次这样子的操作，我们就可以得到这样子的一张图

那我们就用代码来实现

struct note { int to; int len; int next; }a[1000]; int frist[1000]; int cot; void cunbian(int a,int b,int c)// { cot++; a[cot].len=c; a[cot].to=b; a[cot].next=frist[a]; frist[a]=cot; }

这样子我们就把这些边存进去了

可以看看【图的存储-轻松学习链式前向星】https://www.bilibili.com/video/BV1pDA?vd_source=c9016f395efdf6f1094ae706e81044e3

这个大佬的讲解，很清楚！！！

# 【模板】单源最短路径（弱化版）

题目背景

本题测试数据为随机数据，在考试中可能会出现构造数据让SPFA不通过，如有需要请移步 [P4779](https://www.luogu.org/problemnew/show/P4779)。

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入格式

第一行包含三个整数 $n,m,s$，分别表示点的个数、有向边的个数、出发点的编号。

接下来 $m$ 行每行包含三个整数 $u,v,w$，表示一条 $u \to v$ 的，长度为 $w$ 的边。

输出格式

输出一行 $n$ 个整数，第 $i$ 个表示 $s$ 到第 $i$ 个点的最短路径，若不能到达则输出 $2^{31}-1$。

样例 #1

样例输入 #1

```

4 6 1

1 2 2

2 3 2

2 4 1

1 3 5

3 4 3

1 4 4

```

样例输出 #1

```

0 2 4 3

```

提示

【数据范围】

对于 $20\%$ 的数据：$1\le n \le 5$，$1\le m \le 15$；

对于 $40\%$ 的数据：$1\le n \le 100$，$1\le m \le 10^4$；

对于 $70\%$ 的数据：$1\le n \le 1000$，$1\le m \le 10^5$；

对于 $100\%$ 的数据：$1 \le n \le 10^4$，$1\le m \le 5\times 10^5$，$1\le u,v\le n$，$w\ge 0$，$\sum w< 2^{31}$，保证数据随机。

Update 2022/07/29：两个点之间可能有多条边，敬请注意。

对于真正 $100\%$ 的数据，请移步 [P4779](https://www.luogu.org/problemnew/show/P4779)。请注意，该题与本题数据范围略有不同。

样例说明：


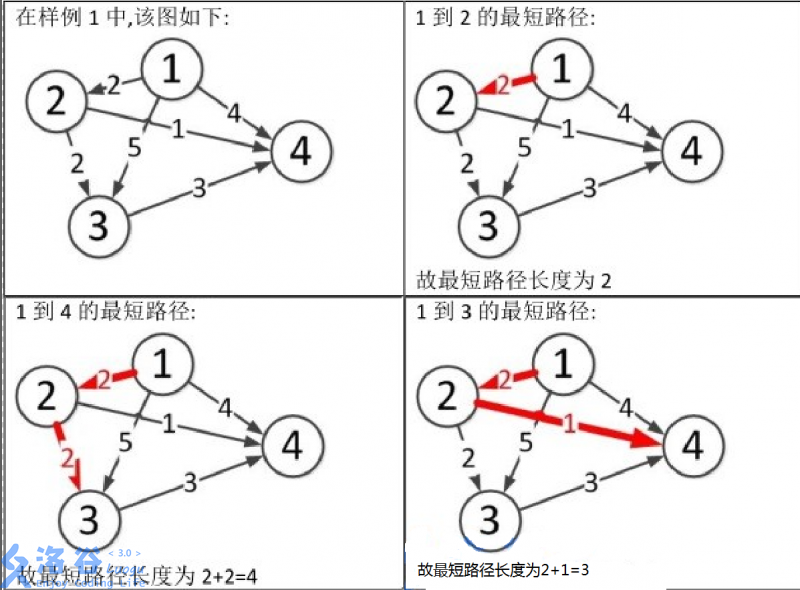
图片1到3和1到4的文字位置调换

就是求最短路，不会的小伙伴可以看看我前天那个最短路

#include <stdio.h> int frist[];//出现的最后一个边 int cot; int max=; struct lian { int to;//表示去哪里 int len;//长度 int next;//表示上一条边 }eadg[]; void cunbian(int u,int v,int w) { cot++; eadg[cot].to=v; eadg[cot].len=w; eadg[cot].next=frist[u]; frist[u]=cot; } int p[],t[];//p表示距离，t表示是否用过 int main() { int i,maxx; int n,m,s; int u,v,w; scanf("%d%d%d",&n,&m,&s);//x表示起点 for(i=1;i<=m;i++) { scanf("%d%d%d",&u,&v,&w); cunbian(u,v,w); } for(i=1;i<=n;i++) { p[i]=max; } p[s]=0; while(!t[s]) { t[s]=1;//表示被记录起点 for(i=frist[s];i!=0;i=eadg[i].next)//把起点到下一个点的位置出发 { if(!t[eadg[i].to]&&p[eadg[i].to]>p[s]+eadg[i].len) { p[eadg[i].to]=p[s]+eadg[i].len; } } maxx=max; for(i=1;i<=n;i++)//找最小的那个p，然后从最小的哪里出发 { if(!t[i]&&maxx>p[i]) { maxx=p[i]; s=i; } } } for(i=1;i<=n;i++) { printf("%d ",p[i]); } }

本来是还有一个标准版，可是可是堆优化我还没学，咱就看看下一个题目吧

# 邮递员送信

题目描述

有一个邮递员要送东西，邮局在节点 $1$。他总共要送 $n-1$ 样东西，其目的地分别是节点 $2$ 到节点 $n$。由于这个城市的交通比较繁忙，因此所有的道路都是单行的，共有 $m$ 条道路。这个邮递员每次只能带一样东西，并且运送每件物品过后必须返回邮局。求送完这 $n-1$ 样东西并且最终回到邮局最少需要的时间。

输入格式

第一行包括两个整数，$n$ 和 $m$，表示城市的节点数量和道路数量。

第二行到第 $(m+1)$ 行，每行三个整数，$u,v,w$，表示从 $u$ 到 $v$ 有一条通过时间为 $w$ 的道路。

输出格式

输出仅一行，包含一个整数，为最少需要的时间。

样例 #1

样例输入 #1

```

5 10

2 3 5

1 5 5

3 5 6

1 2 8

1 3 8

5 3 4

4 1 8

4 5 3

3 5 6

5 4 2

```

样例输出 #1

```

83

```

提示

对于 $30\%$ 的数据，$1 \leq n \leq 200$。

对于 $100\%$ 的数据，$1 \leq n \leq 10^3$，$1 \leq m \leq 10^5$，$1\leq u,v \leq n$，$1 \leq w \leq 10^4$，输入保证任意两点都能互相到达。

这个题目就是单源最短换成了，多源最短，但是如果我们要那样子想求单源最短的方法来，那就错错错！！！我们可以想一下，我们去是单源最短，我们回来就又可以把那个图翻转过来，变成单源最短问题，不就ok了噻

#include <stdio.h> int a[1001][1001],dis[1001],t[1001]; const int max=; void chu(int n) { int i,j; for(i=1;i<=n;i++) { for(j=1;j<=n;j++) { if(i!=j) a[i][j]=max; } } } void dij(int n) { int i,j,min; t[1]=1; int s; for(i=1;i<n;i++) { min=max; for(j=1;j<=n;j++) { if(!t[j]&&min>dis[j]) { min=dis[j]; s=j; } } t[s]=1; for(j=1;j<=n;j++) { if(!t[j]&&a[s][j]+dis[s]<dis[j]) { dis[j]=a[s][j]+dis[s]; } } } } void fanzhuan(int n) { int teap,i,j; for(i=1;i<=n;i++) { for(j=i+1;j<=n;j++) { teap=a[i][j]; a[i][j]=a[j][i]; a[j][i]=teap; } } } int main() { int n,m,x,y,z,i,j; scanf("%d%d",&n,&m); chu(n); for(i=1;i<=m;i++) { scanf("%d%d%d",&x,&y,&z); if(z<a[x][y]) { a[x][y]=z; } } for(i=1;i<=n;i++) { dis[i]=a[1][i]; t[i]=0; } dij(n); long long sum=0; for(i=1;i<=n;i++) { sum=sum+dis[i]; } fanzhuan(n); for(i=1;i<=n;i++) { dis[i]=a[1][i]; t[i]=0; } dij(n); for(i=1;i<=n;i++) { sum=sum+dis[i]; } printf("%lld",sum); }

okok下班下班