一、常用的离散型随机变量及其概率分布
1、(0-1)分布(伯努利分布(Bernoulli distribution)、两点分布)
如果随机变量X 只可能取0与1两个值,其概率分布为:
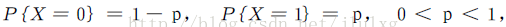
或写成
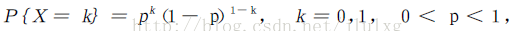
则称随机变量X 服从(0-1)分布或两点分布.它的概率分布也可以写成

2、二项分布
在n重伯努利试验中,如果以X表示事件A 出现的次数,则X是一个离散型随机变量,它的所有可
能取值是0,1,2,⋯,n.设P(A)= p(0< p<1)。典型例子是扔硬币,硬币正面朝上概率为p, 重复扔n次硬币,k次为正面的概率即为一个二项分布概率。概率函数为

显然,

3、多项式分布
把二项分布公式再推广,就得到了多项分布。比如扔骰子,不同于扔硬币,骰子有6个面对应6个不
同的点数,这样单次每个点数朝上的概率都是1/6(对应p1~p6,它们的值不一定都是1/6,只要和为1且
互斥即可,比如一个形状不规则的骰子),重复扔n次,如果问有x次都是点数6朝上的概率就是:

4、几何分布
设试验E只有两个可能的对立的结果A 及A非,并且P(A)= p,P(A非)=1- p,其中0< p<1.将试验E独立地重复进行下去,直到事件A发生为止.如果以X表示所需要的试验次数,则X是一个随机变量,它可能取的值是1,2,3,⋯.由于事件{X = k}表示前k-1次试验中事件A都没有发生,而在第k次试验中事件A 发生,因此
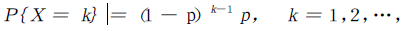
我们称随机变量X 服从几何分布。
5、泊松分布
设随机变量X 的所有可能取值为0,1,2,⋯,并且
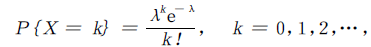
其中λ>0是常数,则称随机变量X服从参数为λ的泊松分布,记作X~π(λ).易知
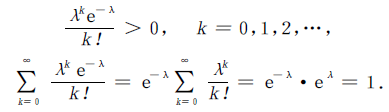
在实际问题中经常会遇到服从泊松分布的随机变量.例如,在一个长为τ的时间间隔内某电话交换台收到的电话呼叫次数;某医院在一天内来急诊的病人数;某一本书的一页中的印刷错误数等都服从泊松分布.
二、连续型随机变量及其概率密度
1、均匀分布
设连续型随机变量X 的概率密度为:
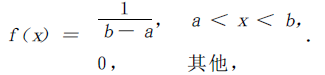
则称X在区间[a,b]上服从均匀分布.X 的分布函数为
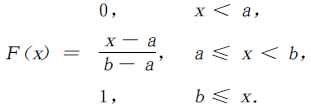
X的概率密度和分布函数的图形分别如图所示:
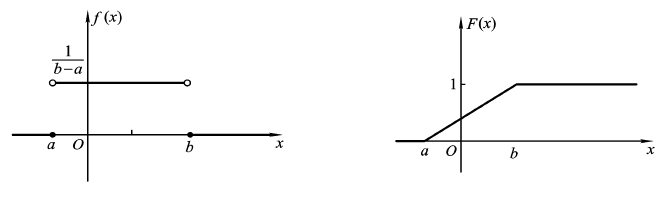
2、指数分布
设连续型随机变量X 具有概率密度
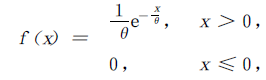
其中θ>0是常数,则称X服从参数为θ的指数分布.X的分布函数为
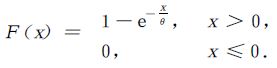
X的概率密度及分布函数的图形分别如图所示:
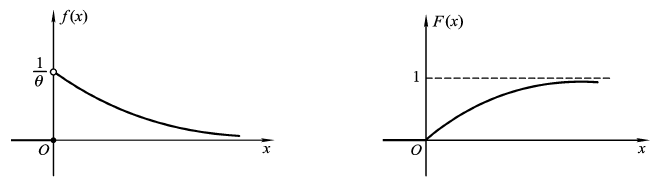
实际问题中的许多随机变量,例如电子元件的寿命,旅客在车站售票处购买车票需要等待的时间等都可以看成是服从指数分布。
3、正态分布
设随机变量X 具有概率密度
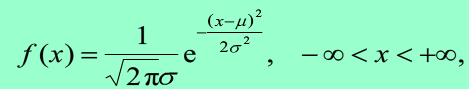
其中μ,σ(σ>0)为常数,则称X服从参数为μ,σ的正态分布,记作X~ N(μ,σ2).X的分布函数为
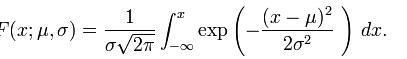
它们的图形分别如图所示:
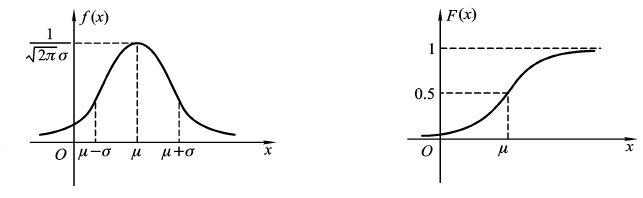
容易看到概率密度曲线y= f(x)关于直线x= μ对称,并在x= μ处取得最大值 ,在横坐标x= μ± σ处有拐点,以x轴为水平渐近线.
,在横坐标x= μ± σ处有拐点,以x轴为水平渐近线.
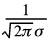 ,在横坐标x= μ± σ处有拐点,以x轴为水平渐近线.
,在横坐标x= μ± σ处有拐点,以x轴为水平渐近线.
如果μ=0,σ=1,则称X服从标准正态分布,记作X~N(0,1).它的概率密度及分布函数分别记作φ(x)与Φ(x),即
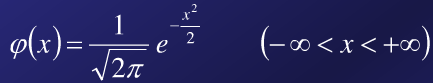
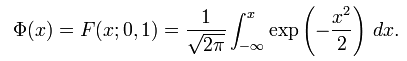
参考资料:随机数学 吉林大学数学学院 高文森,潘伟 主编

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/108301.html